用位运算实现四则运算
四则运算的位运算实现
以C语言为例由位运算实现四则运算
位运算简单介绍
加法运算
12+89=101
将上述加法运算分解为如下过程
步骤1:不考虑进位的运算 12+88 = 01,转到步骤2
步骤2:仅考虑进位的运算 12+88 = 100,转到步骤3
步骤3:如果仅考虑进位的运算结果不为0,将两次运算的结果作为加数,重复步骤1
以二进制考虑
0000 1100 + 0101 1001 = 0110 0101
不考虑进位的运算 0000 1100 + 0101 1001 = 0101 0101
仅考虑进位的运算 0000 1100 + 0101 1001 = 0001 0000
将上述结果相加 0101 0101 + 0001 0000
不考虑进位的运算 0101 0101 + 0001 0000 = 0100 0101
仅考虑进位的运算 0101 1001 + 0001 0000 = 0010 0000
将上述结果相加 0100 0101 + 0010 0000
不考虑进位的运算 0100 0101 + 0010 0000 = 0110 0101
仅考虑进位的运算 0100 0101 + 0010 0000 = 0000 0000
终止
结果为 0110 0101
观察可知,不考虑进位的运算即是异或,仅考虑进位的运算即是与运算再左移一位
那么加法可以写作
int add(int sum, int carry){
if(carry==0)return sum;
return add(sum ^ carry, (sum & carry)<<1);
}
或者
int add(int a, int b){
int sum, carry;
do{
sum = a ^ b;
carry = (a & b)<<1;
a = sum;
b = carry;
}while(carry);
return sum;
}
上述操作步骤上就是机器实现加法运算的过程
减法运算
学习计算机基础后,我们应该知道,计算机中使用补码来表示数值
正数的原码、反码与补码相同
负数将原码除符号位取反后得到反码,反码加1得到补码
一个数加上另一个数的补码即相当于减去这个数
不难得到
int minus(int num, int dead){
return add(num,add(~dead,1));
}
乘法运算
用加法实现乘法
首先
int abs(int num){
return num<0?add((~num),1):num;
}
然后
int multiply(int a, int b){
if(a==0||b==0)return 0;
int flag_a = (a>>31)&1;
int flag_b = (b>>31)&1;//取符号位
a = abs(a);
b = abs(b);//计算绝对值
int min = a>b?b:a;
int max = a>b?a:b;
int res = 0;
while(min){
min = minus(min,-1);
res = add(res,max);
}//用加法实现乘法
if(flag_a!=flag_b){
res = add((~res),1);
}//判断符号
return res;
}
优化
上述思路选取小值作为加法次数
但是加上成千上万次还是太多了
实际上 如下图
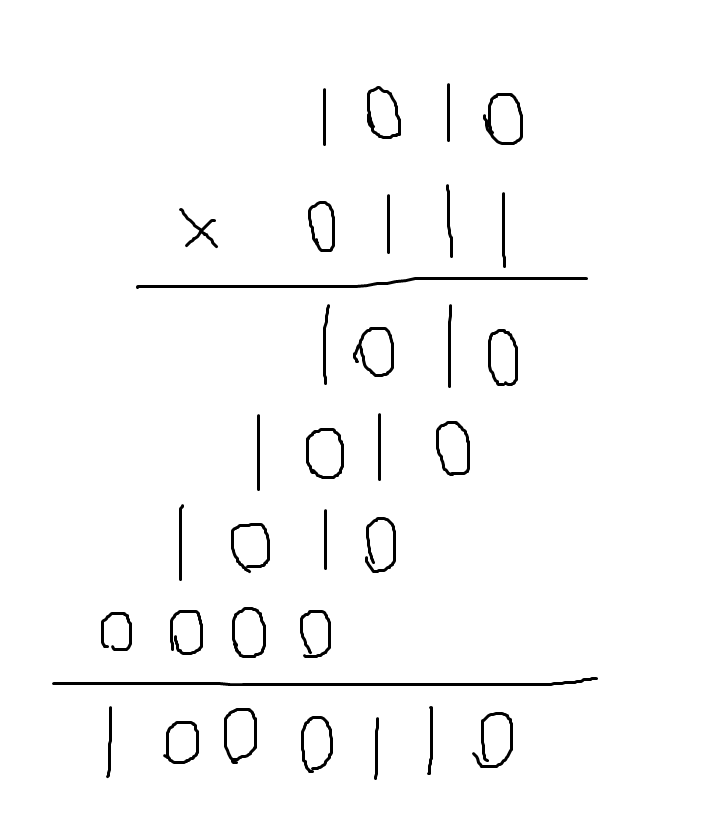
借助取位操作与左移操作
只需将左移过的三个1010相加即可
也就是说 对于32位的int来说 最多做31次加法就足够了
int multiply(int a, int b){
if(a==0||b==0)return 0;
int flag_a = (a>>31)&1;
int flag_b = (b>>31)&1;
a = abs(a);
b = abs(b);
int res = 0;
int cnt = 0;//位数
while(cnt<32){
if(a&1){//取最后一位判断
res = add(res,b<<cnt);
}
a = a>>1;//a右移 舍弃乘过的一位
cnt = add(cnt,1);
}
if(flag_a!=flag_b){
res = add((~res),1);
}
return res;
}
除法运算
同样的思路,用减法实现除法
int devide(int num, int dev){
int flag = ((num ^ dev)<0);
// if(dev==0)return flag; 不做除零处理
num = abs(num);
dev = abs(dev);
int cnt = 0;
while(num>=dev){
num = minus(num, dev);
cnt = add(cnt, 1);
}
if(flag){
cnt = (~cnt) + 1;
}
return cnt;
}
优化
每次减去一个被除数,可不可以一次减去多个被除数呢
如下
int devide(int num, int dev){
int cnt = 0;
int flag = (num^dev)<0;
num = abs(num);
dev = abs(dev);
for(int i = 31;i>=1;i=add(i,1)){
while((num>>i)>=dev){//num 大于 dev乘以2的i次方 避免越界所以用num>>i
num = minus(num,dev<<i);
cnt = add(cnt, 1<<i);
}
if(num<dev){
break;
}
}
if(flag){
cnt = add((~cnt),1);
}
return cnt;
}
用优化过的除法用99999999除以1,用了4s+。。。
好难过。。于是我又加了除数为1的判断
2019/4/14




