像计算机科学家一样思考python-第4章 案例研究:接口设计
系统环境 ubuntu18
4.1turtle模块
模块一开始导入turtle模块就报错了
1 Python 3.6.5 (default, Apr 1 2018, 05:46:30) 2 [GCC 7.3.0] on linux 3 Type "help", "copyright", "credits" or "license" for more information. 4 >>> import turtle 5 Traceback (most recent call last): 6 File "<stdin>", line 1, in <module> 7 File "/usr/lib/python3.6/turtle.py", line 107, in <module> 8 import tkinter as TK 9 ModuleNotFoundError: No module named 'tkinter'
从错误信息中可以看出:
turtle模块引用tkinter模块,但当前的运行环境没有tkinter模块文件,所以报错
解决办法:
注意:这里如果直接安装tkinter,会发现没有tkinter包
因为python-tk/python3-tk的类库需要在操作系统层面进行安装
这里把tkinter是什么,以及解决的过程描述的很清晰了。不再缀述,
Python3下提示No module named 'tkinter'"问题解决
只说解决办法:
ubuntu16.04导入 pyplot报错:ModuleNotFoundError: No module named 'tkinter'
使用命令安装:
sudo apt-get install tcl-dev tk-dev python3-tk
开始安装:
1 wangju@wangju-GL553VD:~$ sudo apt-get install tcl-dev tk-dev python3-tk 2 [sudo] password for wangju: 3 Reading package lists... Done 4 Building dependency tree 5 Reading state information... Done
完成安装:
再试一下:
问题解决
1 Python 3.6.5 (default, Apr 1 2018, 05:46:30) 2 [GCC 7.3.0] on linux 3 Type "help", "copyright", "credits" or "license" for more information. 4 >>> import turtle 5 >>> bob = turtle.Turtle()
出现了一个这样的窗口

创建文件mypolygon.py
代码如下:
1 import tutle 2 bob = turtle.Turtle() 3 print(bob) 4 turtle.mainloop()
运行mypolygon.py,结果如下:
1 wangju@wangju-GL53VD:~$ python3 mypolygon.py 2 <turtle.Turtle object at 0x7f44a642da58>
若要画一个朝右的角,在程序中(建立bob实例之后,调用mainloop之前)添加如下代码:
bob.fd(100) bob.lt(90) bob.fd(100)
运行这个程序时,将会看到bob先向东走,再向北走,身后留下两线段
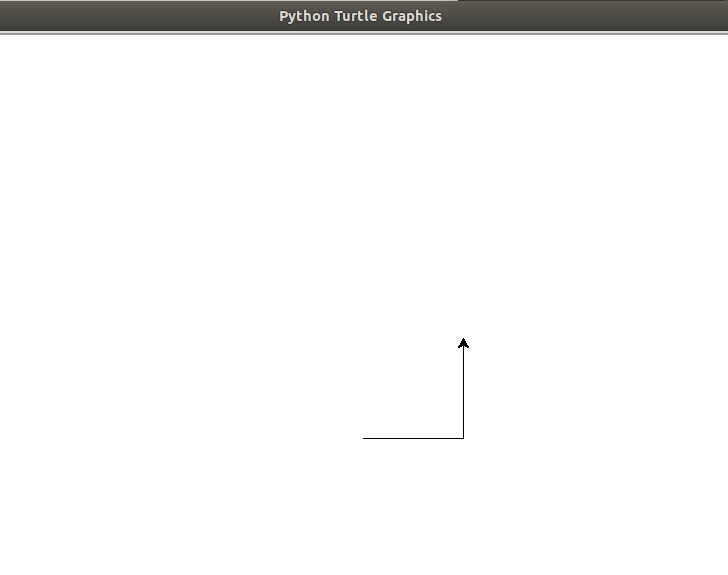
现在修改程序,画出一个正方形来
1 bob.fd(100) 2 bob.lt(90) 3 4 bob.fd(100) 5 bob.lt(90) 6 7 bob.fd(100) 8 bob.lt(90) 9 10 bob.fd(100)
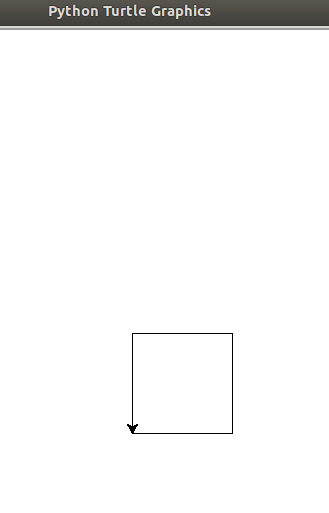
4.2简单重复
下面是使用for语句绘制正方形的程序
1 for i in range(4): 2 bob.fd(100) 3 bob.lt(90)
for 语句的语法和函数定义类似。它也有一个以冒号结束的语句头,并有一个缩进的语句体。语句体可以包含任意数量的语句。
for语句也称为循环(loop),因为执行流程会遍历语句体,之后从语句体的最开头重新循环执行。在这个例子里,,语句体执行了4次。
4.3练习
1.写一个函数 square,接受一个形参t,用来表示一只乌龟。利用乌龟来画一个正方形。
写一个函数调用,传入bob作为实参来调用square函数,并再运行一遍程序。
1 import turtle 2 bob = turtle.Turtle() 3 4 def square(t): 5 for i in range(4): 6 t.fd(100) 7 t.lt(90) 8 9 #函数调用 10 square(bob) 11 turtle.mainloop()
2.给 square 函数再添加一个形参 length。修改函数内容,保证正方形的长度是length,并修改函数调用以提供这第二个实参。再运行一遍程序。使用不同的length值测试你的程序。
1 import turtle 2 bob = turtle.Turtle() 3 4 def square(t,length): 5 for i in range(4): 6 t.fd(length) 7 t.lt(90) 8 9 square(bob,50) 10 turtle.mainloop()

3.复制 square函数,并命名为 polygon。再添加一个形参n并修改函数体以绘制一个正n边形。提示: 正n边形的拐角是360/n度。
def polygon(t,length,n): '''t bob,length 多边形每边的长度(bob每次移动的距离),n 正n边形''' for i in range(n): t.fd(length) t.lt(360/n) # square(bob,200) #正五边形 # polygon(bob,100,5) #正3角形 polygon(bob,100,3)

4.写一个函数 circle接受代表乌龟的形参t,以及表示半径的形参 r ,并使用合适的长度和边数调用polygon画一个近似的圆。使用不同的r 值来测试你的函数。
提示: 思考圆的周长(circumference),并保证 length * n = circumference.
另一个提示: 如果你觉得bob太慢,可以修改bob.delay来加速。bob.delay代表每次行动之间的停顿,单位是秒。bob.delay = 0.01应该能让它跑得足够快。
解释:bob第一次移动的距离即圆形的半径r(圆上的任意一点到圆心的距离称为半径)。如图所示:
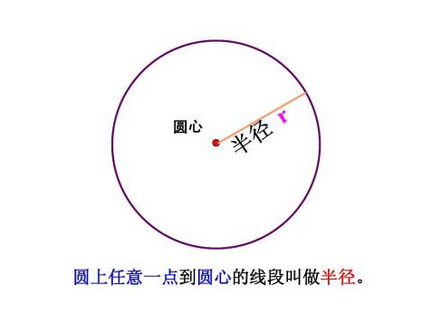
圆的周长公式:周长L=2πr(其中r为圆的半径,π为圆周率,通常情况下取3.14)
所以“ 合适的长度和边数”是
length * n = circumference
而
circumference=2πr
所以 length * n=2πr
如果不遵守这个规则,也可以画出圆,但是圆的半径却不能保证是r了,如图:

缩小r的值以后:

使用函数来编写程序:
1 def circle(t,r,length,n): 2 #先画出圆心到圆周的距离r 3 t.fd(r) 4 polygon(t,length,n) 5 6 #半径100 7 circle(bob,100,12.5,50)

5.给circle函数写一个更通用的版本,称为arc。增加一个形参 angle,用来表示画的圆弧的大小。这里angle的单位是度数,所以当 arc = 360时,则会画一个整圆。
这道题看不太懂是什么意思,我想是不是应该是这个意思,指定一个圆的周长,用angle表示。然后当周长是360时,会画出一个整圆(应该是angle=350吧?)
1 #angle 表示圆弧的长度 2 def arc(t,angle): 3 #随机生成一个在10~30之间的边长 4 n = random.randint(15,20) 5 6 length= angle/n 7 8 t.fd(n) 9 polygon(t,length,n) 10 arc(bob,360)

最后一道题感觉做的有问题,但是不想再深究了,因为主要不是为了解析这一道数学题目,而是为了学习书中的编程思想
4.4 封装
第一个练习要求把画正方形的代码放到一个函数定义中,并将乌龟bob作为实参传入,调用该函数。
最内侧的语句,fd和lt都缩进了两层,表示它们是在for 语句体内部,而for语句在函数定义的函数体内部。最后一行 square(bob),又重新从左侧开始而没有缩进,这表明for语句和square函数都已经结束。
在函数体中,t引用的乌龟和bob引用的相同,所以 t.lt(90)和直接调用bob.lt(90)是一样的效果。在这种情况下为什么不直接把形参写成bob呢?原因是t可以是任何乌龟,而不仅仅是bob,所以可以再新建一只乌龟,并将它作为参数传入到square函数
1 alice = turtle.Turtle() 2 square(alice)
把一段代码用函数包裹起来,称为封装。封装的一个好处是,它给这段代码一个有意义的名称,增加了可读性。另一个好处是,当重复使用这段代码时,调用一次函数比复制粘贴代码要简易的多。
4.5泛化
给函数添加参数的过程称为泛化,因为它会让函数变得更通用
如果函数的形参比较多,很容易忘掉每一个具体是什么,或者忘掉它们的顺序,所以在Python中,调用函数时可以加上形参名称,这样是合法的,并且有时候会有帮助:
polygon(bob,n=7,length=70)设计
4.6接口设计
函数的接口是如何使用它的概要说明:它有哪些参数?这个函数做什么?它的返回值是什么?我们说一个接口“整洁”,是说它能够让调用者完成所想的的事情,而不需要处理多余的细节
在这个例子里,r属于函数的接口,因为它指定了所画的圆的基本属性。相对地,n则不那么适合,因为它说明的是如何画圆的细节信息。
所以与其弄乱接口,不如在代码内部根据周长来选择合适的n值
1 def circle(t,r): 2 circum=2*math.pi*r 3 n=int(circum/3)+1 4 length=circum/n 5 length= circum/n 6 polygon(t,n,length)
现在多边形是的边数是一个接近circum/3的整数,所以每个边长近似是3,已经小到足够画出好看的圆形,但又足够大到不影响画线效率,并且可接受任何尺寸的圆。
关于圆形练习题,书中的答案:
1 import turtle 2 import math 3 bob = turtle.Turtle() 4 5 def polygon(t,n,length): 6 angle=360/n 7 for i in range(n): 8 t.fd(length) 9 t.lt(angle) 10 11 #version1 12 def circle(t,r): 13 circum=2*math.pi*r 14 n=50 15 length= circum/n 16 polygon(t,n,length) 17 18 #version2 19 def circle(t,r): 20 circum=2*math.pi*r 21 n=int(circum/3)+1 22 length=circum/n 23 length= circum/n 24 polygon(t,n,length) 25 26 circle(bob,150) 27 turtle.mainloop()
4.8一个开发计划
开发计划是一个写程序的过程。本章的案例分析中,我们使用的过程是“封装和泛化”。这个过程的具体步骤是:
1. 最开始写一些小程序,而不需要函数定义
2. 一旦程序运行成功,识别出其中一段完整的部分,将它封装到一个函数中,并加以命名。
3. 泛化这个函数,添加合适的形参。
4.重复步骤1到步骤3,直到得到一组可行的函数。复制粘贴代码,以避免重复输入(以及重复调试)
5.寻找可以使用重构来改善程序的机会。例如,如果发现程序中几处有相似的代码,可以考虑将它们抽取出来做一个合适的通用函数。
这个过程也有一些缺点——我们会在后面看到其他方式——但如果在开始编程时不清楚如何将程序分成适合的函数,这样做会带来帮助。这个方法能让你一边开发一边设计。
4.9文档字符串
文档字符串很简洁,但已经包含了其他人需要知道的关于函数的基本信息。它简明地解释了函数是做什么的(而不涉及如何实现的细节)。它解释了每个形参对函数行为的影响效果以及每个形参应有的类型(如果其类型并不显而易见)
编写这类文档是接口设计的重要部分。一个设计良好的接口,也应当很简单就能解释清楚; 如果你发现解释一个函数很困难,很可能表示该接口有改进的空间。
4.10调试
函数的接口,作用就像是函数和调用者之间签订的一个合同。调用者同意提供某些参数,而函数则同意使用这些参数做某种工作。
例如,polyline需要4个参数:t必须是一个Turtle; n必须是整数; length应当是个正数; 而则必须是一个数字,并且按照度数来理解。
这些需求被称为前置条件,因为它们应当在函数开始执行之前就保证为真。相对地,函数结束的时候需要满足的条件为后置条件。后置条件包含了函数预期的效果(如画出线段)以及任何副作用(如移动乌龟或者引起其他改变)
满足前置条件是调用者的职责。如果调用者违反了一个(文档说明清晰的!)前置条件,因而导致函数没有正确运行,则bug是在调用者,而不在函数本身。
如果前置条件都已经满足,但后置条件没有满足,那么bug就出现在函数本身。如果前置条件和后置条件都定义清晰,可以帮助调试。





