LeetCode 312. Burst Balloons
原题链接:https://leetcode.com/problems/burst-balloons/
这是一道比较复杂的动态规划问题,关键在于定义好独立的子问题。
原问题可以转化为求f(i, j)的最大值,当i == 0 && j == n时,就是我们要的答案。
把j逐次向后移动,依次求f(0, 1), f(0, 2)... f(0, n)的最大值。
求f(0, j)的最大值,可以转化为子问题:在0..j中找到元素k,当k是最后一个戳破时,f(1, k-1) + f(k+1, j) + num[0] * num[k] * num[j+1]值最大。
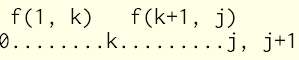
更进一步的思考:
1. 为什么最后一定是num[0] * num[k] * num[j+1]?如果是num[i]*num[k]*num[j+1]构成最大呢?其实这种情况已经被k = i-1这种case考虑过了:

2. 怎样找到max(f(1, k-1) + f(k+1, j) + num[0] * num[k] * num[j+1])?
我们可以令i = j-1..1,然后让k = j..i+1,找到使得f(i,j) = f(i+1, k-1) + f(k+1, j) + num[i] * num[k] * num[j + 1] 最大的k。因为i是从j-1向1移动的,所以每次可以利用前一轮计算的结果,也就是说f(i+1, k-1) 和 f(k+1, j)其实之前已经计算过。
因为每次j移动时,会对之前的乘积造成影响,所以需要重新计算一遍f(i, j)。
代码如下:
1 class Solution { 2 public: 3 int maxCoins(vector<int>& nums) { 4 if(nums.size() == 0){ 5 return 0; 6 } 7 if(nums.size() == 1){ 8 return nums[0]; 9 } 10 11 int size = nums.size(); 12 nums.push_back(1); 13 nums.insert(nums.begin(), 1); 14 vector<vector<int>> mem(size + 1, vector<int>(size + 1, 0)); 15 mem[1][1] = nums[1]*nums[2]; 16 mem[size][size] = nums[size-1]*nums[size]; 17 for(int i = 2; i < size; i++){ 18 mem[i][i] = nums[i-1]*nums[i]*nums[i+1]; 19 } 20 for(int j = 2; j <= size; j++){ 21 for(int i = j - 1; i >=1; i--){ 22 for(int k = j; k >= i; k--){ 23 int product = nums[k] * nums[i-1] * nums[j+1]; 24 int left = i < k ? mem[i][k-1]:0; 25 int right = j > k? mem[k+1][j]:0; 26 int sum = product + left + right; 27 mem[i][j] = max(sum, mem[i][j]); 28 } 29 } 30 } 31 32 return mem[1][size]; 33 } 34 };




【推荐】还在用 ECharts 开发大屏?试试这款永久免费的开源 BI 工具!
【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步