算法 回溯算法套路模板

回溯算法应用

经典的全排列和N皇后

 

怎么穷举全排列的呢？比方说给三个不重复数 [1,2,3]，你肯定不会无规律地乱穷举，一般是这样：

先固定第一位为 1，然后第二位可以是 2，那么第三位只能是 3；然后可以把第二位变成 3，第三位就只能是 2 了；然后就只能变化第一位，变成 2，然后再穷举后两位……

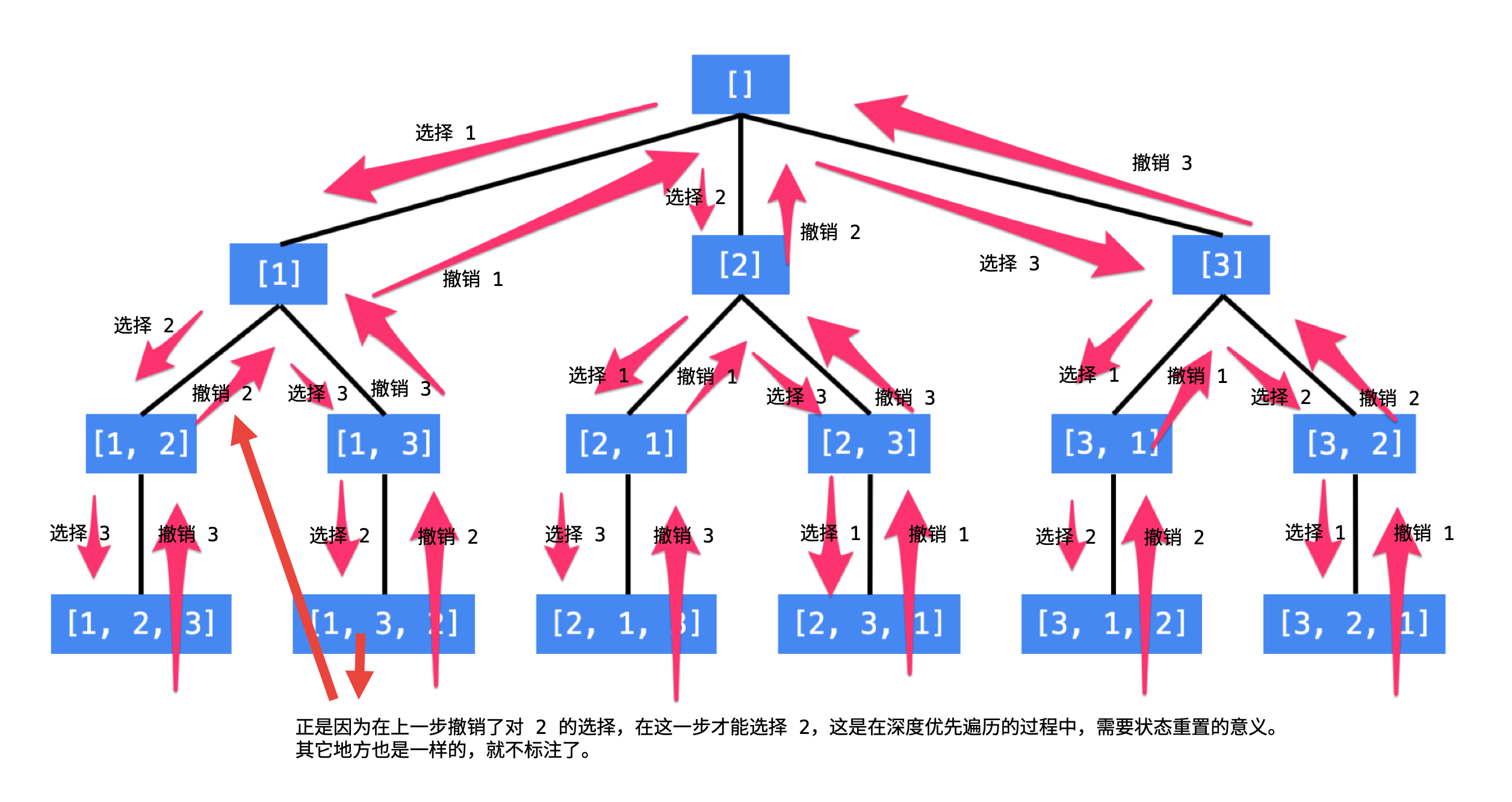
其实这就是回溯算法，只要从根遍历这棵树，记录路径上的数字，其实就是所有的全排列。我们不妨把这棵树称为回溯算法的「决策树」

为啥说这是决策树呢，因为你在每个节点上其实都在做决策，比如当前在树的第二层深度，站在数字2的位置做决策，可以选择 1 那条树枝，也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢？因为 2 这个树枝在你身后，这个选择你之前做过了，而全排列是不允许重复使用数字的

「路径」，记录你已经做过的选择；

「选择列表」就是[1,3] ，表示你当前可以做出的选择；可以通过状态数组来维护每一个深度下的状态

「结束条件」就是遍历到树的底层（或者判断所有的数都进入了路径中）

 

盗图显示（多谢原作者）：

 

 

 

代码块：

/// <summary>
/// 回溯法 递归 树形结构
/// 每次做选择，递归，然后回溯到上一层修改选择,满足条件后添加到结果列表（注意这里不同语法可能需要拷贝操作）
/// 其全排列的形成靠的是递归函数遍历到对应深度层， 另外的排列可能性在于回溯原来的状态以新的值作为递归的根
///
/// </summary>
/// <param name="nums"></param>
/// <returns></returns>
public IList<IList<int>> Permute(int[] nums)
{
IList<IList<int>> ans = new List<IList<int>>();
if (null == nums || nums.Length == 0) return ans;

bool[] marked = new bool[nums.Length];
backtrack_state(nums, marked, new List<int>(), ans);

return ans;
}

 

/// <summary>
/// 使用状态标记，空间换时间
/// </summary>
/// <param name="nums"></param>
/// <param name="path"></param>
/// <param name="ans"></param>
public void backtrack_state(int[] nums, bool[] marked, List<int> path, IList<IList<int>> ans)
{
// 有效路径
if (path.Count == nums.Length)
{
ans.Add(new List<int>(path)); // 拷贝操作，因为path再回溯上层会做修改
return;
}

for (int i = 0; i < nums.Length; i++)
{
// 其实可以用状态来标记的，但是会占用空间复杂度
if (marked[i]) continue;

marked[i] = true;
// 做选择
path.Add(nums[i]);

// 进入下一层决策树,递归下去
backtrack_state(nums, path, ans);

// 取消选择,,移除最后选择的路点，本层撤销后进行下一个路径选择
marked[i] = false; // 状态重置
path.RemoveAt(path.Count - 1);
}
}