前端小白的数据结构学习总结——图
什么是图
图是一种非线性的数据结构,是对网的一种抽象的理解,比如说中国铁路网:

图片中可以看到,每个城市之间的由铁路连成了网,这个网中城市则为“点”,铁路则为“线”,那么我们这个“网”再抽象一点,就成了这样的一个图:
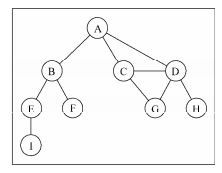
通常我们用G=(V, E)来表示图
一些概念
- vertex:上图中的圆表示一个城市,在图的概念中我们称其为“vertex(顶点)”
- edge:与顶点相连的表示的是城市之间的铁路,在图的概念中我们称其为“Edge(边)”
- weight(权):北京到上海铁路1400多公里,那么这个1400就是这边的weight(权),通常这种带有权的图,我们把他称之为网,比如中国铁路网,就是一个带权的图
- degree(度):一座城市链接的铁路的数目,也就是与顶点相连接的边的数目我们称其为“degree(度)”,在有向图中,因为边存在方向,所以度还分为入度(ID)和出度(OD)
无向图和有向图
上文中提到了Edge(边),这个边可以是具备方向的,那么有向图就很好理解了,边具备方向,像这样:
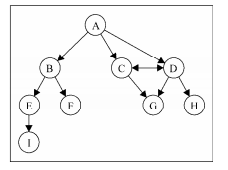
上图中顶点之间的边有用箭头来表示方向,这种边我们成为“弧(arc)”用<A, B>表示,而弧呢又分为弧头和弧尾,A -> B这样的一个弧中,我们将顶点A成为弧尾将顶点B成为弧头,通常用尖括号表示弧。
与之相反,无向图就是边没有方向的图,用小括号来表示一个边(A,B)
图的表示方式
我们可以用多种形式来标识一个图,有哪些顶点,以及顶点之间的链接关系
邻接矩阵
以矩阵的方式来描述一张图,横竖都是顶点,如果两顶点连接,那么这个位置的值为1,如果不连接则值为0
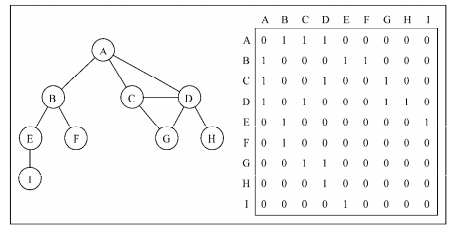
开发时,我们可以定义一个二维数组,那么这个数组应该是这样的
let array = [
// A B C D E F G H I
[0, 1, 1, 1, 0, 0, 0, 0, 0],// A
[1, 0, 0, 0, 1, 1, 0, 0, 0],// B
[1, 0, 0, 1, 0, 0, 1, 0, 0],// C
[1, 0, 1, 0, 0, 0, 1, 1, 0],// D
[0, 1, 0, 0, 0, 0, 0, 0, 1],// E
[0, 1, 0, 0, 0, 0, 0, 0, 0],// F
[0, 0, 1, 1, 0, 0, 0, 0, 0],// G
[0, 0, 0, 1, 0, 0, 0, 0, 0],// H
[0, 0, 0, 0, 1, 0, 0, 0, 0] // I
]
这里我们就用二维数组描述了一个图,但是上面我们有提到权的概念,如果是有权的图,那么这里二维数组中的值就应该是个权的值,但是这样一想,如果数值标识权的话,没有联通的顶点还弄用0表示吗?其实加权图的邻接矩阵中用无穷表示未连接,应该是这样:

邻接矩阵会存在一个问题,当这个图为稀疏图,即边相对于顶点很少的时候,可能会出现矩阵中大部分都是0,只有极少数为1,但是内存中还是会分配一个这么大的内存空间,这就造成了内存的浪费
邻接表
邻接表则是通过数组或者链表或者Map来描述一个图的链接关系
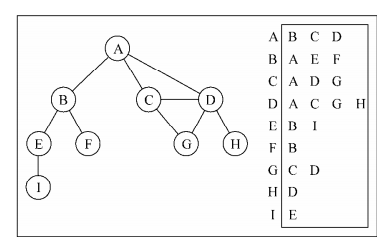
上图中用表来描述了一个图,以Map为例,key则为顶点,而value则为与顶点相连接的顶点集合,js中可能是这样的
let map = {
"A" : ["B", "C", "D"],
"B" : ["A", "E", "F"],
"C" : ["A", "D", "G"]
// ...
}
但是如果说边是带权的,那邻接表应该如何来描述呢?首先value这里如果是顶点的集合,那就是不行的,不能清楚的描述权,所以value应该是边的集合
let map = {
"A" : [
{
vertex : "B",
weight : 100
},
{
vertex : "C",
weight : 1
}
]
// ...
}
实现一个Graph类
首先构造函数中初始化一个map,用来存放顶点以及边的数据,我们以一个有向的无权图为例

class Graph{
constructor(){
this.vertexMap = new Map();
}
}
这个这个图可以添加顶点,将顶点传入,先判断是否重复传入,如果图中已经存在则不再添加
class Graph{
constructor(){
this.vertexMap = new Map();
}
addVertex(vertex){
// 先判断顶点是否已经添加,如果已经添加则不再添加
if(!this.vertexMap.has(vertex)){
this.vertexMap.set(vertex, []);
}
}
// 同时,定义一个获取所有顶点的方法
getVertexes(){
return this.vertexMap.keys();
}
}
添加完了顶点我们还能添加边,要描述边,那么自然需要两个顶点来描述,所以这个方法传入两个参数,第一个参数为弧尾,第二个参数为弧头
class Graph{
constructor(){
this.vertexMap = new Map();
}
addEdge(vertex1, vertex2){
// 先判断弧头是否经存在,不存在的话先保存弧头
if(!this.vertexMap.has(vertex1)){
this.vertexMap.set(vertex1, [vertex2]);
}else{
this.vertexMap.get(vertex1).push(vertex2);
}
}
}
基本的方法实现完了,实现一个打印方法看一看
class Graph{
constructor(){
this.vertexMap = new Map();
}
print(){
for(let item of this.vertexMap){
console.log(item[0] + "-->", item[1]);
}
}
}
let g = new Graph();
let vertex = ["A", "B", "C", "D", "E", "F", "G", "H", "I"];
g.addEdge("A", "B");
g.addEdge("A", "C");
g.addEdge("A", "D");
g.addEdge("B", "E");
g.addEdge("B", "F");
g.addEdge("C", "D");
g.addEdge("C", "G");
g.addEdge("D", "G");
g.addEdge("D", "H");
g.print();
最终执行以下能看到结果
A--> [ 'B', 'C', 'D' ]
B--> [ 'E', 'F' ]
C--> [ 'D', 'G' ]
D--> [ 'C', 'G', 'H' ]
E--> [ 'I' ]
图的遍历
我们图中任意一个顶点都可以作为遍历的起点,遍历的就意味着要确保每一个顶点都被访问到,其实遍历的思路非常简单,首先获取到起始点,然后根据起始点的边找到其连接的顶点,然后这样一直循环下去,但是这里就会出现两种情况深度优先遍历和广度优先遍历
广度优先搜索
BFS(Breadth Frist Search),顾名思义先大范围搜索,比如说对于这个图

假如我们以顶点A为起点,那么广度优先搜索的顺序就应该是A-B-C-D-E-.....
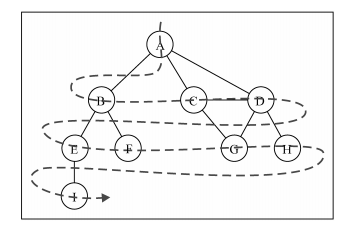
那么我们的遍历逻辑应该是
- 选取一点为起始点
- 找到该点的邻接点
- 遍历邻接点找到各自的邻接点
- 一直循环知道所有的点都访问到
深度优先搜索
DFS(Depth First Search),很好理解,先顺着一条路径一直访问顶点,还是一这个图为例

那么顶点的访问顺序应该是A-B-E-I-F-C-G-D-H
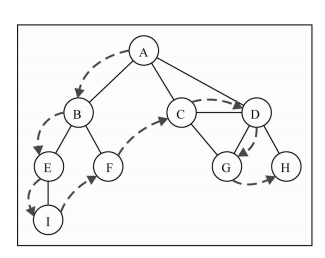
那么我们的逻辑应该是(有点混乱,后面会详细说)
- 选取起始点
- 获得起始点的第一个邻接点
- 循环上个步骤直到这条路径走完访问到最后一个顶点
- 向上返回到分支的地方访问另一个邻接点
- 继续走完这个路径
两种算法的相同点和不同点
其实对于顶点来说,无非就是三种状态
- 没找到
- 找到了
- 找到了并且获取了所有的邻接点
那么我们在遍历的过程中,需要针对顶点不同的状态做不同的逻辑处理,比如
- 遍历的时候发现这个顶点之前已经获取了所有的邻接点,那么就不会再访问了
- 上面介绍深度优先搜索的时候中,遍历逻辑步骤4,当我们一条路径走完后,需要往回走找到分支点,那么这个分支点是什么呢?这便是已经找到的但是没有获取邻接点的顶点
其实无论是深度优先还是广度优先,上述的思路都是一致的,但是不同点在哪呢,主要是就在于上文中提到的容器,我们这里放入容器的顺序是
- 找到顶点
- 按顺序将顶点放入容器
- 按顺序取出顶点
- 获取取出的顶点的邻接点
- 再循环到步骤2
上文提到了按顺序,放进容器按顺序,从容器中拿出按顺序,而这两个算法的不同点就在于顺序不同。
- 深度优先搜索:将数据储存在栈(先入后出)中
- 广度优先搜索:将数据存储在队列(先入先出)中
还是以这个图为例,我们用数组模拟栈和队列:

深度优先搜索,以顶点A为起始点举例
// 定义一个栈,入栈从数组尾部添加,出栈从数组尾部取值
let stack = []
// 首先找到起始点A的邻接点, 并且入栈,A标记为不再访问
stack = [D, C, B]
// 从尾部出栈,把B取出来,获取B的邻接点, B被标记为不再访问
stack = [D, C]
B - E , B - F
// E, F入栈
stack = [D, C, F, E]
// E出栈获取邻接点
stack = [D, C, F]
E - I
// I 入栈
stack = [D, C, F, I]
// I从出栈获取邻接点
stack = [D, C, F]
I - E
// F出栈
// .......
广度优先搜索,同样以顶点A为起始点举例
// 定义一个队列, 添加从数组尾部添加,取出从数组首部取值
let queue = []
// 首先找到起始点A的邻接点,并且加入队列,A标记为不再访问
queue = [B, C, D]
// 从队列首部取出顶点B,获取顶点B的邻接点,B被标记为不再访问
queue = [C, D]
B - E, B - F
// E, F入队列
queue = [C, D, E, F]
// 从首部取出顶点C,获取领接点,C被标记为不再访问
queue = [D, E, F]
C - G, C - D
// D已经存在于队列中,所以只有G入队列
queue = [D, E, F, G]
// 从队列中取出顶点D.....
深度优先搜索代码实现
前面的例子中,我们提到了用代码实现了一个Graph类,并且添加了一些顶点和边,最终打印了结果,接下来,我们接着这个例子,用代码实现一个深度优先搜索,这里就直接贴了,代码注释中有讲解
// 首先定义一个DFS函数,因为是要对图进行深度优先搜索,所以参数接收一个Graph的实例
let DFS = function(graph){
// 接收到实例后,首先获取图中的顶点
let vertexes = graph.getVertexes();
// 定义一个set保存不用再访问的顶点
let notVisitAgainVertexes = new Set();
// 定义一个访问节点的方法
let visit = function(vertex){
// 先判断当前顶点是不是不用再次访问,是的话这次执行直接跳出
if(notVisitAgainVertexes.has(vertex)){
return;
}
// 将该顶点添加到“不再访问”的容器中
notVisitAgainVertexes.add(vertex);
// 获取该顶点的邻接点
let neighborVertexes = graph.vertexMap.get(vertex);
// 如果存在邻接点,则递归调用visit
if(neighborVertexes instanceof Array){
for(let i = 0; i < neighborVertexes.length; i++){
visit(neighborVertexes[i]);
}
}
}
// 遍历所有顶点,并且执行visit
for(let vertex of vertexes){
visit(vertex);
}
}
上面代码中,我们通过递归调用了visit函数实现了深度优先遍历,我们在visit函数中加一个console.log可以看到结果
按顺序访问顶点 A
按顺序访问顶点 B
按顺序访问顶点 E
按顺序访问顶点 I
按顺序访问顶点 F
按顺序访问顶点 C
按顺序访问顶点 D
按顺序访问顶点 G
按顺序访问顶点 H
是不是和这个图一致

广度优先搜索代码实现
未完待续





