hdoj 4828 卡特兰数取模

Grids

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 93    Accepted Submission(s): 25

Problem Description

　　度度熊近期非常喜欢玩游戏。这一天他在纸上画了一个2行N列的长方形格子。

他想把1到2N这些数依次放进去。可是为了使格子看起来优美，他想找到使每行每列都递增的方案。只是画了非常久，他发现方案数实在是太多了。度度熊想知道，有多少种放数字的方法能满足上面的条件？

 

Input

　　第一行为数据组数T(1<=T<=100000)。
　　然后T行，每行为一个数N(1<=N<=1000000)表示长方形的大小。

 

Output

　　对于每组数据，输出符合题意的方案数。因为数字可能很大，你仅仅须要把最后的结果对1000000007取模就可以。

 

Sample Input

2
1
3

 

Sample Output

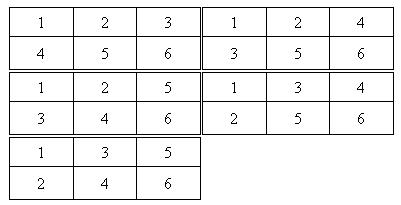
Case #1:
1
Case #2:
5
Hint
对于第二组例子。共5种方案。详细方案为：
 
 

 

Source

2014年百度之星程序设计大赛 - 初赛（第一轮）

通过打表得出前7项分别为1,2,5,14,42,132,429，可知答案为卡特兰数h(n)=C(2n,n)/(n+1)=h(n-1)*(4*n-2)/(n+1)。

一開始採用组合数分解素因子+二分求幂求组合数取模，但是会TLE，组合数求模相关知识http://hi.baidu.com/aekdycoin/item/e051d6616ce60294c5d249d7。渣代码例如以下：

#include <stdio.h>
#include <string>
#include <iostream>
#include<vector>
#include<cmath>
#include<algorithm>
using namespace std;
const int N = 2000005;
const int n=148955;
bool a[N];//a[]的长度比pr[]的长度长得多
int pr[n];
#define MOD 1000000007
int num;
void Prime2()
{
    memset(a, 0, N*sizeof(a[0]));
    int i, j;
	num = 0;
    a[0]=a[1]=1;
    for(i = 2; i < N; ++i)
	{
        if(!(a[i])) pr[num++] = i;
        for(j = 0; (j<num && i*pr[j]<N); ++j)
		{
            a[i*pr[j]] = 1;
            if(!(i%pr[j])) break;
        }
    }
}
int val[n],len;
void calcJC(int n,int id,int flag){
	int ans=0,y,p=pr[id];
	while(n){
		y=n/p;
		ans+=y;
		n=y;
	}
	val[id]=val[id]+ans*flag;
}
__int64 extgcd(__int64 a,__int64 b,__int64 &x,__int64 &y)
{
    if(b==0)
    {
        x=1,y=0;
        return a;
    }
    __int64 r=extgcd(b,a%b,x,y);
    __int64 t=x;x=y;y=t-a/b*y;
    return r;
}
int MPow(int p,int e){
	if(e==0)return 1;
	else if(e==1)return p;
	int t=p,ans=1;
	while(e){
		if(e&1)ans=(ans*t)%MOD;
		t=(t*t)%MOD;
		e>>=1;
	}
	return ans;
}
int main()
{
	Prime2();
	int txt,l=1,k,i;
	__int64 ans,x,y;
	scanf("%d",&txt);
	while(txt--){
		scanf("%d",&k);
		memset(val,0,sizeof(val));
	 	for(i=0;pr[i]<=2*k;++i)
			calcJC(2*k,i,1);
		for(i=0;pr[i]<=k;++i)
			calcJC(k,i,-2);
		ans=1;
		for(i=0;pr[i]<=2*k;++i){
		//	if(val[i]>0)printf("%d^%d ",pr[i],val[i]);
			ans=(ans*MPow(pr[i],val[i]))%MOD;
		}
		extgcd(k+1,MOD,x,y);
		x=(x+MOD)%MOD;
		ans=(ans*x)%MOD;
		printf("%I64d\n",ans);
	}
	return 0;
}

无奈，看到n范围不是非常大，直接打表吧、、、

#include <stdio.h>
#include <string>
#include <iostream>
#include<vector>
#include<cmath>
#include<algorithm>
using namespace std;
#define MOD 1000000007
const int N = 1000001;
int a[N];
__int64 extgcd(__int64 a,__int64 b,__int64 &x,__int64 &y)
{
    if(b==0)
    {
        x=1,y=0;
        return a;
    }
    __int64 r=extgcd(b,a%b,x,y);
    __int64 t=x;x=y;y=t-a/b*y;
    return r;
}
void calcCATALAN(int n){
	__int64 x,y;
	a[1]=1;
	int i;
	for(i=2;i<n;++i){
		x=a[i-1];
		a[i]=(x*(4*i-2))%MOD;
		extgcd(i+1,MOD,x,y);
		x=(x+MOD)%MOD;
		a[i]=(a[i]*x)%MOD;
	}
}
int main()
{
	calcCATALAN(N);
	int txt,l=1,k;
	scanf("%d",&txt);
	while(txt--){
		scanf("%d",&k);
		printf("Case #%d:\n",l++);
		printf("%d\n",a[k]);
	}
	return 0;
}