支持向量机(SVM)（二）-- 拉格朗日对偶（Lagrange duality）

简单介绍：

1、在之前我们把要寻找最优的切割超平面的问题转化为带有一系列不等式约束的优化问题。这个最优化问题被称作原问题。

我们不会直接解它，而是把它转化为对偶问题进行解决。

2、为了使问题变得易于处理。我们的方法是把目标函数和约束所有融入一个新的函数，为了使问题变得易于处理，我们的方法是把目标函数和约束所有融入一个新的函数，即拉格朗日函数，再通过这个函数来寻找最长处。即拉格朗日函数，再通过这个函数来寻找最长处。

3、约束条件能够分成不等式约束条件和等式约束条件，仅仅有等式约束条件的问题我们在高等数学课程中已经学习过了，其解决方法是直接将等式约束增加原问题构造出拉格朗日函数，然后求导就可以。如今考虑更加一般性的问题：带不等式约束和等式约束的极值问题怎样构造拉格朗日函数求解。

学习拉格朗日对偶原理重要的是理解构造所得的原始问题和原函数的等价性。以及原始问题和对偶问题解得等价性。

回顾一下之前得到的目标函数

要求解这个式子。我们能够通过求解对偶问题得到最优解。这就是线性可分条件下支持向量机的对偶算法，这样做的长处在于：一者对偶问题往往更easy求解；二者能够自然的引入核函数，进而推广到非线性分类问题。

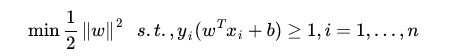
1、我们下看以下的一个式子

上面是要求解的目标函数及其条件。

我们能够得到拉格朗日公式为

在这里被称为拉格朗日算子。

然后分别对w和求偏导，使得偏导数等于0，然后解出和；

以下我们将要产生一个既有等式又有不等式条件限制的式子。我们能够叫做原始优化问题，这里简介下拉格朗日对偶的原理。例如以下式子：

上述式子有两个条件（等式条件和不等式条件）

由此我们定义一般化的拉格朗日公式

这里的和都是拉格朗日算子。不要忘了我们求解的是最小值。

设例如以下等式：

这里的P代表primal。

我们设例如以下约束条件（primal constraints）：

假设条件不所有满足的话。我们总能够调整和使最大值出现正无穷，即会出现以下情况：

因此我们能够得出例如以下式子：

这样我们原来要求的min f(w)能够转换成求了。

同一时候我们设

将问题转化为先求拉格朗日关于的最小值，这个时候就把和看做常量。之后再求最大值。

例如以下：

这个问题就是原问题的对偶问题。相对于原问题仅仅是更换了min和max的顺序。而一般更换顺序的结果是Max Min(X) <= Min Max(X)。

然而在这里两者相等。由此我们能够设例如以下：

所以在一定的条件下我们能够得到：

因此我们能够解决原问题的对偶问题，可是我们还要看看条件是什么。

如果f和g都是凸函数，h是仿射的(仿射的含义：存在ai, bi，使得)。而且还要满足存在w使得全部的i都有。

有了以上的如果，那么一定会存在使得是原问题的解。是对偶问题的解。同一时候也满足

另外，还满足Karush-Kuhn-Tucker（ KKT condition）。例如以下式子：

所以假设满足了KKT条件，那么他们就是原问题和对偶问题的解。

我们从式子和式子能够看出假设那么。

这个也就说明时。w处于可行域的边界上。这时才是起作用的约束。

而其它位于可行域内部的（）点都是不起作用的约束，当中也就是的时候。这个KKT双重补足条件会用来解释支持向量和SMO的收敛測试。