混合高斯模型分类
import numpy as np import math import csv import matplotlib.pyplot as plt class Model(object): def __init__(self,filename,alpha,iter_num,num_samples,k,sigma,u): self.filename = filename self.alpha = alpha self.iter_num = iter_num self.num_samples = num_samples self.k = k self.sigma = sigma self.u = u self.prob = np.zeros((self.num_samples,self.k)) def LoadCsv(self): lines = csv.reader(open(self.filename, 'r')) data = list(lines) for i in range(1, len(data)): data[i] = [float(x) for x in data[i]] result = np.array(data[1:]) self.data = result[:,1:] self.data = np.matrix(self.data) def E_Step(self): #prob = np.zeros((self.num_samples,self.k)) for i in range(self.num_samples): sum_p = 0 for j in range(self.k): sum_p+= self.alpha[j]*math.exp(-0.5*(self.data[i,:]-self.u[j,:]) *self.sigma[j].I*np.transpose(self.data[i,:]-self.u[j,:]))/(np.sqrt(np.linalg.det(self.sigma[j])) *2*math.pi) for j in range(self.k): number = math.exp(-0.5*(self.data[i,:]-self.u[j,:]) *self.sigma[j].I*np.transpose(self.data[i,:]-self.u[j,:]))/(np.sqrt(np.linalg.det(self.sigma[j])) *2*math.pi) self.prob[i,j]=self.alpha[j]*number/sum_p #return prob def M_Step(self): self.E_Step() for i in range(self.k): denom =0 numer = 0 sigma_denom = 0 for j in range(self.num_samples): denom += self.prob[j,i]*self.data[j,:] numer += self.prob[j,i] self.u[i,:] = denom/numer self.alpha[i] = numer/self.num_samples for j in range(self.num_samples): sigma_denom += self.prob[j,i]*np.transpose(self.data[j,:]-self.u[i,:])*(self.data[j,:]-self.u[i,:]) self.sigma[i] = sigma_denom/numer def Update(self): self.LoadCsv() for i in range(self.iter_num): print('------%d'%i) self.M_Step() cluster=np.zeros(self.num_samples) #划分成簇 for i in range(self.num_samples): for j in range(self.k): if self.prob[i,j] == max(self.prob[i,:]): cluster[i] = j return cluster def Show(self): cluster = self.Update() plt.figure() color=['red','green','blue'] for i in range(self.num_samples): #print(self.data[i,0]) plt.scatter(self.data[i, 0], self.data[i,1], c=color[int(cluster[i])], s=25, alpha=0.4, marker='o') plt.xlabel('density') plt.ylabel('sugar content') plt.savefig('高斯混合聚类模型-50代.jpg') plt.show() filename = 'D:\DeepLearning(7.8-)\data\watermelon4_0.csv' alpha = [0.33,0.33,0.34] u = np.array([[0.403,0.237],[0.714,0.346],[0.532,0.472]]) u = np.matrix(u) k =3 num_samples = 30 iter_num = 50 sigma =[] sigma.append(np.matrix([[0.1,0.0],[0.0,0.1]])) sigma.append(np.matrix([[0.1,0.0],[0.0,0.1]])) sigma.append(np.matrix([[0.1,0.0],[0.0,0.1]])) m = Model(filename,alpha,iter_num,num_samples,k,sigma,u) m.Show() #cluster =m.Update() #print(cluster)
结果:
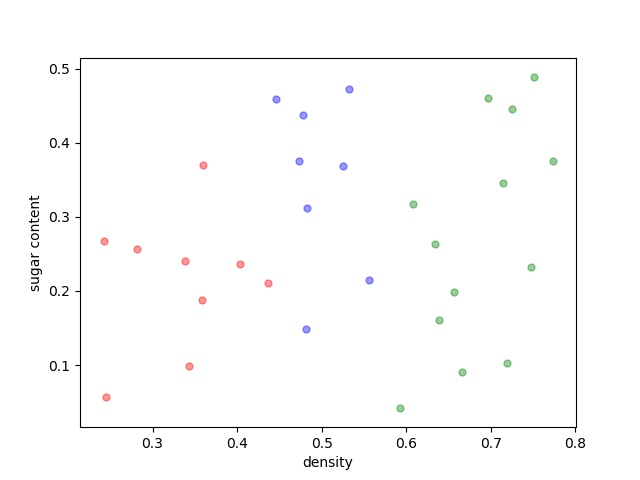
西瓜书上的 西瓜数据集 :https://files.cnblogs.com/files/jzcbest1016/data.rar
高斯混合聚类模型伪代码:
输入:样本集D ={x1,x2,....xm}
高斯混合成分个数k
过程:
初始化高斯混合分布的模型参数{(ai,ui,∑i)} 三个参数含义:分别为混合系数,均值向量,协方差矩阵
迭代:
for j = 1,2,......,m do
根据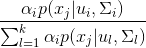 计算xj的各混合成分生成的后验概率
计算xj的各混合成分生成的后验概率
 pm等于上面那个式子
pm等于上面那个式子
end for
for i =1,2,....k do
计算新均值向量 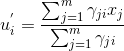
计算新协方差矩阵 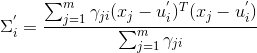
计算新混合系数 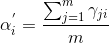
end for
将模型参数{(ai,ui,∑i)|1<=i<=k}更新为{(ai’,ui’,∑i’)|1<=i<=k}
until 满足停止条件
Ci = Ø (1<=i<=k)
for j =1,2,...m do
根据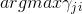 (i=1,2,....k) 确定xj的簇标记λj (确定属于哪个i)
(i=1,2,....k) 确定xj的簇标记λj (确定属于哪个i)
将xj划分相应的簇:
end for
输出:簇划分c = {c1,c2.....ck}


