矩阵相乘优化(Gemm)
一、参考链接
http://tvm.d2l.ai/
https://www.cs.utexas.edu/users/pingali/CS378/2008sp/papers/gotoPaper.pdf
https://zhuanlan.zhihu.com/p/65436463
https://github.com/flame/how-to-optimize-gemm/
二、矩阵相乘优化方法
假设矩阵C = 矩阵A * 矩阵B; 矩阵A的shape为(M, K),矩阵B的shape为(K, N),矩阵C的shape为(m,n)。
普通的矩阵为 A的一行乘以B的一列,如下图:
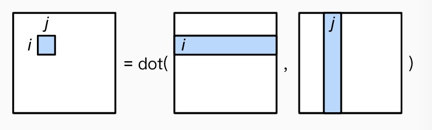
c/c++/python基本上是以行存储优先的,本文将以行存储优先作为基础进行优化分析。
考虑两种情况:
(1)当AB矩阵较小时,根据计算机结构可知,当从RAM中读取AB矩阵内存,根据局部性原理可以将AB矩阵放到cache中,因为cpu访问cache比访问主存的快。
(2)当AB矩阵较大时,超过cache大小时,根据矩阵乘的普通方法,由于访问“行优先存储的B矩阵”的时候内存不连续(读取B矩阵的一列),造成缓存cache频繁的换入换出,从RAM读取内存的次数大于AB矩阵的大小。因此第一种优化方法:
1. 向量化(SIMD)
向量化可以使一条指令并行的使多个相同操作数执行相同的操作,减少每次循环迭代时评估操作类型的开销。
2. 内存对齐
内存对齐的原则:任何K字节的基本对象的地址必须都是K的倍数。
“假设 cache line 为 32B。待访问数据大小为 64B,地址在 0x80000001,则需要占用 3 条 cache 映射表项;若地址在 0x80000000 则只需要 2 条。内存对齐变相地提高了 cache 命中率。” 假定kernel一次计算执行4*4 大小的block, 根据MMult_4x4_7.c 和 MMult_4x4_8.c 代码,可以看出MMult_4x4_8.c使用了偏移量完成内存对齐。
3. 分块

图中共有6中拆分方法,依次分析:
(1) 拆分K,A矩阵拆成多列,B矩阵拆成多行。拆分M,A的一列拆分成三个block。拆分N,B的一行也可以拆分成多个小slice,每个slice放到寄存器中。遍历A的列,A的每个block乘以B的一行,得到矩阵C的一行的部分值。 拆分之后Aip为(mc, kc), Bpj为(kc, nr), Cij为(mc, nr)。
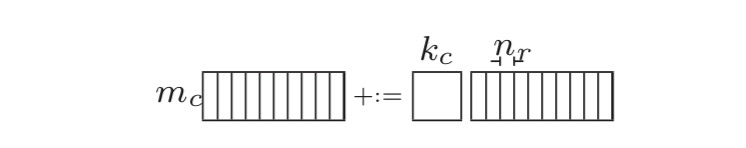
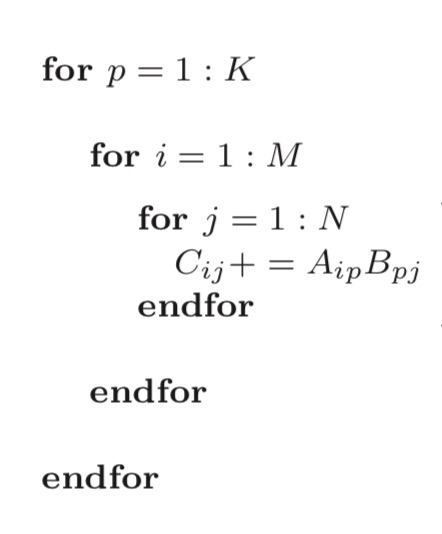

如果kc*mc很小,那么Aip、Bpj、Cij都放入cache中,Aip(A矩阵的一个block)只需要被加载进cache一次,提高了cache命中率。对Ai和Bj进行pack使其内存连续。由于处理B矩阵是按照每个slice依次进行,所以这种划分更适合于列存储优先的矩阵乘。
(2) 拆分K,A拆分成多列,B拆成多行。拆分N,B的一行被拆分为三个block。拆分M,A的一列被拆分为多个slice。A的一列乘以B的每个block,得到矩阵C的一列的部分值。


类似于(1), 只是变成A的一行乘以B的一个block。所以这种划分更适合于行存储优先的矩阵乘。
(3) 拆分N,B矩阵被拆分为多列。再拆分K,A拆分成多列,B拆成多个block。拆分M,A的一列被拆分为多个小block。A的一列乘以B的每个block,得到矩阵C的一列的部分值。

这种划分与(2)的划分唯一的区别是,访问B矩阵是按列还是按行。很显然(2)的划分方式好于(3)。
(4) 类似于普通矩阵乘,A的一行*B的一列。然后在K拆分,将A矩阵的每行划分为多个block, 将B矩阵的每列划分为多个block。

每次执行可以得到C矩阵一个block的值。当MNK非常大时,cache无法存下Cj,所以划分方法没有什么优势。
(5) 类似于(4), 都是每次执行可以得到C矩阵的一个block的值。同样当MNK非常大时,cache无妨存下Cj,所以该画风方法没有什么优势。

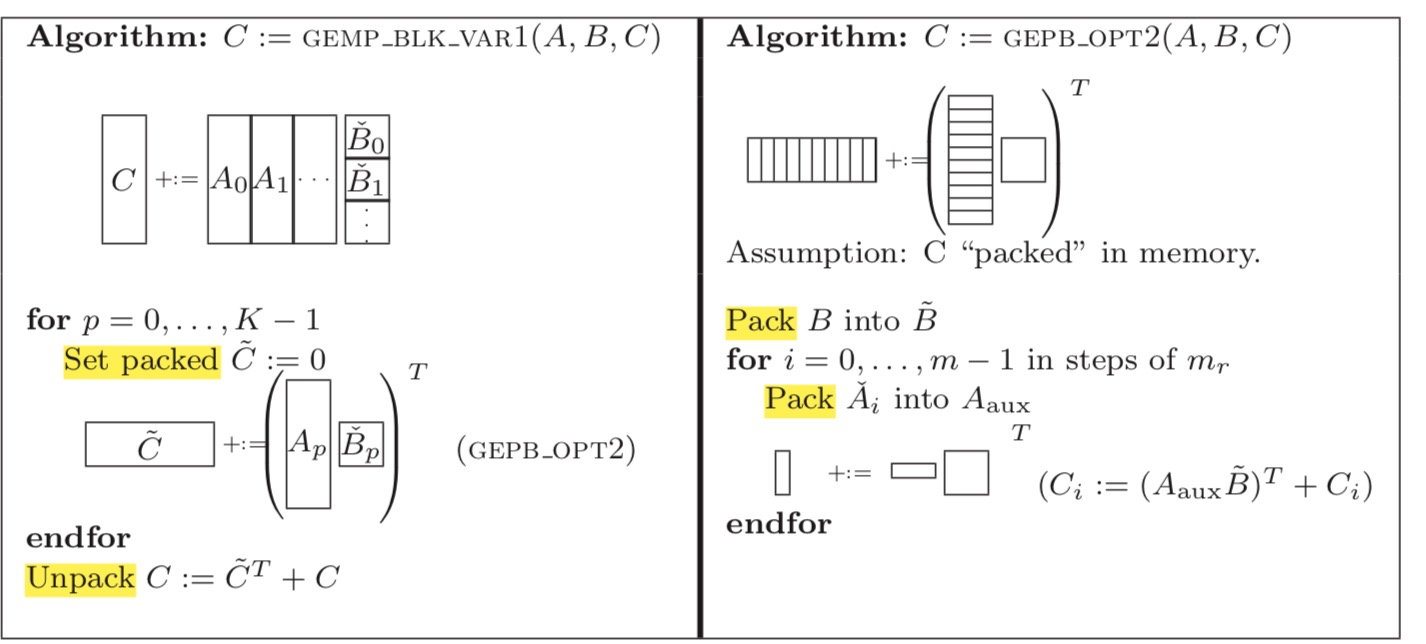
(6) 类似于(1)。不一样在于:对A矩阵的block遍历是按行访问。

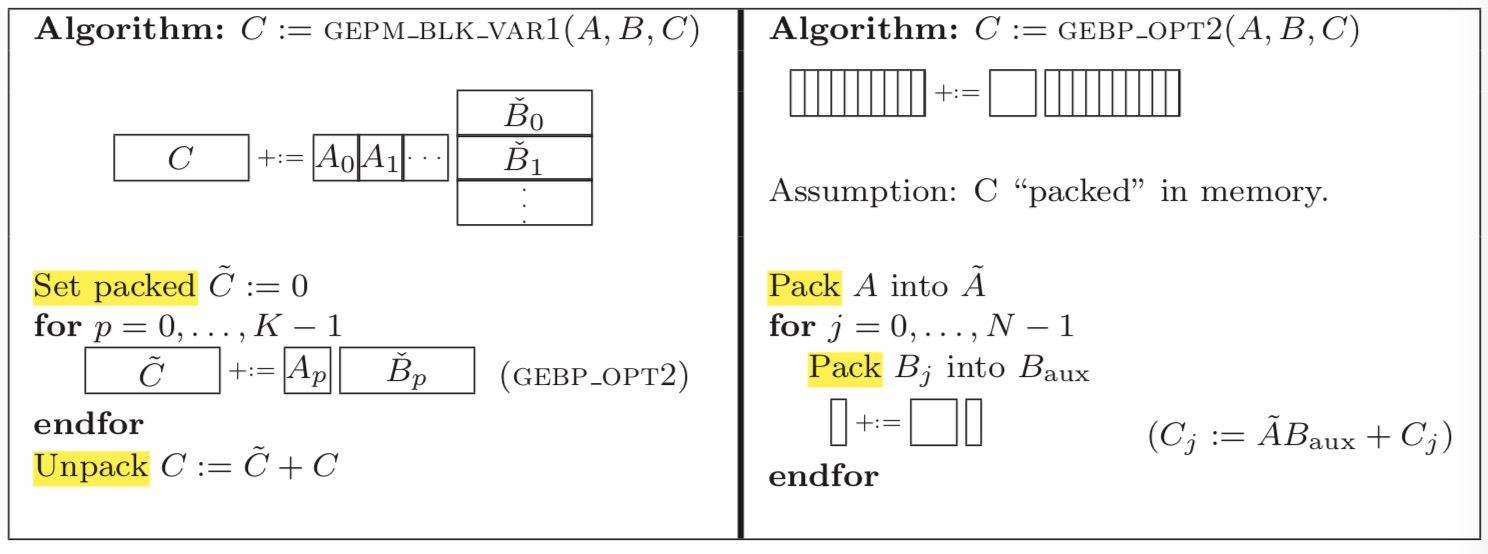
和(1)相比,最外层循环是i,而非p。遍历顺序为A0*B0 + A1*B1 + .... + Ap*Bp 才能得到C一行的最终值,因此需要不断的更新C这一行的值,可以使用一个顺序的cache数组存放 pack ![]() ,最后在unpack的时候累加。这与(1)中的按列访问A矩阵的block不同,(1)中Ci += Ai*
,最后在unpack的时候累加。这与(1)中的按列访问A矩阵的block不同,(1)中Ci += Ai*![]() , 在最内层循环时只需要使用寄存器存储每次Ai*Bpj的结果。
, 在最内层循环时只需要使用寄存器存储每次Ai*Bpj的结果。
由于在循环外 cache 级别 unpack C 远复杂于在循环内 register 级别 unpack C,因此(1)比(6)好。


