gmoj 3976. 【NOI2015模拟1.17】⑨

\(Problem\)

给你\(n\)个点，以及\(m\)个有贡献的点。
而后给你一个简单多边形（由那\(n\)个点组成），求里面的有贡献的点的贡献和。

这是样例↓

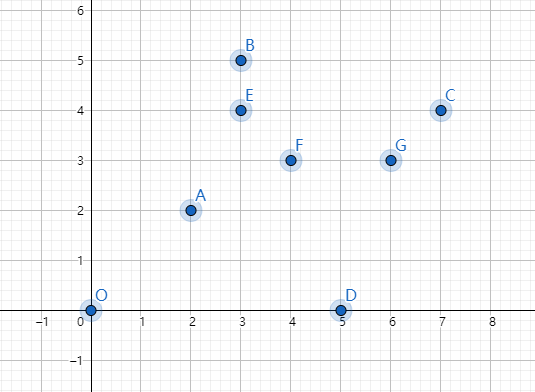
\(Solution\)

显然我们可以将这个简单多边形拆成一些与原点相连的三角形。

也就是说，对于\(AEF\)，可以变成\(HEF-HAE-HAF\)，而对于正负的取值：
若边是按照逆时针来看的，则向右走的边为负，向左走的边为正。也就是说起点极角大于终点的话为负，否则为正。
如此我们可以预处理出所以两个点与原点组成的三角形内的贡献和，然后按上述操作即可。

对于预处理有比较多的方法可以实施。

\(Method 1\)

暴力容斥即可。

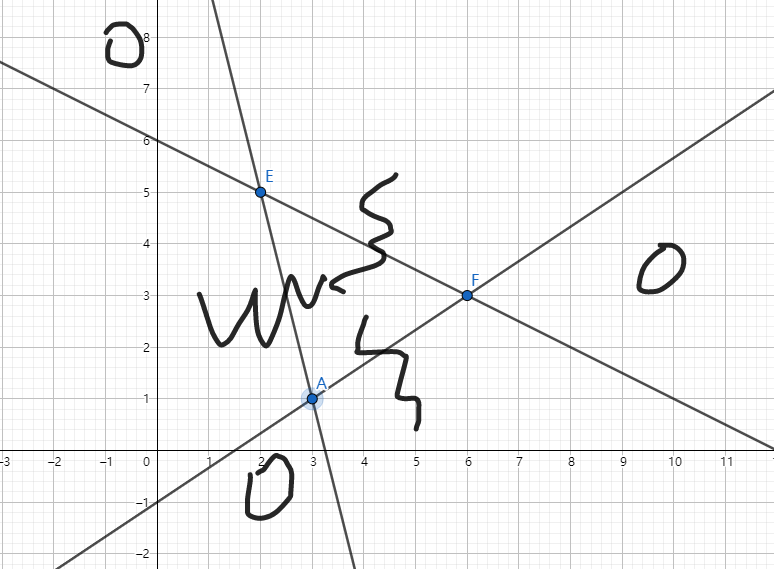
我们可以算出一个点射出两条线的夹角范围内的贡献，如此就可以进行上述操作了。

\(Method 2\)

对于一个贡献点是否产生贡献，我们可以看它上面有多少条多边形的线段，如果为奇数，则产生了贡献。
这样，我们可以对于一个多边形上的点，对剩下的点进行极角排序，而后扫一遍，并且用数据结构维护即可。

\(Method 3\)

这个不会，要问问\(xiaoqi\)。
现在会了（在\(xiaoqi\)大佬%%%的谆谆教导下）
我们对于每一个结点，都用极角排序得到青蛙的顺序。

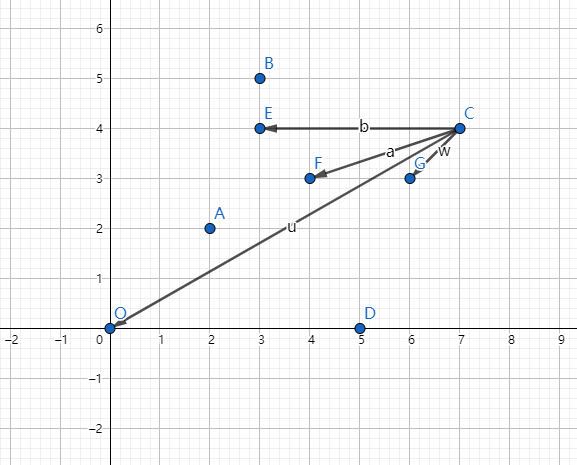
（其中\(A,B,C,D\)是结点，\(E,F,G\)是青蛙）
对于\(C\)这个节点，极角最小的是\(G\)，其次是\(E\)，接着是\(F\)。
也就是说，极角是以\(CO\)为\(x\)轴建立出来的坐标轴的极角
对于两个点与原点组成的三角形的贡献，则可以这样表示：

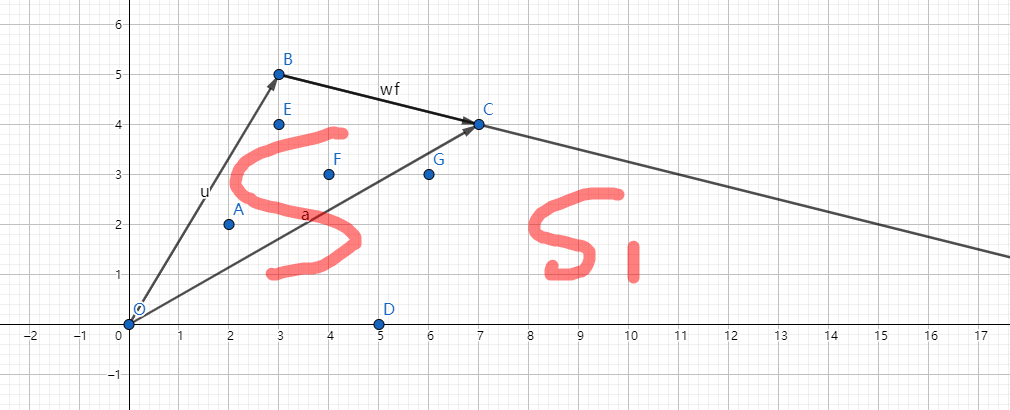
我们已知两个点，显然可以算出那些角度来（通过余弦定理）
\(S\)的贡献显然可以通过二分来得到。而\(S2\)的贡献也可以得到，于是就可以用\(O(n^2*logn)\)的时间得到结果了。

\(Code\)

#include <cstdio>
#include <algorithm>
#include <cmath>
#define N 1010
#define db double
#define ll long long
#define fo(x, a, b) for (int x = (a); x <= (b); x++)
#define fd(x, a, b) for (int x = (a); x >= (b); x--)
#define go(x) for (int p = tail[x], v; p; p = e[p].fr)
using namespace std;
const db pi = acos(-1);
struct node{int x, y, val; db sp;}fg[N];
struct nd{int x, y, fr; db sp;}a[N];
int n, m, Q, f[N][N], qz[N][N];
db sp[N][N];

inline int read() {
	int x = 0, f = 0; char c = getchar();
	while (c < '0' || c > '9') f = (c == '-') ? 1 : f, c = getchar();
	while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
	return f ? -x : x;
}

inline bool cmp1(nd x, nd y) {return x.sp > y.sp;}

inline bool cmp(node x, node y) {return x.sp < y.sp;}

inline bool rec(nd x, nd y) {return x.fr < y.fr;}

int erfen(int x, int l, int r, db val) {
	int mid, can_ = 0;
	while (l <= r) {
		mid = (l + r) >> 1;
		if (sp[x][mid] > val) r = mid - 1;
		else can_ = mid, l = mid + 1;
	}
	return qz[x][can_];
}

db sqr(db x) {return x * x;}

void prepare() {
	sort(a + 1, a + n + 1, cmp1);
	fo(i, 1, n) {
		fo(j, 1, m) {
			fg[j].sp = atan2(fg[j].y - a[i].y, fg[j].x - a[i].x);
			if (fg[j].sp < 0) fg[j].sp += 2 * pi;
			if (fg[j].sp < pi + a[i].sp) fg[j].sp += pi - a[i].sp;
			else fg[j].sp -= pi + a[i].sp;
		}
		sort(fg + 1, fg + m + 1, cmp);
		fo(j, 1, m) qz[i][j] = qz[i][j - 1] + fg[j].val, sp[i][j] = fg[j].sp;
	}
	fo(i, 1, n) fo(j, i + 1, n) {
		db O_A = sqrt(sqr(a[i].x) + sqr(a[i].y));
		db O_B = sqrt(sqr(a[j].x) + sqr(a[j].y));
		db A_B = sqrt(sqr(a[i].x - a[j].x) + sqr(a[i].y - a[j].y));
		db angle1 = acos((sqr(O_A) + sqr(A_B) - sqr(O_B)) / (2.0 * O_A * A_B));
		db angle2 = pi - acos((sqr(A_B) + sqr(O_B) - sqr(O_A)) / (2 * A_B * O_B));
		int t1 = erfen(i, 1, m, angle1);
		int t2 = erfen(j, 1, m, angle2);
		f[a[i].fr][a[j].fr] = f[a[j].fr][a[i].fr] = t1 - t2;
	}
	sort(a + 1, a + n + 1, rec); 
}

int main()
{
	n = read(), m = read();
	fo(i, 1, n) {
		a[i].x = read() + 10001, a[i].y = read() + 10001;
		a[i].fr = i, a[i].sp = atan2(a[i].y, a[i].x);
	}
	fo(i, 1, m) fg[i].x = read() + 10001, fg[i].y = read() + 10001, fg[i].val = read();
	prepare();
//	fo(i, 1, n) fo(j, 1, n)
//		printf("%d %d: %d\n", i, j, f[i][j]);
	Q = read();
	while (Q--) {
		int len = read(), fir = read();
		int now = fir, nex_, ans = 0;
		db val1 = atan2(a[now].y, a[now].x), val2;
//		if (val1 < 0) val1 += 2 * pi;
		fo(i, 2, len) {
			nex_ = read();
			val2 = atan2(a[nex_].y, a[nex_].x);
//			if (val2 < 0) val2 += 2 * pi;
			if (val2 > val1) ans += f[now][nex_];
			else ans -= f[now][nex_];
			now = nex_, val1 = val2;
		}
		val2 = atan2(a[fir].y, a[fir].x);
//		if (val2 < 0) val2 += 2 * pi;
		if (val2 > val1) ans += f[now][fir];
		else ans -= f[now][fir];
		printf("%d\n", ans < 0 ? -ans : ans);
	}
	return 0;
}