ARC109D - L
平面上一开始有三个点\((0,0),(0,1),(1,0)\)形成成L形(点连续),每次操作可以将一个点改变位置,使得得到的仍然是L形。给出终止L形的位置,问移动的最小步数。
\(|x|,|y|\le 10^9,T\le 10^3\)
有若干种阴间的分类讨论做法但是阳间的做法却不好想。
CF论坛中的一位大佬分享了个clean solution:
考虑\(L\)形重心的位置,考虑每次移动重心是怎样移动的,可以发现:重心能往8联通方向除了跨过顶点的方向外移动一格。
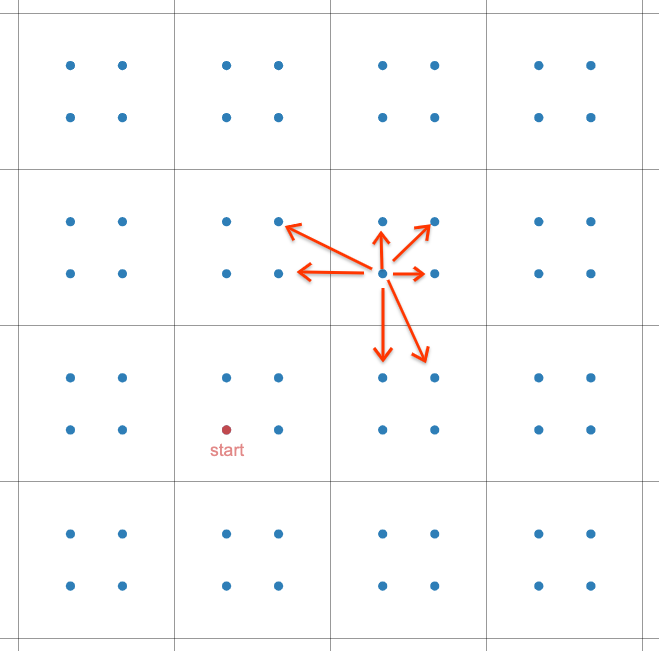
于是先把L形的坐标转化成重心的坐标,假如是8联通,那么答案为\(\max(|X|,|Y|)\)。加上走的过程中不能跨过顶点的限制,可以发现如果\(X\neq Y\)则仍然可以走过去,如果\(X=Y\)就需要偏离一下,然后后面也可以直接走过去,代价\(+1\)。
using namespace std;
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define x first
#define y second
pair<int,int> d[3];
ll X,Y;
void trans(){
sort(d,d+3);
if (d[0].x==d[1].x && d[0].y==d[2].y){
X=d[0].x*2;
Y=d[0].y*2;
}
else if (d[1].x==d[2].x && d[1].y==d[0].y){
X=d[1].x*2-1;
Y=d[1].y*2;
}
else if (d[1].x==d[0].x && d[1].y==d[2].y){
X=d[1].x*2;
Y=d[1].y*2-1;
}
else{//d[2].x==d[1].x && d[2].y==d[0].y
X=d[2].x*2-1;
Y=d[2].y*2-1;
}
}
int main(){
int T;
scanf("%d",&T);
while (T--){
for (int i=0;i<3;++i)
scanf("%lld%lld",&d[i].x,&d[i].y);
trans();
ll ans=max(abs(X),abs(Y));
if (X==Y && X!=0 && X!=1)
ans++;
printf("%lld\n",ans);
}
return 0;
}


