CF506E Mr. Kitayuta's Gift
CF506E
有个字符串,插入\(n\)个字符使得它变成回文串。
问形成的不同的回文串的个数。
(洛谷的题目大意有问题)
\(|s|\le 10^9\)
\(n\le 200\)
神仙题。
网上一堆博客讲得很清楚,那么这里就简单地复述一下。
先考虑暴力。设\(f_{i,l,r}\)表示回文串决定了前后\(i\)个字符,尽量给字符串匹配,剩下的字符串为\([l,r]\)的方案数。
\(g_i\)表示决定了前后\(i\)个字符,整个字符串匹配完了的方案数。
- \(l+1=r \and s_l=s_r \or l=r\)。转移至\(g_{i+1}\)
- \(s_l=s_r\)。转移至\(f_{i+1,l+1,r-1}\)和\(f_{i+1,l,r}\)。
- \(s_l\neq s_r\)。转移至\(f_{i+1,l+1,r}\)和\(f_{i+1,l,r-1}\)和\(f_{i+1,l,r}\)。
\(g_i\)转移至\(g_{i+1}\)。
系数自己补上。
可以发现这是个有限状态自动机上匹配的过程:
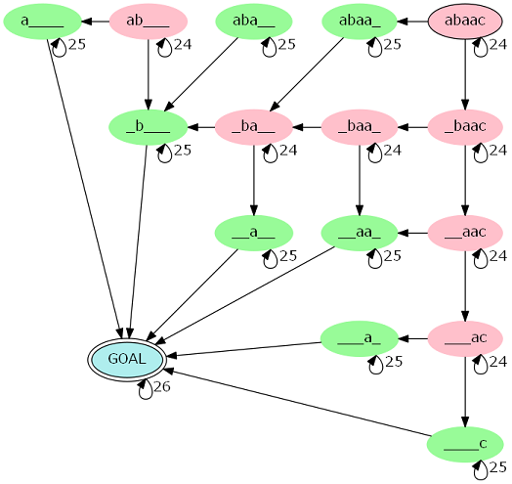
这里有\(O(|s|^2)\)个点,直接矩阵乘法会爆炸。
记\(s_l=s_r\)的点为绿点,\(s_l\ne s_r\)的点为红点。
从起点到终点有若干条路径,我们发现一条路径的贡献只跟经过的红点和绿点有关。
假如一条路径上有\(i\)个红点,那么就有\(\lceil\frac{len-i}{2}\rceil\)个绿点。
搞个类似于上面的dp来计算出每种路径出现了多少次。记作\(g_i\)。
把每个路径的贡献分别计算,时间复杂度\(O(|s|^4\lg n)\)。
还是过不去。把状态压成下面这样:
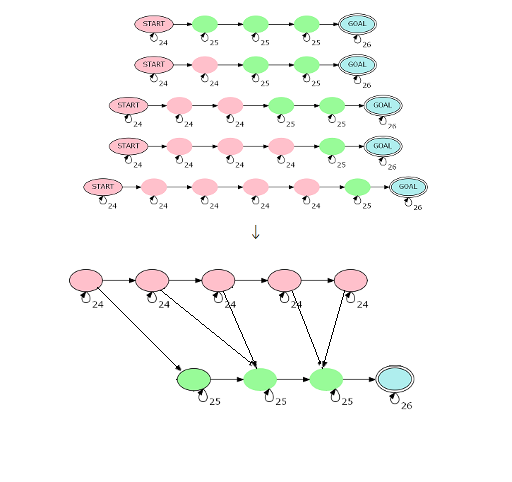
这样就只有\(\frac{3}{2}|s|\)个点。\(g_i\)挂在红点和绿点之间的横插边上。
直接矩阵乘法就好了。
如果是奇数的话这种方法还要修正一下:
在确定中间的那个数的时候,如果从\([i,i+1]\)转移过来,那就不合法。
那就再用个矩阵乘法把这个贡献减掉。具体建图和上面类似,\(g_i\)只算\([i,i+1]\)转移过来的贡献,终点没有自环。
有个常数优化的小trick:
由于矩阵乘法可以看做从小的编号向大的编号转移,于是如此枚举:j=i to n,k=i to j
using namespace std;
#include <cstdio>
#include <cstring>
#include <algorithm>
#define N 210
#define ll long long
#define mo 10007
int n,m;
char s[N];
int f[N][N][N],g[N];
void add(int &a,int b){a=(a+b)%mo;}
int tot;
struct Matrix{
int m[N*2][N*2];
} T,T0,S;
void multi(Matrix &a,Matrix &b){
static Matrix c;
for (int i=0;i<=tot;++i)
for (int j=i;j<=tot;++j){
ll sum=0;
for (int k=i;k<=j;++k)
sum+=a.m[i][k]*b.m[k][j];
c.m[i][j]=sum%mo;
}
memcpy(&a,&c,sizeof c);
}
void getpow(int n){
memset(&S,0,sizeof S);
for (int i=0;i<=tot;++i)
S.m[i][i]=1;
for (;n;n>>=1,multi(T,T))
if (n&1)
multi(S,T);
}
void build(bool er=1){
tot=n+((n-1)/2+1)+1-1;
memset(&T,0,sizeof T);
for (int i=0;i<n;++i){
if (i)
T.m[i][i]=24;
if (i<n-1)
T.m[i][i+1]=1;
int j=tot-((n-i-1)/2+1);
T.m[i][j]=g[i];
}
for (int i=n;i<tot;++i){
T.m[i][i]=25;
T.m[i][i+1]=1;
}
T.m[tot][tot]=(er?26:0);
}
int main(){
freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
scanf("%s%d",s+1,&m);
n=strlen(s+1);
f[1][n][0]=1;
for (int i=1;i<=n;++i)
for (int j=n;j>=i;--j)
for (int k=0;k<=n-(j-i+1);++k)
if (f[i][j][k]){
int v=f[i][j][k];
if (i+1==j && s[i]==s[j] || i==j)
add(g[k],v);
else if (s[i]==s[j])
add(f[i+1][j-1][k],v);
else{
add(f[i+1][j][k+1],v);
add(f[i][j-1][k+1],v);
}
}
build();
if (n+m&1){
getpow((n+m+1>>1)+1);
ll ans=S.m[0][tot];
for (int k=0;k<n;++k){
g[k]=0;
for (int i=1;i<n;++i)
if (s[i]==s[i+1])
add(g[k],f[i][i+1][k]);
}
build(0);
memset(&S,0,sizeof S);
getpow((n+m+1>>1)+1);
ans=(ans-S.m[0][tot]+mo)%mo;
printf("%d\n",ans);
}
else{
getpow((n+m>>1)+1);
printf("%d\n",S.m[0][tot]);
}
return 0;
}

