K-D tree

KD-tree是什么？
曾经的我以为那是一个神仙的数据结构，而后来就没有这么认为了。思想非常好懂，而且我第一次打出KD-tree时竟然没有怎么调试就过了某道题的样例。
不过，KD-tree尽量不要使用。虽然说它很好打，但是它的时间复杂度非常奇怪。如果你是大神，你可以自己推出来，而如果你是像我一样的蒟蒻，那么，你就当个水分神器来用吧。

---

K-D tree是什么？

K-D tree能干啥？

K-D tree是一个处理$k$维的几何问题的数据结构。
举个例子，K-D tree最简单的应用。给你一个平面，平面上有很多个点，每次询问一个矩形中有多少个点。
什么？这么水？直接扫描线AC之
好吧……我知道这东西能用扫描线来做，但这只是K-D tree的一个非常简单的应用罢了。

K-D tree长啥样？

放张图（来自wikipedia）

啊哈？这是个什么东西？
这些节点，都有一个坐标。
这棵树就像是一棵二叉搜索树。
读者：我怎么没有看出来？
k-d tree每一层的分法是不同的。请仔细观察一下上图。对于$(7,2)$，它是以$x$坐标划分的。而对于$(5,4)$，它是以$y$坐标划分的。
可以看到，$(7,2)$左子树的$x$坐标都小于$7$，右子树的$x$坐标都大于$7$。
$(5,4)$左子树的$y$坐标都小于$4$，右子树的$y$坐标都大于$4$。
每层的划分关键字不同，这就是K-D tree的精华所在。
可以结合下图（同样来自wikipedia）理解一下。

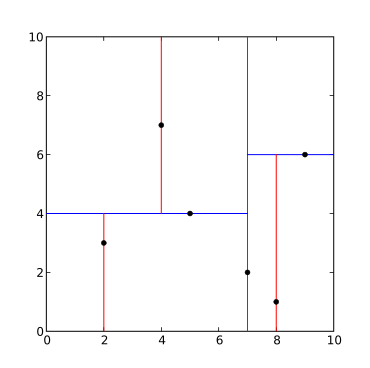
KD-tree的每棵子树都相当于一个矩形。这棵子树的根，把它划分为两个子树，也划分成两个矩形。
将K-D tree转换成图，就是一堆节点将平面划分成很多块。

K-D tree的构建

K-D tree怎么构建？
把所有的坐标列出来。
按照这一层的划分模式（$x$坐标还是$y$坐标），求出中位数（中位数不是严格意义上的，只是排序后最中间的那个。如果数组长度为偶数，那么中位数可以是中间任意一个）。将小于中位数的放在左边，将大于中位数的放在右边。以这个中位数为根。递归左右区间，作为它的左右子树。
额……讲得可能有些复杂，不过这过程真的好懂。

Build(l,r)
	以这一层的划分模式找到[l,r]区间的中位数。
	以中位数划分数组。
	新建节点，为当前子树的根。节点的坐标为中位数。
	递归数组[l,mid-1]，作为左子树。
	递归数组[mid+1,r]，作为右子树。
	维护信息。
	返回当前子树的根节点。

不会写伪代码……
这样建树的时间复杂度是$O(n\lg^2n)$的。
但是……
提前了解过的人知道，K-D tree建树还可以更快。
是什么呢？
这里就对不起Pascal选手了，因为C++有个函数，叫nth_element
是这样用的：nth_element(l,k,r,comp)
前面的三个东西是迭代器（也可以说是指针），后面是比较函数，打过快排的人都知道（当然，如果数组类型本来就有比较运算符时，可以忽略）。
这个表示在区间$[l,r)$中，找出排名为$k$的数并放在$k$这个位置。而且，将小于它的放在前面，大于它的放在后面。等于？~~（其实放在前面后面都一样）~~其实你可以理解成排序后的第$k$大，不会并列的。
这个神奇的东西，可以让我们非常容易地实现中位数的划分。
并且，它的时间复杂度期望是$O(n)$的！
原理？上网找了一下。原理类似快排，选取一个参照数，按照它来划分成左右两边，然后判断$k$在哪边，递归处理。每次处理的区间期望是之前的一半，所以复杂度期望是线性的。（不过说不定有什么奇葩数据会将其卡爆……因为上限是$O(n^2)$。但是继续用着也没关系，要相信C++内部的优化，想想快排用这么久，几乎没有炸过吧）
Pascal选手可以打一下，似乎很容易实现，如果怕被卡，那就像快排一样加$random$。
总的来说，K-D tree的建树时间是$O(n\lg n)$的。而且这样建树，树高是$\lg n$。

K-D tree的操作

查询矩形中的点数

对于K-D tree上的每个节点，维护以它为根的子树的所有点的坐标范围。也就是最小的，能够覆盖所有点的矩形。还要维护子树的大小。
查询的时候，自顶向下递归。如果当前节点的矩形和询问矩形不相交，那就退出；如果询问矩形包含当前节点的矩形，那就直接返回。否则继续递归（注意计算当前节点坐标对答案的贡献）。
这个时间复杂度是$O(kn^{1-\frac{1}{k}})$的，$k$是维度。
为什么？我不会证。
这个时间复杂度记住就好（记住是裸的这个操作是这个复杂度，有点变化没关系，比如带权，但是记住这是矩形。如果查询的是其它的东西，如三角形，不要盲目相信这个复杂度，有本事自己证出来，或者拍出来甚至是水分）。

还有其它查询吗？

当然有，比如最远点……
实际上，这些查询的操作太多了，靠的是自己对K-D tree的灵活运用。
复杂度很玄学，不好证。

插入？删除？

如果不是非常毒瘤的题目，那就不可能有这种东西。
动态K-D tree应该很少见。
但只要不是强制在线，那就可以先将所有插入的点放在一起，建一棵K-D tree。
对于每个点，都维护一个标记，表示它是否存在。还有维护其它的一些标记，如子树大小等。
重新做那些询问，如果是插入或删除，那就修改那个点的标记，然后简单粗暴地向上跳，维护信息。
反正树高是$\lg n$的，不怂。
这个思想可以用于其它的树。静态操作，无需旋转之类的东西。复杂度反正一样，常数小一些，而具体怎样要看数据（因为在某个时刻，插入的元素个数总是远远小于插入总数）。
如果真的要动态操作呢？
那就和替罪羊一样，设置一个平衡因子。如果不平衡了，那就像替罪羊那样暴力重构！

---

总结

K-D tree还是好打的。
但是那时间复杂度特别玄学啊……
会证的大佬就证，不会证的就出数据自己测，或者用来水分。