C++桶排序——详解

前言：现在中小学学习C++的人越来越多，可网上搜了搜桶排序的博文，发现大家都写得好深奥，于是，便有了这篇简单易懂(不是)的桶排序文章

 

思考一下，你面前有一些不大的数字，但是它们是乱序的，请问你如何将它们排成有序的序列？

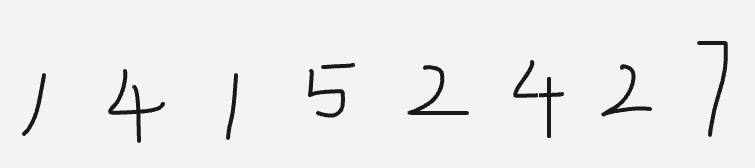
 不妨，让我们把这些数字当成生活中常见的东西，比如，这些都是不同种类的垃圾编号，我们要将这些垃圾进行分类摆放整齐，那自然的，我们需要有一些垃圾桶

可以发现，这些垃圾的编号种类不是很多，最小是1，最大是7，那么我们最多只需要准备7个垃圾桶就可以了，编号为1到7

 

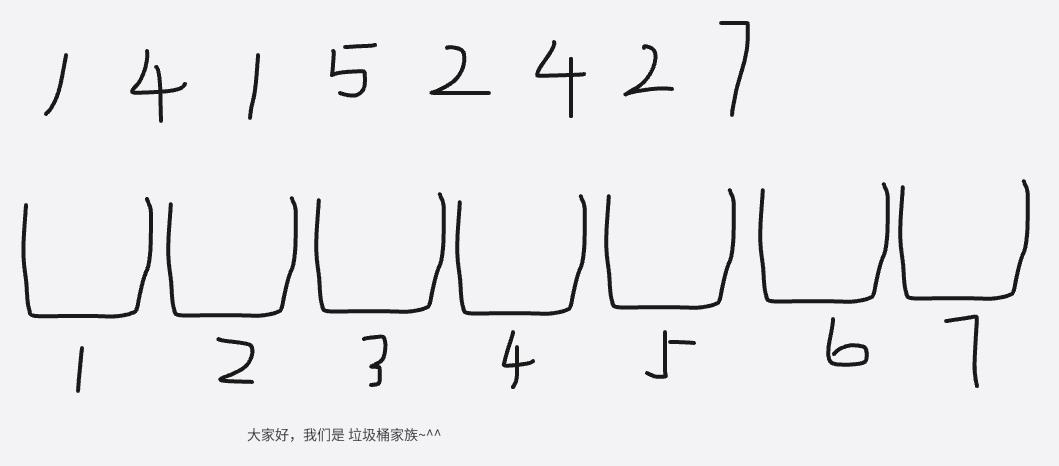
接下来，就是把每个垃圾丢到对应的垃圾桶中就可以了，然后每一个垃圾桶，就统计有多少个垃圾被丢到了这里面

 

 

 

 

 

 

 

 

 

 

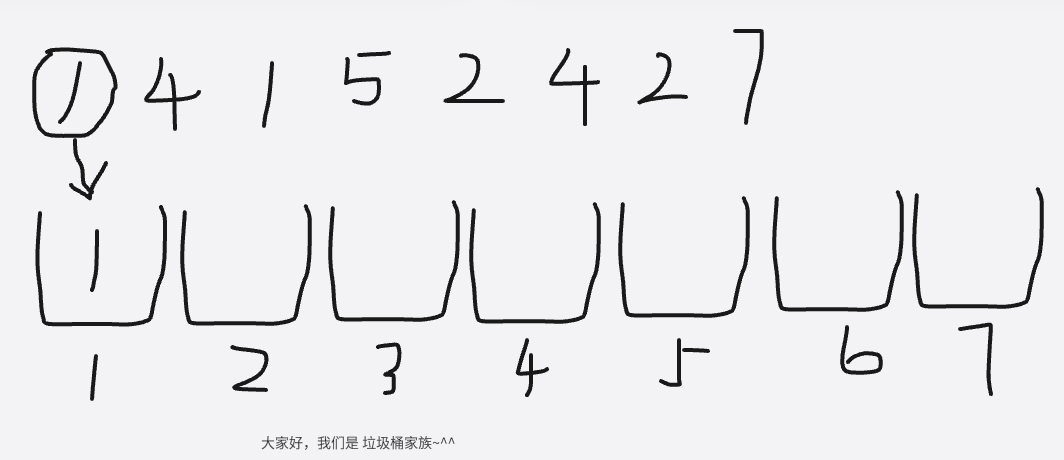
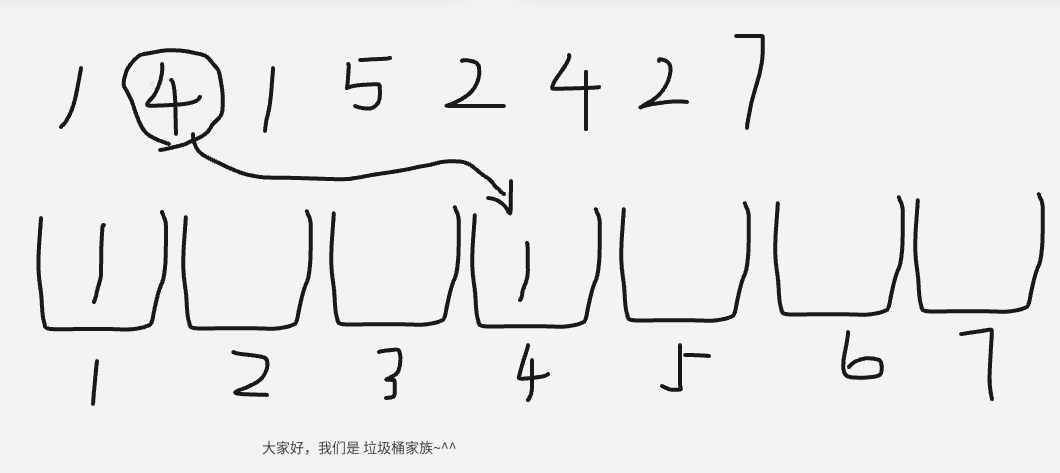
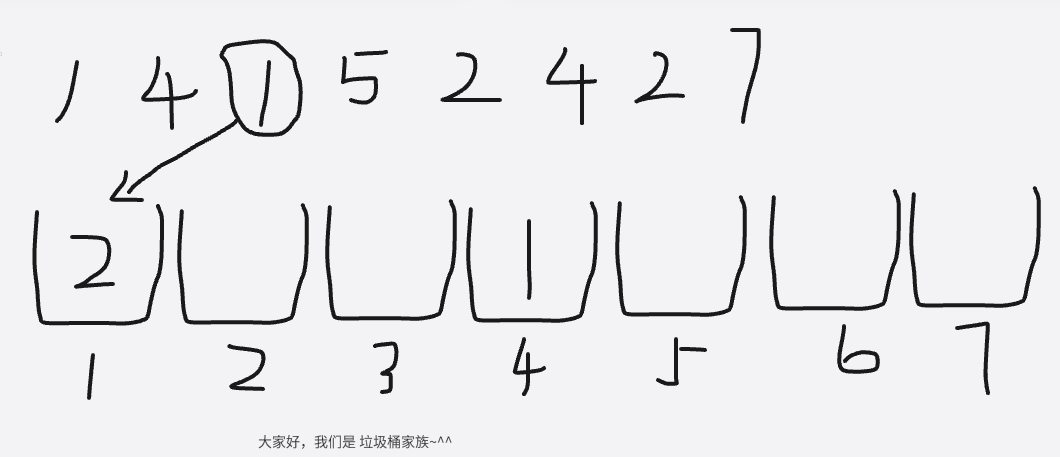
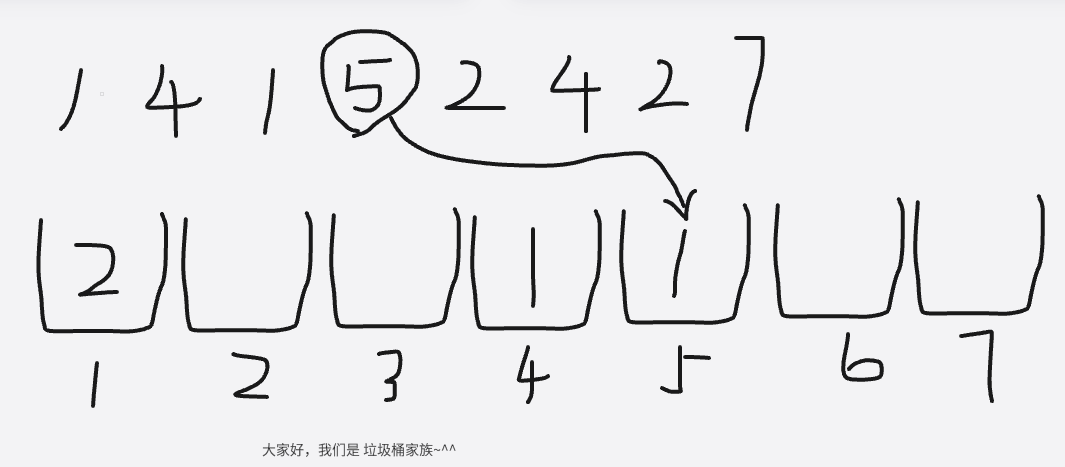
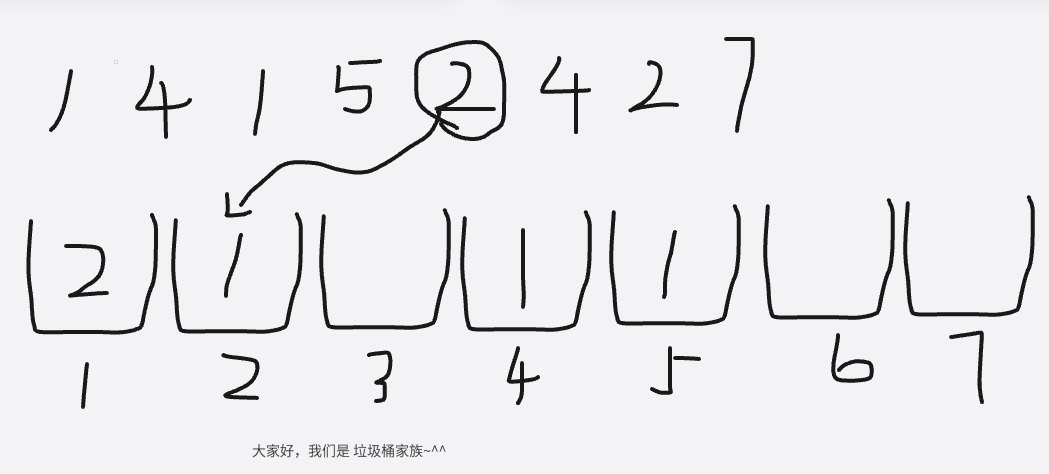
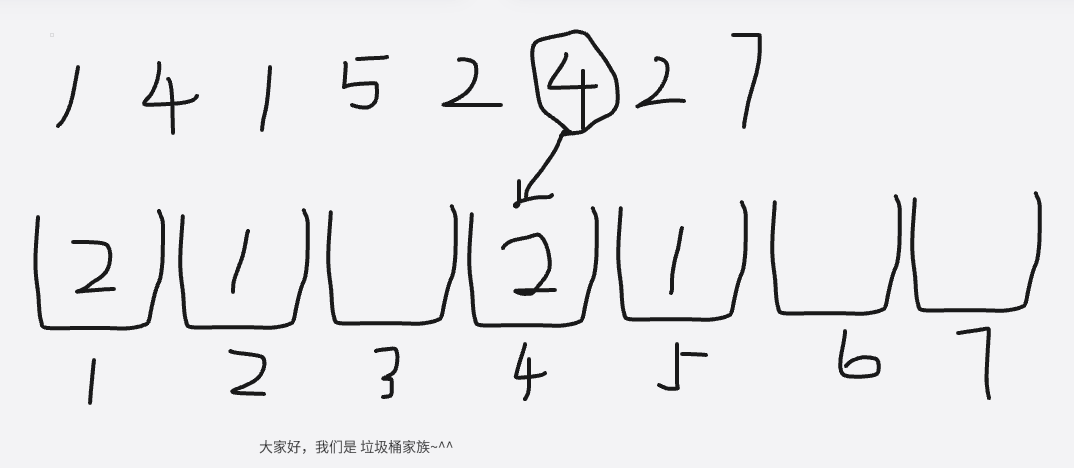
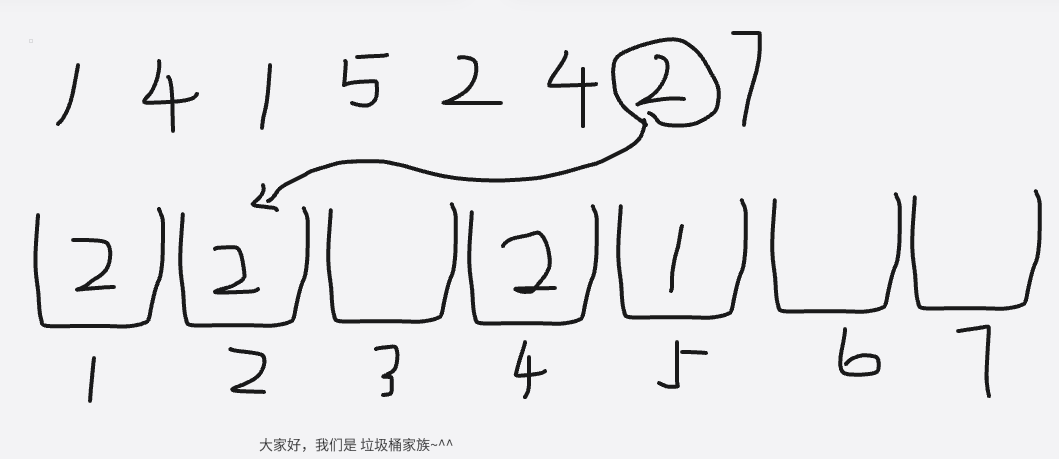
 以上就是将垃圾丢进垃圾桶的过程了，让我们回到编程中来分析一下这个过程中，我们得到了哪些数据

首先，很明显垃圾丢进垃圾桶的过程，是从左到右将垃圾依次丢入的，这符合循环的重复执行概念，所以这个过程是在循环里实现的

然后，对于循环里每一个垃圾的数值，我们设定为x； 

其次，很明显我们有7个连续的垃圾桶排放在一期，这符合数组的定义，所以我们将这7个垃圾桶定义为数组，int vis[8]，下标从1到7

思考垃圾丢进垃圾桶之前，桶应该都为空，所以vis数组应该初始化为0，表示初始时任何一个垃圾桶都没有垃圾

思考垃圾丢进垃圾桶过程中，桶里面的数字会 + 1，表示这个垃圾桶多了一个垃圾，用代码表示可以写成 vis[x] = vis[x] + 1；意为x号垃圾桶的垃圾数量加1

int main()
{
    int vis[8] = {},x,n;//vis[i]:i出现的次数 
    cin >> n;
    for(int i = 1; i <= n; i++)
    {
        cin >> x;
        vis[x]++; //x出现的次数 + 1 
    }
    return 0;
}

 

现在，让我们考虑一下按垃圾桶的顺序，依次将桶里面的垃圾全部取出，看看能不能实现排序的效果

①：vis[1] = 2，说明1号垃圾有两个，我们要取出两个1

 ②：vis[2] = 2，说明2号垃圾有两个，我们要取出两个2

③：vis[3] = 0，说明3号垃圾没出现，那就不必理会

④：vis[4] = 2，说明4号垃圾桶有两个垃圾，那就要取出两次4

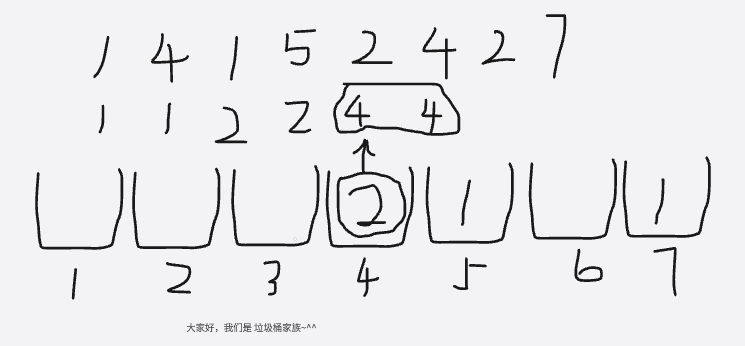
 ⑤：vis[5] = 1，说明5号垃圾桶有一个垃圾，那就要取出一次5

 

⑥：vis[6] = 0，说明6号垃圾没出现，那就不必理会

⑦：vis[7] = 1，说明7号垃圾桶有一个垃圾，那就要取出一次7

 

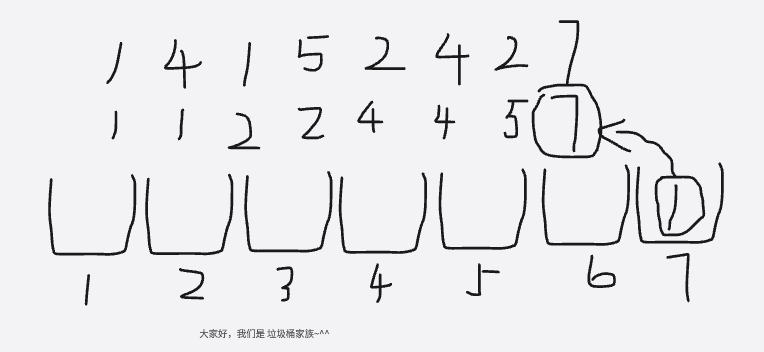
最后，来看一下程序取出桶里数字的过程

for(int i = 1; i <= 8; i++)
{
    while(vis[i] >= 1)
    {
        cout << i << " ";
        vis[i]--; //取出i，减少i出现的次数 
    }
}

输入：

8

1 4 1 5 2 5 2 7

输出：

1 1 2 2 4 5 5 7

完整代码：

#include<bits/stdc++.h>
using namespace std;

int main()
{
    int vis[8] = {},x,n;//vis[i]:i出现的次数 
    cin >> n;
    for(int i = 1; i <= n; i++)
    {
        cin >> x;
        vis[x]++; //x出现的次数 + 1 
    }
    for(int i = 1; i <= 7; i++) //桶的编号是1到7
    {
        while(vis[i] >= 1)
        {
            cout << i << " ";
            vis[i]--; //取出i，减少i出现的次数 
        }
    }
    return 0;
}

 

 

细节问题：

1.可以发现在桶存储数据的过程中出现了空桶，说明会有空间浪费的情况出现，如果在n个数据中，有数据x出现大小超过1e7(1千万)，就意味着我们要准备超过1e7个桶，这样会严重浪费系统内存，因此，桶排序只适合出现的数据都被限制在比较小的范围内的时候使用，例如最大不超过1e5或1e6

2.桶排序的时间复杂度，可以发现我们只需要一次循环n个数，就可以将每个数丢到桶里，说明这个算法只需要一重循环可以实现，对于一重循环n个数的程序，我们称其时间复杂度为O(n)，但是别忘了，桶的数量不一定是n个，设桶的数量为k个，那么在取出桶的过程中也是一个1到k的循环，为O(k)，所以整体的时间复杂度为O(n + k)，还是比较快速的