多源最短路算法——Floyd算法（转载）

1.多源最短路简介：
我们知道单源最短路是指从某一个源点到图中的其它顶点的最短路。
多源最短路就是指每一个点到图中其他顶点的最短路。
那么有的人肯定想我知道求单源最短路的算法了，那么有多少个点我就求多少次呗，这样做时间效率不高，空间效率也极其低。
那么有什么算法求解多源最短路呢？——Floyd

2.Floyd简介：

 

3.三维空间Floyd核心代码：

int g[N][N];  // 邻接矩阵存图
int dp[N][N][N];
void floyd(int n) {
    for (int k = 0; k <= n; ++k) {
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (k == 0) {
                    dp[k][i][j] = g[i][j];
                } else {
                    dp[k][i][j] = min(dp[k - 1][i][j], dp[k - 1][i][k] + dp[k - 1][k][j]);
                }
            }
        }
    }    
}

这样太浪费空间了把。

4.Floyd空间优化：

 

 

 

怎么确定状态转移的？
看下图

 

 

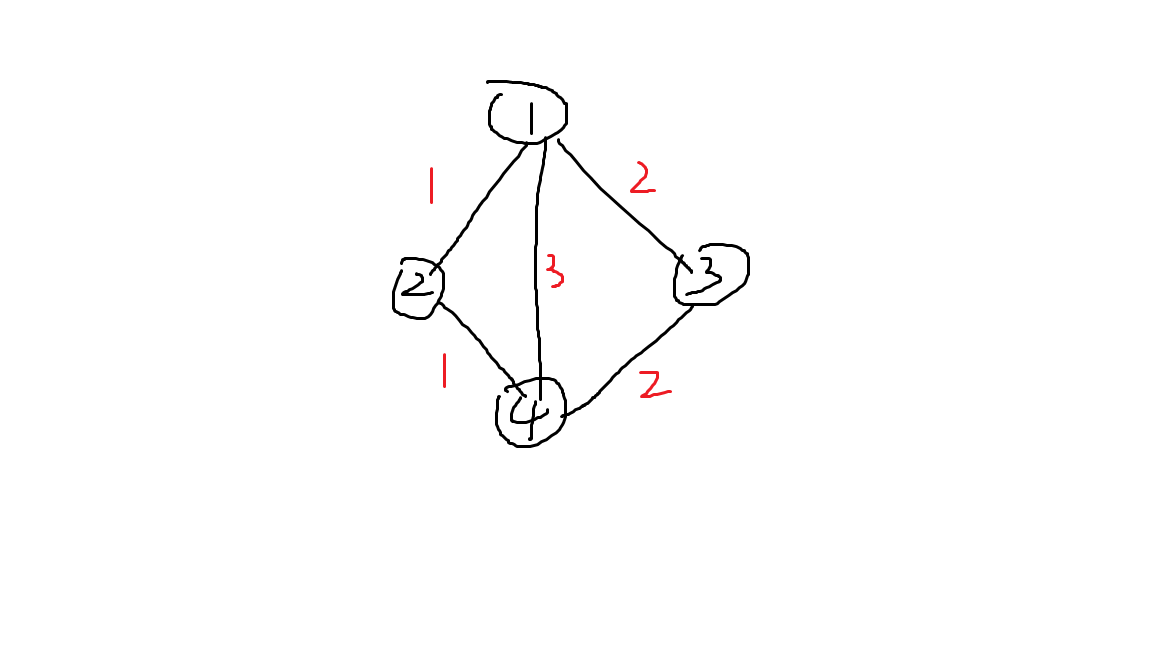
我们发现从顶点1到顶点4有三条路径
dp[0][1][4]就相当于图中的g[1][4]这里采用邻接矩阵的形式
然后k作为中介点可以使2，3
那么dp[2][1][4] = dp[2][1][2] + dp[2][2][4]
也就是我们可以简化为dp[1][4] = dp[1][2] + dp[2][4]
V1到V4等于V1到V2加上V2到V4，可以理解吧。
然后V1到V4还可以等于V1到V3加上V3到V4
即最后的最短路就是dp[1][4] = min(g[1][4], min(g[1][2] + g[2][4]
, g[1][3] + g[3][4]))

优化空间后的Code

int g[N][N];
void floyd(int n) {
    for (int k = 1; k <= n; ++k) {
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
            }
        }
    }    
}

 

8046: 校园绿化

描述

 

校园内曲径通幽、景色宜人，可tzc的同学们都很忙，为了挤出更多的时间学习，都喜欢走捷径，他们希望任意两个路口之间都能够按照最短的路线行走，以致绿化带被踩出来了很多的小路，而原本的路则可能导致无人行走。学校领导以“学生为本”尊重学生们的选择，但又想让校园更加优美，因此在保证同学们任意两个路口都能按最短的路线行走的前提下（路口要始终保留，若两个路口之间存在多条最短的路，应保留这些路段，使同学们有更多的选择），将那些没有人行走的路段还原为绿化带，现在请聪明的你把它们都找出来。

 

 

输入

 

第一行为n(2≤n≤100)和m(n-1≤m≤min(n(n-1)/2, 1000))，n表示路口数量，m表示直接连接两个路口的路段数量，每个路口从1到n编号。
之后有m行，每行三个正整数u，v，w，表示从路口u到路口v之间有一段直接相连的路（不经过其它路口）(1≤u, v≤n, u≠v，1≤w≤1000)，任意两个路口之间只有一个路段。

数据保证任意两个路口之间能有路可走（可以间接）。

 

 

输出

 

按照输入的先后顺序输出可以还原为绿化带的直接连接两个路口的所有路段，每行一项。

每个路段包括3个数据u, v, w，与输入信息一致。

如果不存在，则输出None

 

 

样例输入

 

3 3
1 2 1
1 3 1
2 3 3

 

样例输出

2 3 3

#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
const int inf = 1e9+10; 
struct node{
    int x,y,t;
};
node a[N];
int g[N][N];
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            g[i][j] = g[j][i] = inf;
    for(int i=1;i<=m;i++)
    {
        int x,y,t;
        cin>>x>>y>>t;
        if(t<g[x][y])g[x][y] = g[y][x] = t;
        a[i].x = x;a[i].y = y;a[i].t = t;
    }
    for(int k = 1;k<=n;k++)
        for(int i = 1;i<=n;i++)
            for(int j = 1;j<=n;j++)
                if(g[i][j]>g[i][k]+g[k][j])
                    g[i][j] = g[i][k]+g[k][j];
    int ans = 0;
    for(int i=1;i<=m;i++)
    {
        int x = a[i].x,y = a[i].y,t = a[i].t;
        if(g[x][y]<t){
            printf("%d %d %d\n",x,y,t);
            ans++;
        }
    }
    if(!ans)cout<<"None";
     return 0;
}

 

 转载自：https://blog.csdn.net/lytwy123/article/details/90214622