周六900C++班级-2022-11-19 01背包

背包问题关系图

 

 

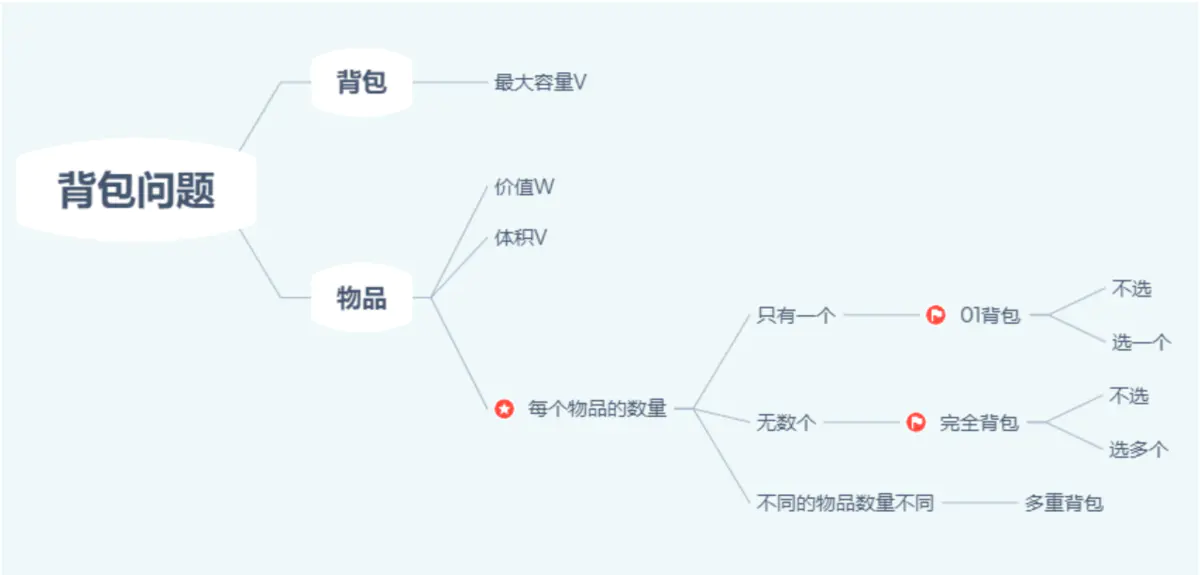
问题描述

若有 N 件物品和一个最多能装重量为 W 的背包，一个物品只有两个属性：重量和价值。第i件物品的重量是weight[i]，得到的价值是value[i] 。假设每件物品只能用一次，将哪些物品装入背包里物品价值总和最大？

注意：0-1 背包问题无法使用贪心算法来求解，也就是说，不能按照先添加性价比最高的物品来达到最优，因为这种方式可能造成背包空间的浪费，从而无法达到最优。

 

 

基本思路

上述问题是典型的动态规划，这里有两个可变量：重量和价值，我们定义dp[i][j]：前i件物品重量不超过j时背包能达到的最大价值，背包的初始状态是最终目标是dp[N][W]，即前N件物品重量不超过W时背包能达到的最大价值。

设第 i 件物品重量为 w，价值为 v，根据第 i 件物品是否添加到背包中，可以分两种情况讨论：

• 第 i 件物品没添加到背包，最大价值：dp[i][j] = dp[i - 1][j]。
• 第 i 件物品添加到背包中：dp[i][j] = dp[i - 1][j - w] + v。

第 i 件物品可添加也可以不添加，取决于哪种情况下最大价值更大。因此，0-1 背包的状态转移方程为：
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w] + v)

#include<bits/stdc++.h>
using namespace std;
int dp[30][30005];
int n,m;
int w[30],v[30];//w重量,v价值 
int main()
{
    cin>>m>>n;
    for(int i=1;i<=n;i++)
    {
        int x,y;
        cin>>x>>y;
        w[i] = x; //重量 = 价钱 
        v[i] = x*y; //价值 = 价钱x*重要度y 
    }
    //以下是01背包环节
    for(int i=1;i<=n;i++) //先循环物品
    {
        for(int j=1;j<=m;j++) //再循环容量
        {
            if(j-w[i]>=0) 
                dp[i][j] = max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
            else //不能取第i个物品时的最大值与上一层i-1相同
                dp[i][j] = dp[i-1][j];
        } 
    } 
    cout<<dp[n][m];
     return 0;
}

 优化

由于dp[i][j]的值只与dp[i-1][0,...,j-1]有关，可以采用动态规划常用的优化方法对空间进行优化（即去掉dp的第一维）。因此，0-1 背包的状态转移方程为： dp[j] = max(dp[j], dp[j - w] + v)

特别注意：为了防止上一层循环的dp[0,...,j-1]被覆盖，循环的时候 j 只能逆向遍历。优化空间复杂度：

#include<bits/stdc++.h>
using namespace std;
int dp[30005]; //优化后dp数组为最大背包容量 
int n,m;
int w[30],v[30];//w重量,v价值 
int main()
{
    cin>>m>>n;
    for(int i=1;i<=n;i++)
    {
        int x,y;
        cin>>x>>y;
        w[i] = x; //重量 = 价钱 
        v[i] = x*y; //价值 = 价钱x*重要度y 
    }
    //以下是01背包环节
    for(int i=1;i<=n;i++) //先循环物品
    {
        for(int j=m;j>=w[i];j--) //再循环容量，一维背包为防止覆盖先前数据要逆序循环 
        {
            dp[j] = max(dp[j],dp[j-w[i]]+v[i]); //一维背包的状态转移方程 
        } 
    } 
    cout<<dp[m];
     return 0;
}

01背包内循环理解：还原成二维的dp就很好理解，一维的dp是二维dp在空间上进行复用的结果。dp[i]=f(dp[i-num])，等式的右边其实是二维dp上一行的数据，应该是只读的，在被读取前不应该被修改。如果正序的话，靠后的元素在读取前右边的dp有可能被修改了，倒序可以避免读取前被修改的问题。

完全背包

#include<bits/stdc++.h>
using namespace std;
int dp[30][30005]; //dp[i][j] = 前i个物品组合且最大容量为j时的最大价值
int n,m;
int w[105],v[105];//w重量,v价值 
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>w[i];
    for(int i=1;i<=n;i++)
    {
        dp[i][0] = 1; //初始化方案数为1 
        for(int j=0;j<=m;j++)
        {
            if(j-w[i]>=0) //dp[i][j] = 不取第i个物品的最大值dp[i-1][j] + 取第i个物品dp[i][j-w[i]] 
                dp[i][j] = dp[i-1][j] + dp[i][j-w[i]];  
            else 
                dp[i][j] = dp[i-1][j];
        }
    }
    cout<<dp[n][m];
    return 0;
}

 完全背包，优化

#include<bits/stdc++.h>
using namespace std;
int dp[30005]; //dp[j] = 最大容量为j时的最大价值
int n,m;
int w[105],v[105];//w重量,v价值 
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>w[i];
    for(int i=1;i<=n;i++)
    {
        dp[0] = 1; //初始化方案数为1 
        for(int j=w[i];j<=m;j++)
        {    //dp[i][j] = 不取第i个物品的最大值dp[i-1][j] + 取第i个物品dp[i][j-w[i]] 
            dp[j] = dp[j] + dp[j-w[i]];  
        }
    }
    cout<<dp[m];
    return 0;
}