Knowledge 1：Propositional Logic 命题逻辑基础及符号

Keywords

• reasoning 推理
• Deductive reasoning(for a basic logic) 演绎推理
• analogy 类比；比喻 /əˈnælədʒi/ 
• definition of terminology  /ˌtɜːmɪˈnɒlədʒi/术语的定义
• proposition/ˌprɒpəˈzɪʃn/命题
• distinction/dɪˈstɪŋkʃn/n. 区别；差别
• arithmetic /əˈrɪθmətɪk/ 算术，算法
• anthropomorphize/,ænθrəpəʊ'mɔːfaɪz/vt. 赋与人性，人格化
• knowledge base(KB) 知识库
• connectionism /kə'nekʃənizəm/ 联结主义
• retrieval /rɪˈtriːvl/n. 检索；恢复；取回；拯救
• inference: 推理
• entailment：蕴含
• syntax:  /ˈsɪntæks/n. 语法；句法；
• semantic: /sɪˈmæntɪk/adj. 语义的；语义学的
• falsity: /ˈfɔːlsəti/n. 虚伪；错误；谎言；不真实
• notation /nəʊˈteɪʃn/n. 符号
• terminology：/ˌtɜːmɪˈnɒlədʒi/n. 术语，术语学；用辞
• theorem/ˈθɪərəm/n. [数] 定理；原理
• axiom: /ˈæksiəm/n. [数] 公理
• iff: 当且仅当
• K |= a是语义蕴含，K |- b是形式推演

 

What's all the Fuss about?

• Resources required to solve a problem
• Time(computational complexity)
• Memory
• Some problem are easy to solve
• 1+1=?
• This is good!
• Some problems are difficult to solve
• Playing chess, scheduling/timetabling...
• Is this bad?
• Some problems cannot be solved!
• Reasoning, planning,...

 

What is knowledge?

• taking the world to be one way and not another
• the propositions for the true or false encode what you know about the world.

 

What is representation?

• symbolic encoding of propositions believed by some agent 命题的符号编码，由某些行为者相信
• symbols standing for things in the world

 

What is reasoning?

• Manipulation of symbols encoding propositions to produce representations of new propositions.对编码命题的符号进行操作，以产生新命题的表示。

 

Why knowledge?

• taking an intentional stance

 

Why representation?

• intentional stance says nothing about what is / is not represented symbolically

 

Why reasoning?

• Want knowledge to affect action
• We don't want to do action A if sentence P is in KB,
• But rather do action A if world believed in satisfies P
• Difference:
• P may not be explicitly represented
• Need to apply what is known to particulars of given situation
• Usually need more than just DB-style retrieval of facts in the KB

 

Entailment

• Sentences P1, P2, ..., Pn entail sentence P iff the truth of P is implicit in the truth of P1, P2, ..., Pn
• Inference: the process of calculating entailments
• sound: get only entailment
• complete: get all entailment
• Sometimes want unsound / incomplete reasoning
• Logic: study of entailment relations

 

Using Logic

• No universal language / semantics
• No universal reasoning scheme
• Start with first-order predicate calculus(FOL)

 

Why do we need formal Knowledge Representation?

• Natural languages exhibit ambiguity
• ambiguity make it difficult to make any inferences

 

Syntax vs Semantics

• Syntax: Describe the legal sentences in a knowledge representation language.
• Semantics: Refers to the meaning of sentences. Semantics talks about truth and falsity.

 

Propositions

• Propositions are statements of fact.
• We shall use single letters to represent propositions
• P: Socrates is bald.

 

Formulae in Propositional Logic

 

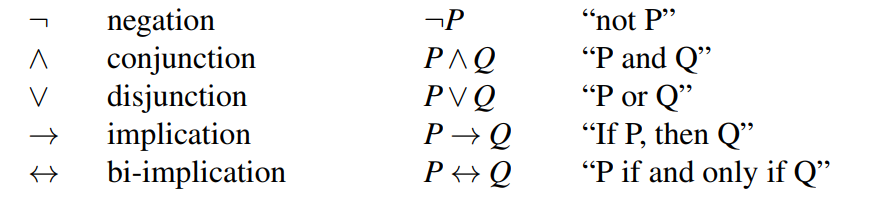
Syntax

• BNF grammar
• Sentence ::= AtomicSentence || ComplexSentence
• AtomicSentence ::= True || False || P || Q || R || . .
• ComplexSentence ::= ( Sentence ) || Sentence Connective Sentence || ¬ Sentence
• Connective ::= ∧ || ∨ || → || ↔

 

Semantics

• The semantics of the connectives can be given by truth tables. It determines the semantics for complex formulae.

 

 

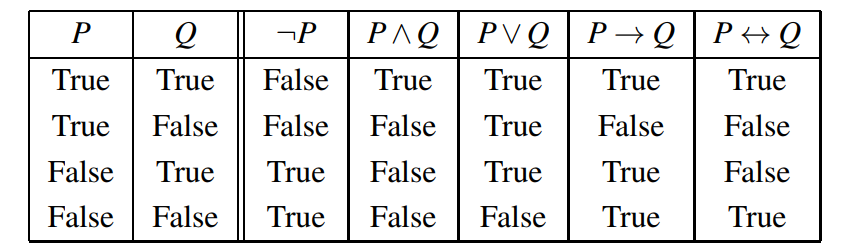
What is a logic?

• A logic consists of:
• A formal system for expressing knowledge about a domain consisting of
• Syntax: Sentences(well formed formulae)
• Semantics: Meaning
• A proof theory: rules of inference for deducing sentences from a knowledge base

 

Provability

• λ ⊢ ρ: we can construct a proof for ρ from λ using axioms and rules  of inference
• If λ is empty (i.e., 0⊢ρ) and ρ is a single formula, then we say that ρ is a theorem of the logic

 

Entailment

• λ |= ρ: whenever the formula(s) λ are true, one of the formula(s) in ρ is true
• In the case where ρ is a single formula, we can determine whether  λ |= ρ by constructing a truth table for λ and ρ. If, in any row of the  truth table where all the formulae in λ are true, ρ is also true, then  λ |= ρ.
• If λ is empty, we say that ρ is a tautology

 

Soundness and Completeness

• λ |= a是语义蕴含， λ |- b是形式推演
• An inference procedure (and hence a logic) is sound if and only if it  preserves truth
• In other words ⊢ is sound iff whenever λ ⊢ ρ, then λ |= ρ
• Soundness 是说右侧推演的知识都是被λ蕴含的（推出来的知识都是正确的）
• A logic is complete if and only if it is capable of proving all truths
• In other words, whenever λ |= ρ, then λ ⊢ ρ
• Completeness 是说，左侧蕴含出来的知识都可以推演出来
• A logic is decidable if and only if we can write a mechanical procedure (computer program) which when asked λ ⊢ ρ it can eventually halt and answer “yes” or answer “no”