[Leetcode 189]轮转数组

Leetocde189 轮转数组

这题能被用做mid题是因为一题多解，其中基于双指针的轮状数组解法是比较难的

1. 使用新数组

__直接把第i个元素移到第（i+k）%numsize位置，类似循环队列

void rotate(int* nums, int numsSize, int k) {
    int newArr[numsSize];
    for (int i = 0; i < numsSize; ++i) {
        newArr[(i + k) % numsSize] = nums[i];
    }
    for (int i = 0; i < numsSize; ++i) {
        nums[i] = newArr[i];
    }
}

2. 数组翻转+双指针

这种解法上次是在王道考研数据结构里面见过

一共进行三次翻转

class Solution {
public:
    //编写翻转函数
    void reverse(vector<int>& nums, int start, int end) {
        while (start < end) {
            swap(nums[start], nums[end]);
            start += 1;
            end -= 1;
        }
    }
    //分别进行三次翻转
    void rotate(vector<int>& nums, int k) {
        k %= nums.size();
        reverse(nums, 0, nums.size() - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, nums.size() - 1);
    }
};

3. 轮转数组

最优但是不好理解
这种解法是因为，只要确定了k值，实际上就可以直接确定某个元素移动之后下一个位置了，但是有些时候再次回到起点时，会陷入循环（此时还有未访问的元素），所以要从另一个新的起点出发循环
所以总的过程需要两个循环。内层循环还是比较简单的

主要难点是如何确定外层循环的次数？

两种解决方法

1. 再定义一个变量，用来统计访问到的元素次数，只要访问完所有元素，整个过程就结束了

2. 数学公式推导
   YYSY，这个推导我想了很久才想明白。

关键是我们想要知道的是外层循环要多少次

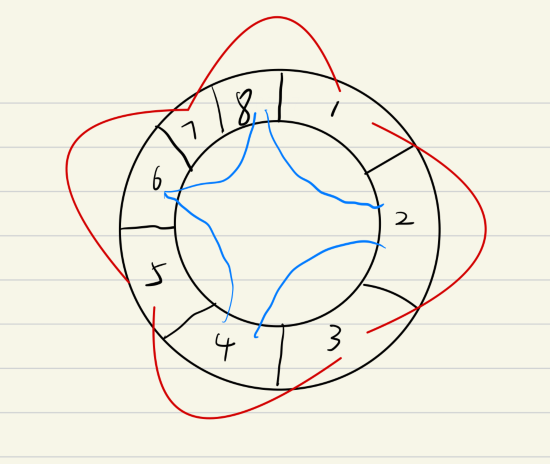
如果我们知道一次小循环/内层循环(上图红色、蓝色分别为一个小循环)走过的元素个数，那么外层循环只需要总元素个数n/内层元素个数就能计算出来了，不妨设内层小循环访问的元素个数为b

那么完成一次小循环走过的总步长为BK

又因为，从起点又回到终点，等价于一步一步走，走了n步，回到原点。那么一定存在一个整数a，使得an=bk。

---

如果还不好理解，就看这个例子

把环状数组想象成无限长的重复数列

• [··· 1,2,3,4,1,2,3,4···]
  k=2: 1->3->1,此时一个小循环只有两个元素，b=2,n=4 ==>a=1

• [···1,2,3,4,5,1,2,3,4,5,1···]
  k=2: 1->3->5->2->4->1 此时一个小循环中，b=5,n=5 ==>a=2