【ACWING】模拟单链表、双链表、栈、队列、堆、哈希表

1 模拟链表

讲讲用数组模拟链表

1. 单链表
2. 双链表

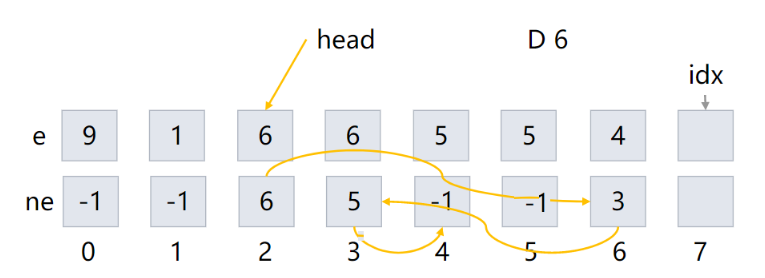
开两个数组e[N],ne[N]，前者存值，后者指向下一个节点，相同下标的对应同一个节点。

比如e[i],ne[i]，分别表示节点i的值，以及节点i指向下一个节点，ne[i]存的是下一个节点的index

初始化一个idx变量用于索引和存储，idx不断++，虽然元素是在数组中一个个存的，看起来是连续的，但是实际上链表会如下图所示

2 模拟栈

1. 模拟栈

int stk[N];
int tt = -1;  // top
 
void push(int x){
	stk[++tt] = x;
}
 
void pop(){
	tt --;
}
 
int query()
{
    // 求栈顶元素
    return stk[tt];
}
 
void empty()
{
	if(tt==-1)
	{
		cout<<"YES"<<endl;
	}else{
		cout<<"NO"<<endl;
	}
}

3 模拟队列

1. 模拟队列

int q[N];
int m,hh=0,tt=-1;
 
void push(int x)
{
    q[++tt] = x;
}
 
void pop()
{
    hh ++;
}
 
bool empty()
{
    if(tt<hh){
        return true;
    }
    return false;
}
 
int query(){
    return q[hh];
}

4 模拟堆

小根堆（小顶堆）：每一个节点，小于等于左右儿子

堆的存储：用一维数组来存，一个节点为x，则左儿子为2x，右儿子为2x+1 ->完全二叉树序号定义 下标从1开始

// 核心操作 上筛和下筛
void down(int u)	// 输入父节点下标，比较该父节点和左右儿子的大小，取最小的替换父节点
{
	int t = u;	// 暂定最小的是输入的父节点
	if(u * 2 <= hsize && h[u * 2] < h[t]) t = u * 2;	// 如果有左儿子，且左儿子更小，则修改
	if(u * 2 + 1<= hsize && h[u * 2 + 1] < h[t]) t = u * 2 + 1;	// 如果有右儿子，且右儿子更小
	
    // 如果发生了变化，则让儿子替换父节点，然后继续下筛
	if(u != t){
		mySwap(u,t);
		down(t);
	}
}
 
void up(int u)
{
    // 如果存在父节点u/2 且 父节点大于儿子节点，交换。
	while(u/2 && h[u/2] > h[u]){
		mySwap(u/2,u);
		u /= 2;	// 继续上筛
	}
}

5 模拟哈希表

1. 哈希表的用途：将一个大的范围的数，映射到一个小范围

   一般涉及 插入 和 查找 两个操作，查找接近O（1）

2. 哈希函数：(x % N + N) % N （取模的时候N常用质数）, 如果是负数的话也能映射到N这个区间内

3. 冲突处理

   1. 拉链法
   2. 开放地址法（只需要一个数组，但是数组长度要开到题目范围的2/3倍）

5.1 拉链法

//哈希表h[N]，每一项对应一个链表。这里的写法是多个链表共享一个一维数组e[N],ne[N]
int h[N], e[N], ne[N], idx;
 
// 插入x，找到位置k后，写入对应的链表中
void insert(int x){
    int k = ((x%N)+N)%N;
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx++;
}
 
// 查找的时候直接遍历对应的链表
bool find(int x){
    int k = ((x%N)+N)%N;
    for(int i = h[k]; i!= -1; i =ne[i]){
        if (e[i] == x) return true;
    }
    return false;
}
 

5.2 开放地址法

// 用null表示一个还未存储的空位
const int N = 200003, null = 0x3f3f3f3f;
int h[N];
 
// 如果找到x，返回下标，如果没有找到x，返回x应该存到的地方
int find(int x )
{
    int k = (x % N + N) % N ;
    while(h[k]!= null && h[k]!=x){
        k++;
        if(k == N) k = 0;
    }
    return k;
}