数理统计12：枢轴量法、分位数、正态参数区间估计

上篇文章中，我们探讨了区间估计的相关基本概念，也提出了Neyman置信区间，今天我们将聚焦于如何寻找置信区间的问题上，并对最常用的总体：正态总体给出一些置信区间的找法。为了方便起见，以下我们都让置信水平为\(1-\alpha\)。

由于本系列为我独自完成的，缺少审阅，如果有任何错误，欢迎在评论区中指出，谢谢！

目录

• Part 1：枢轴量法
• Part 2：分位数
• Part 3：单正态总体参数区间估计
  • 1、\(\sigma^2\)已知时\(\mu\)的区间估计
  • 2、\(\sigma^2\)未知时\(\mu\)的区间估计
  • 3、\(\mu\)未知时\(\sigma^2\)的区间估计
  • 4、\(\mu\)已知时\(\sigma^2\)的区间估计
• Part 4：双正态总体参数区间估计
  • 1、均值差\(\mu_2-\mu_1\)的区间估计
  • 2、方差比\(\sigma_2^2/\sigma_1^2\)的区间估计

Part 1：枢轴量法

枢轴变量法是基于点估计量的。我们知道，统计量是样本的函数，这意味着统计量中不能含有未知参数，而参数的点估计量是用统计量的观测值作为待估参数的估计值，其分布一定含有待估参数，枢轴量法的思想就是，通过一定的变换，让点估计的函数的分布不含待估参数，进而基于分布来构造区间估计。

举一个简单的例子，对于正态总体\(N(\mu,4)\)，显然\(\bar X\sim N(\mu,4/n)\)，这里\(\bar X\)的分布含有未知参数\(\mu\)。构造其枢轴量，就是找到一个函数变换，使得新的随机变量分布不含未知参数。注意，这里用了随机变量这个词而不是统计量，意味着枢轴量不是统计量，即不能由样本观测值计算出，这是因为虽然枢轴量的分布不含未知参数，但是枢轴量的表现形式含有未知参数。显然，这里

\[\bar X-\mu\sim N(0,\frac{4}{n}), \]

这样，\(\bar X-\mu\)的分布已知，自然容易找到一个常数区间\([c,d]\)，使得这个区间有\(1-\alpha\)的概率包含\(\bar X-\mu\)的观测值，虽然此时我们不知道区间的端点是多少，但至少知道端点可以是固定的数\(c,d\)。对枢轴量使用不等式变换，即\(\bar X-\mu\in[c,d]\Rightarrow \mu\in[\bar X-d,\bar X-c]\)，得到置信水平为\(1-\alpha\)的置信区间。这就是枢轴量法的操作步骤。

不同分布族的参数对于总体的意义是不同的。像正态分布\(N(\mu,\sigma^2)\)的均值\(\mu\)，均匀分布\(U(a,a+r)\)的起点\(a\)这种参数主要影响观测值的大小，可以直接通过\(X-\mu\)，\(X-a\)的手段消除，这种参数称为位置参数；正态分布\(N(\mu,\sigma^2)\)的标准差\(\sigma\)，指数分布\(E(\lambda)\)的速率\(\lambda\)这种参数主要影响观测值的离散程度，可以通过\(X/\sigma\)，\(\lambda X\)之类的手段消除，这种参数称为尺度参数。面对不同的参数，往往有不同的方式构造枢轴量，应当结合其特点选择构造方式。

接下来，我们将枢轴量法运用到一些具体实例中，体会枢轴量法的实际应用。

Part 2：分位数

在开始枢轴量法的实际应用前，先介绍分位数这一概念，这为我们确定置信区间提供了有力武器。现在，我们先给出分位数的定义（如果不特别说明，都指总体分位数而非样本分位数）。分位数可以分为下分位数和上分位数，一般称下分位数为分位数，但我们更常用的是上分位数。

对于某个分布\(F\)，\(X\sim F\)，\(F\)的（下）\(\alpha\)分位数指的是这样一个点\(x_\alpha\)，满足

\[\mathbb{P}(X\le x_\alpha)=\alpha, \]

如果\(F\)有反函数\(F^{-1}(x)\)，则有\(x_\alpha=F^{-1}(\alpha)\)。

对于某个分布\(F\)，\(X\sim F\)，\(F\)的上\(\alpha\)分位数指的是这样一个点\(y_\alpha\)，满足

\[\mathbb{P}(X\ge y_\alpha)=\alpha. \]

换言之，如果分布函数\(F\)存在反函数\(F^{-1}(x)\)，则\(F\)的上\(\alpha\)分位数是\(y_\alpha=F^{-1}(1-\alpha)\)。

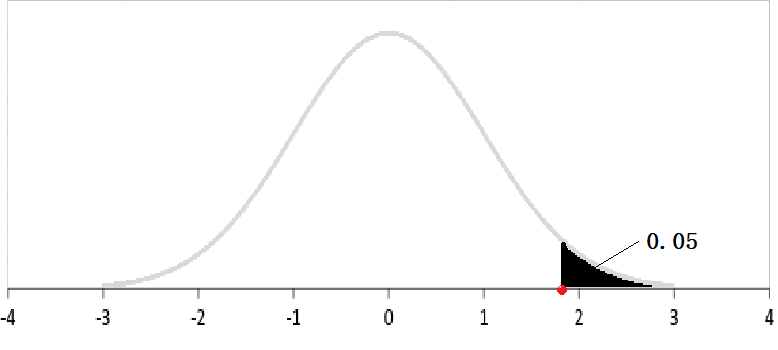
也许结合图形会更好理解。对于上面的图形，如果这是一个密度函数，黑色部分的面积为\(0.05\)，那么红色的点就是该分布的上\(0.05\)分位数，同时也是其下\(0.95\)分位数。

显然，对于一个完全确定的分布，其各分位数都是完全确定的，是常数。分布多种多样，不可能对所有分布都详细地讨论其分位数，但是对一些常用分布，其各分位数的数值已经被制成表，这包括标准正态分布，与正态分布的三大衍生分布——\(\chi^2\)分布、\(t\)分布、\(F\)分布。

今后，我们将使用\(u_\alpha\)、\(\chi^2_\alpha(n)\)、\(t_\alpha(n)\)、\(F_{\alpha}(m,n)\)，分别代表标准正态分布、自由度为\(n\)的\(\chi^2\)分布、自由度为\(n\)的\(t\)分布、自由度为\(m,n\)的\(F\)分布的上\(\alpha\)分位数，给定分布类型、分位、自由度后，这些值都可以通过查阅分位数表得到。

Part 3：单正态总体参数区间估计

正态分布参数的区间估计，主要是对\(\mu\)和\(\sigma^2\)给出区间估计。其中，对\(\mu\)的估计又要分成\(\sigma^2\)已知和未知两种情况。不过，大家已经知道，与参数\(\mu\)关联最紧密的点估计是\(\bar X\)，与参数\(\sigma^2\)关联最紧密的点估计是\(S^2\)，因此枢轴量法也一定围绕着它们作文章。

事实上，只要是均值，基本都可以转化为一个正态分布；只要是方差，基本上都可以转化为一个卡方分布。然后，根据\(t\)分布和\(F\)分布的构造方式，就能构造出服从这四种分布的枢轴量来。

1、\(\sigma^2\)已知时\(\mu\)的区间估计

当\(\sigma^2\)已知时，

\[\bar X\sim N(\mu,\sigma^2), \]

枢轴量显然是\(\bar X-\mu\sim N(0,\sigma^2/n)\)，已经由此确定了一个已知分布，但是为了写出区间估计的具体表达，我们还应当将这个已知的正态分布，转化为标准正态分布。为此，我们选择枢轴量为

\[\frac{\sqrt{n}(\bar X-\mu)}{\sigma}\sim N(0,1), \]

找一个以\(1-\alpha\)概率涵盖标准正态分布观测的区间，自然会找到

\[[-u_{\alpha/2},u_{\alpha/2}], \]

即

\[-u_{\alpha/2}\le \frac{\sqrt{n}(\bar X-\mu)}{\sigma}\le u_{\alpha/2}, \]

进行恒等变换，就得到了\(\mu\)的\(1-\alpha\)置信区间为

\[\bar X-\frac{\sigma}{\sqrt{n}}u_{\alpha/2}\le \mu\le \bar X+\frac{\sigma}{\sqrt{n}}u_{\alpha/2},\\ \left[\bar X-\frac{\sigma}{\sqrt{n}}u_{\alpha/2},\bar X+\frac{\sigma}{\sqrt{n}}u_{\alpha/2} \right]. \]

2、\(\sigma^2\)未知时\(\mu\)的区间估计

当\(\sigma^2\)未知时，我们不能顺利地将\(\bar X\)标准化，但应该容易想到，用\(S^2\)替代\(\sigma^2\)能起到类似的效果，也就是构造这样的变量：\(\sqrt{n}(\bar X-\mu)/S\)。

神奇的是，\(\frac{\sqrt{n}(\bar X-\mu)}{S}\)可以被改写成\(\chi^2\)分布的形式：

\[\frac{\sqrt{n}(\bar X-\mu)}{S}=\frac{\frac{\sqrt{n}(\bar X-\mu)}{\sigma}}{\sqrt{\frac{(n-1)S^2}{\sigma^2}/(n-1)}}\stackrel{d}=\frac{N(0,1)}{\sqrt{\chi^2(n-1)/(n-1)}}\sim t(n-1), \]

因此，自然可以找到一个区间\(\frac{\sqrt{n}(\bar X-\mu)}{S}\in[-t_{\alpha/2}(n-1),t_{\alpha/2}(n-1)]\)，因此得到\(\mu\)的\(1-\alpha\)置信区间为

\[\left[\bar X-\frac{S}{\sqrt{n}}t_{\alpha/2}(n-1),\bar X+\frac{S}{\sqrt{n}}t_{\alpha/2}(n-1) \right]. \]

用R语言进行模拟，现在我们每次生成10个服从\(N(5,9)\)的简单随机样本，这一组样本可以生成一个对应的\(95\%\)置信区间（假设\(\sigma^2=9\)是未知的）。进行10000次试验，生成10000个这样的区间，观察这个区间会涵盖待估参数\(\mu=5\)多少次。

rm(list = ls())  # 清空工作区
dev.off()  # 清空图形区

n <- 10
t <- qt(0.975, df=n-1)  # t的上0.025分位数
upper.bound <- c()
lower.bound <- c()

for (j in 1:10000){
  xlst <- rnorm(10, 5, 3)
  M <- mean(xlst)
  S <- sqrt(var(xlst))
  upper.bound[j] <- M+S*t/sqrt(n-1)
  lower.bound[j] <- M-S*t/sqrt(n-1)
}

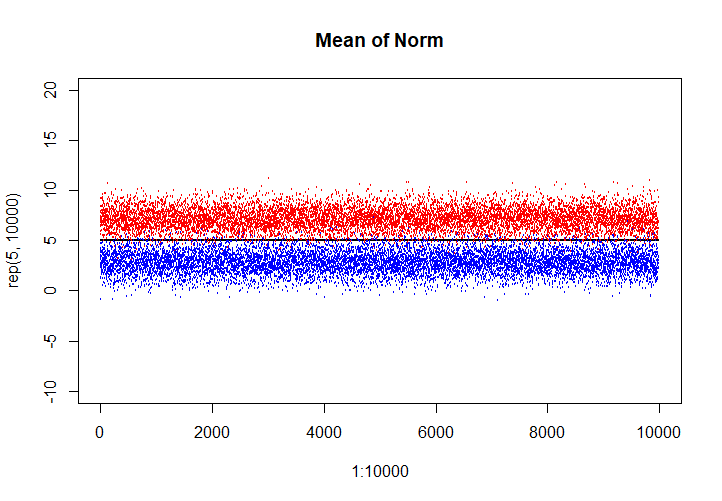
plot(1:10000, rep(5, 10000), main = "Mean of Norm", ylim = c(-10, 20), cex=0.1)
points(1:10000, upper.bound, col='red', cex=0.1)
points(1:10000, lower.bound, col='blue', cex=0.1)
sum(upper.bound < 5 | lower.bound > 5)  # 输出区间不涵盖待估参数的次数

输出结果为，10000次中，有384次没有涵盖待估参数，图示如下：

3、\(\mu\)未知时\(\sigma^2\)的区间估计

我们在给出\(S^2\)的分布信息时，实际上已经构建出了枢轴量：

\[\frac{(n-1)S^2}{\sigma^2}\sim \chi^2(n-1). \]

所以我们可以给出相应的\(1-\alpha\)概率区间，不过要注意的是\(\chi^2\)分布不像正态分布、\(t\)分布一样，是对称分布，所以概率区间为\(\frac{(n-1)S^2}{\sigma^2}\in[\chi^2_{1-\alpha/2}(n-1),\chi^2_{\alpha/2}(n-1)]\)，得到\(\sigma^2\)的置信区间为

\[\left[\frac{(n-1)S^2}{\chi^2_{\alpha/2}(n-1)},\frac{(n-1)S^2}{\chi^2_{1-\alpha/2}(n-1)} \right] \]

使得概率为\(1-\alpha\)的区间理论上有无穷多个，它们有相同的置信度，本该选择其中精度最高（即长度最短）的，但是这样会很麻烦，为方便起见，选取\(\alpha/2\)分位数和\(1-\alpha/2\)分位数构造置信区间，这样的置信区间称为等尾置信区间。

4、\(\mu\)已知时\(\sigma^2\)的区间估计

看起来，\(S^2\)这个枢轴量不考虑\(\mu\)是否已知，但是枢轴量法是依赖于点估计的，自然我们首先会考虑的是充分统计量，而\(S^2\)在\(\mu\)已知时，不是\(\sigma^2\)的充分统计量。为此，我们要基于\(\sigma^2\)的充分统计量构建枢轴量。令

\[Q=\sum_{j=1}^n(X_j-\mu)^2, \]

它是\(\sigma^2\)的充分统计量，且我们可以将其转化为\(\chi^2\)分布：

\[\frac{Q}{\sigma^2}=\sum_{j=1}^n\left(\frac{X_j-\mu}{\sigma} \right)^2\sim \chi^2(n), \]

这是由于各个\(X_j\)相互独立服从\(N(\mu,\sigma^2)\)，于是可以构造出概率区间\(\frac{Q}{\sigma^2}\in[\chi^2_{1-\alpha/2}(n),\chi^2_{\alpha/2}(n)]\)，因此\(\sigma^2\)的置信区间是

\[\left[\frac{Q}{\chi^2_{\alpha/2}(n)},\frac{Q}{\chi^2_{1-\alpha/2}(n)} \right]. \]

Part 4：双正态总体参数区间估计

双总体\(X\sim N(\mu_1,\sigma_1^2)\)、\(Y\sim N(\mu_2,\sigma_2^2)\)的参数估计，主要指的是均值差和方差比，但是要分情况讨论，这是因为如果不加任何限制，它们的置信区间理论还不是很完善。

以下记\(X_1,\cdots,X_m\)是从\(X\)中抽取的样本，相应的样本均值和样本方差是\(\bar X\)和\(S_x^2\)；\(Y_1,\cdots,Y_n\)是从\(Y\)中抽取的样本，相应的样本均值和样本方差是\(\bar Y\)和\(S_y^2\)。

1、均值差\(\mu_2-\mu_1\)的区间估计

第一种情况是\(\sigma_1^2,\sigma_2^2\)未知但\(m=n\)时，即样本容量相等时。一种简单的做法是构造\(Z_j=Y_j-X_j\)，即让成对数据相减，这样\(Z_1,\cdots,Z_n\)便独立同分布于\(N(\mu_2-\mu_1,\sigma_1^2+\sigma_2^2)\)，相当于从单总体中抽样，并对总体均值作估计。显然，枢轴量应该是

\[\frac{\sqrt{n}[\bar Z-(\mu_2-\mu_1)]}{S_z}\sim t(n-1). \]

所以置信区间是

\[\left[\bar Z-\frac{S_z}{\sqrt{n}}t_{\alpha/2}(n-1),\bar Z+\frac{S_z}{\sqrt{n}}t_{\alpha/2}(n-1) \right]. \]

不过要注意的是，构造成对数据时，实际上丢失了部分信息，这是因为\(Z_1,\cdots,Z_n\)并非\(\mu_2-\mu_1\)的充分统计量。

总而言之，当\(m=n\)时，我们将其转化为成对数据，本质上还是单总体参数估计。

第二种情况是\(\sigma_1^2,\sigma_2^2\)已知时，此时用\(\bar Y-\bar X\)来最大程度地估计\(\mu_2-\mu_1\)，则有

\[\bar Y-\bar X\sim N\left(\mu_2-\mu_1,\frac{\sigma_1^2}{m}+\frac{\sigma_2^2}{n} \right), \]

于是枢轴量是

\[\frac{\bar Y-\bar X-(\mu_2-\mu_1)}{\sqrt{\frac{\sigma_1^2}{m}+\frac{\sigma_2^2}{n}}}\sim N(0,1), \]

\(\mu_2-\mu_1\)的置信区间为

\[\left[\bar Y-\bar X-u_{\alpha/2}\sqrt{\frac{\sigma_1^2}{m}+\frac{\sigma_2^2}{n}},\bar Y+\bar X+u_{\alpha/2}\sqrt{\frac{\sigma_1^2}{m}+\frac{\sigma_2^2}{n}} \right]. \]

第三种情况稍微复杂一些，也是最常处理的一种情况，即\(\sigma_1^2=\sigma_2^2=\sigma^2\)但未知时。此时仍有

\[\bar Y-\bar X\sim N\left(\mu_2-\mu_1,\sigma^2\sqrt{\frac{1}{m}+\frac{1}{n}} \right), \]

为了解决\(\sigma^2\)未知的问题，也要用适当的样本方差来替代，但此时如此构造：

\[Q=\sum_{j=1}^m(X_j-\bar X)^2+\sum_{j=1}^n(Y_j-\bar Y)^2, \]

可以发现

\[\frac{Q}{\sigma^2}=\sum_{j=1}^m\left(\frac{X_j-\bar X}{\sigma} \right)^2+\sum_{j=1}^n\left(\frac{Y_j-\bar Y}{\sigma} \right)^2\stackrel{d}=\chi^2(m-1)+\chi^2(n-1)\stackrel{d}=\chi^2(n+m-2). \]

于是用\(Q/(n+m-2)\)代替\(\sigma^2\)最合适不过了，因此

\[\frac{\frac{\bar Y-\bar X-(\mu_2-\mu_1)}{\sigma\sqrt{\frac{1}{m}+\frac{1}{n}}}}{\sqrt{\frac{Q}{\sigma^2}/(n+m-2)}}=\sqrt{\frac{mn(m+n-2)}{m+n}}\frac{(\bar Y-\bar X)-(\mu_2-\mu_1)}{\sqrt{Q}}\sim t^2(m+n-2), \]

即\(\mu_2-\mu_1\)的置信区间为

\[\left[(\bar Y-\bar X)-t_{\alpha/2}(n+m-2)\sqrt{\frac{Q(m+n)}{(m+n-2)mn}},(\bar Y-\bar X)+t_{\alpha/2}(n+m-2)\sqrt{\frac{Q(m+n)}{(m+n-2)mn}} \right]. \]

现进行模拟，每次实验中，从\(N(3,9)\)中抽取5个样本，从\(N(5,25)\)中抽取8个样本，对均值差进行估计。进行10000次重复试验。

rm(list = ls())
dev.off()

m <- 5
n <- 8
t <- qt(0.975, m+n-2)
upper.bound <- c()
lower.bound <- c()

for (j in 1:10000){
  xlst <- rnorm(m, 3, 3)
  ylst <- rnorm(n, 5, 5)
  My <- mean(ylst)
  Mx <- mean(xlst)
  Q <- (m-1)*var(xlst) + (n-1)*var(ylst)
  upper.bound[j] <- My-Mx+t*sqrt( (Q*(m+n)) / ((m+n-2)*m*n) )
  lower.bound[j] <- My-Mx-t*sqrt( (Q*(m+n)) / ((m+n-2)*m*n) )
}

plot(1:10000, rep(2,10000), xlab = "Experiment", ylab = "CI", main = "CI of the mean difference", cex=0.1, ylim = c(-13, 17))
points(1:10000, upper.bound, col = "red", cex = 0.1)
points(1:10000, lower.bound, col = "blue", cex = 0.1)
sum(upper.bound < 2 | lower.bound > 2)  # 输出结果为302

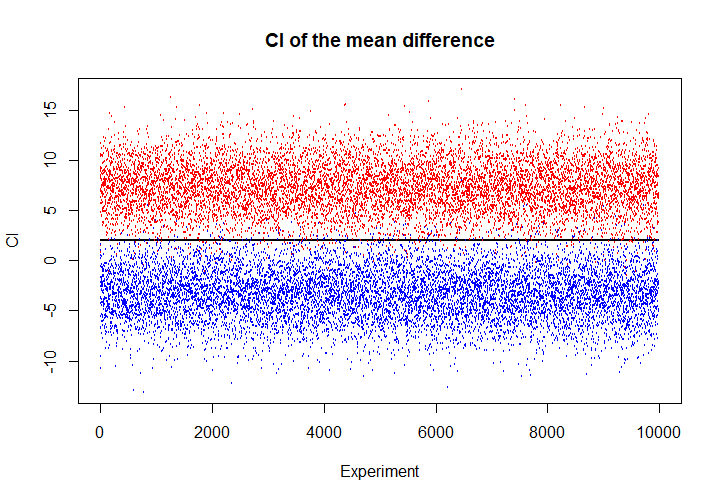
当我们将样本容量提升至\(m=200\)，\(n=100\)时，出现了929个不包含真值的区间。看起来区间估计是否包含真值，与\(m,n\)的相对大小有很大的关系。

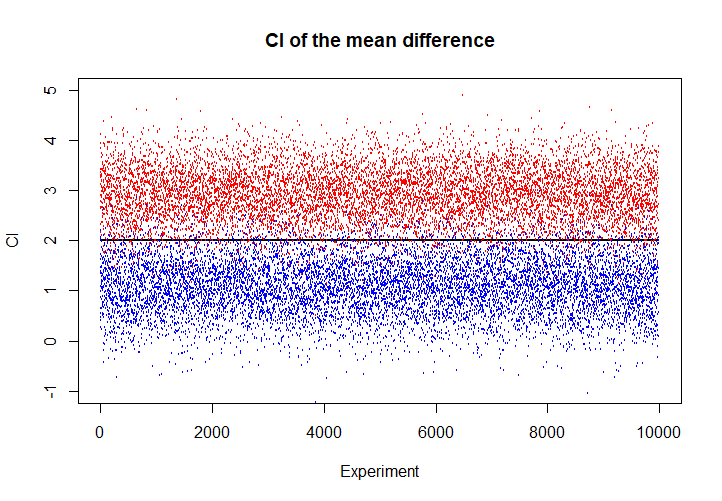
当\(\sigma_1^2\ne \sigma_2^2\)且未知时，均值差的参数估计称为Behrens-Fisher问题，比较复杂，这里不加讨论。

2、方差比\(\sigma_2^2/\sigma_1^2\)的区间估计

事实上方差比比较好讨论，因为方差的估计量一定是自己总体中所抽取的样本方差，故服从某个\(\chi^2\)分布，作比后应当能得到\(F\)分布，这里简要地讨论两种情况。

首先是\(\mu_1,\mu_2\)都未知的情况，此时自然\(S_x^2,S_y^2\)会被用作估计量，由于

\[\frac{(m-1)S_x^2}{\sigma_1^2}\sim \chi^2(m-1),\quad \frac{(n-1)S_y^2}{\sigma_2^2}\sim \chi^2(n-1), \]

所以

\[\frac{\frac{(m-1)S_x^2}{\sigma_1^2}/(m-1)}{\frac{(n-1)S_y^2}{\sigma_2^2}/(n-1)}=\frac{S_x^2}{S_y^2}\frac{\sigma_2^2}{\sigma_1^2}\sim F(m-1,n-1), \]

故应有\(\frac{S_x^2\cdot\sigma_2^2}{S_y^2\cdot\sigma_1^2}\in[F_{1-\alpha/2}(m-1,n-1),F_{\alpha/2}(m-1,n-1)]\)，所以置信区间为

\[\left[\frac{S_y^2}{S_x^2}F_{1-\alpha/2}(m-1,n-1),\frac{S_y^2}{S_x^2}F_{\alpha/2}(m-1,n-1) \right]. \]

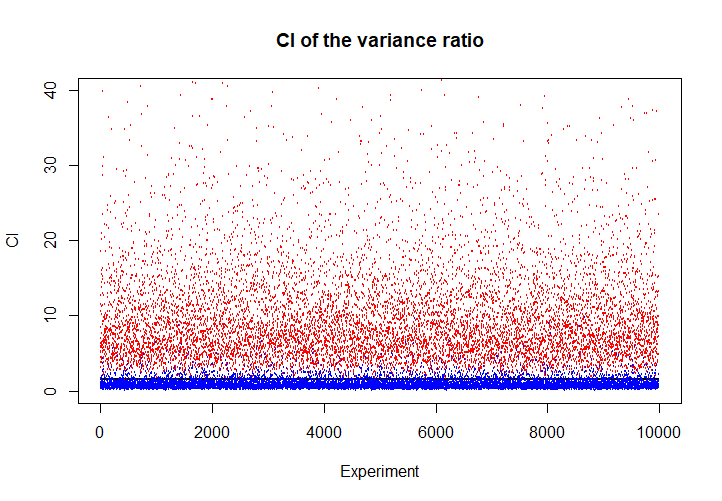
进行模拟，每次实验中，从\(N(3,9)\)中抽取9个样本，从\(N(5,25)\)中抽取25个样本，对方差比进行估计。进行10000次重复试验。

rm(list = ls())
dev.off()

m <- 9
n <- 25
f1 <- qf(0.025, m-1, n-1)
f2 <- qf(0.975, m-1, n-1)
upper.bound <- c()
lower.bound <- c()

for (j in 1:10000){
  xlst <- rnorm(m, 3, 3)
  ylst <- rnorm(n, 5, 5)
  Sx2 <- var(xlst)
  Sy2 <- var(ylst)
  lower.bound[j] <- Sy2/Sx2 * f1
  upper.bound[j] <- Sy2/Sx2 * f2
}

plot(1:10000, rep(25/16,10000), xlab = "Experiment", ylab = "CI", main = "CI of the variance ratio", cex=0.1, ylim = c(0, 40))
points(1:10000, upper.bound, col = "red", cex = 0.1)
points(1:10000, lower.bound, col = "blue", cex = 0.1)
sum(upper.bound < 25/16 | lower.bound > 25/16)

然后是\(\mu_1,\mu_2\)均已知的情况，这时方差的估计量会是

\[Q_x^2=\frac{1}{m}\sum_{j=1}^m(X_j-\mu_1)^2,\quad Q_y^2=\frac{1}{n}\sum_{j=1}^n(Y_j-\mu_2)^2, \]

显然有

\[\frac{mQ_x^2}{\sigma_1^2}\sim \chi^2(m),\quad \frac{nQ_y^2}{\sigma_2^2}\sim\chi^2(n), \]

于是枢轴量为

\[\frac{\frac{mQ_x^2}{\sigma_1^2}/m}{\frac{nQ_y^2}{\sigma_2^2}/n}=\frac{Q_x^2}{Q_y^2}\frac{\sigma_2^2}{\sigma_1^2}\sim F(m,n), \]

即\(\sigma_2^2/\sigma_1^2\)的区间估计为

\[\left[\frac{Q_y^2}{Q_x^2}F_{1-\alpha/2}(m,n),\frac{Q_y^2}{Q_x^2}F_{\alpha/2}(m,n) \right]. \]

事实上，方差的估计，就是在\(\mu\)已知时使用对均值的离差平方和，在\(\mu\)未知时使用对样本均值的离差平方和，注意分母与\(\chi^2\)分布的自由度即可。由此，读者应该也能推断出\(\mu_1\)已知\(\mu_2\)未知，或者\(\mu_1\)未知\(\mu_2\)已知时方差比的区间估计了。

---

本文给出了区间估计的求法——枢轴量法的实际应用案例，并对正态总体的参数作区间估计。下篇文章将着眼于非正态总体的区间估计，由于非正态总体不像正态总体一样，拥有性质良好、分布透明的点估计可以使用，所以我们可能需要寻找一种更通用的方法来求区间估计。