数理统计2：为什么是正态分布，正态分布均值与方差的估计，卡方分布

上一篇文章提到了一大堆的统计量，但是没有说到它们的用处。今天，我们就会接触到部分估计量，进入到数理统计的第一大范畴——参数估计，同时也会开始使用R语言进行模拟。由于本系列为我独自完成的，缺少审阅，如果有任何错误，欢迎在评论区中指出，谢谢！

目录

• Part 1：为什么是正态分布
• Part 2：正态分布均值估计
• Part 3：正态分布方差估计
• Part 4：卡方分布

Part 1：为什么是正态分布

为什么要突然提到正态分布的参数估计？原因有以下几个。首先，正态分布是生活中最常见的分布，许多随机事件的分布可以用正态分布来概括。林德贝格勒维中心极限定理告诉我们，二阶矩存在的独立同分布随机变量列\(\{\xi_n\}\)，记它们的和为\(S_n\)，\(\mathbb{E}(\xi_1)=\mu\)，\(\mathbb{D}(\xi_n)=\sigma^2\)，则

\[\frac{S_n-n\mu}{\sqrt{n}\sigma}\stackrel{d}\to N(0,1). \]

刚刚学完概率论的同学应该对这个结论不陌生。

而中心极限定理的条件实际上并不需要这么强，林德贝格费勒定理去除了同分布的约束，只要\(\{\xi_n\}\)满足\(\forall \tau>0\)，

\[\frac{1}{\sum_{k=1}^n\mathbb{D}(\xi_k)}\sum_{k=1}^n\int_{|x+\mathbb{E}(\xi_k)|\ge \tau\sqrt{\sum_{k=1}^n \mathbb{D}(\xi_k)}}(x-\mathbb{E}(\xi_k))^2\mathrm{d}F_k(x)\to 0, \]

就有

\[\frac{\sum_{k=1}^n(\xi_k-\mathbb{E}(\xi_k))}{\sqrt{\sum_{k=1}^n \mathbb{D}(\xi_k)}}\stackrel{d}\to N(0,1). \]

这说明自然界中微小随机项的累积效应普遍服从中心极限定理。

另外，正态分布的信息完全由两个参数所决定：期望和方差，即前两阶矩。因此，如果我们假定总体是服从正态分布的，就只需要对其两个参数作估计，这给问题的讨论带来方便。最后就是正态分布在实用上的意义了，两个独立正态分布的和、差甚至乘积都是正态分布，这在实用上也很方便，所以许多时候即使总体不服从正态分布，也近似认为服从正态分布。

Part 2：正态分布均值估计

既然正态分布完全由两个参数所决定，那么只要知道出这两个参数的值（或者范围），就能确定总体的全部信息。然而，在实际生活中要获得绝对正确的正态分布参数是不可能的，因为生活中的总体情况总是未知，要认识总体，我们只能从总体中抽取一系列样本，再通过样本性质来估计总体。

最简单的情况是简单随机抽样，这时候每一个样本都和总体具有相同的分布函数或密度函数。具体对于正态分布来说，\(X\sim N(\mu,\sigma^2)\)，如果我们抽取了\(n\)个简单随机样本\((X_1,X_2,\cdots,X_n)\)，则\(X_1,\cdots,X_n\)之间实际上相互独立，且\(\forall i,X_i\sim N(\mu,\sigma^2)\)。尽管\(\mu\)和\(\sigma^2\)我们未知，但是我们知道一点——它们一定是不会变化的常数，这样，我们能够获得独立且与总体分布相同的样本，通过观测样本构造统计量来估计总体。这种将统计量的观测值作为参数估计的估计方式，称为点估计。

对于总体均值，很自然的一点是用样本均值作为总体均值的估计。似乎没有理由不这么做，但这么做有什么依据吗？我们知道，观测样本具有两重性，所以统计量也具有两重性。要研究用样本均值作为总体均值估计的合理性，必须观察样本均值作为随机变量时的分布。

正态分布具有可加性，这指的是对于相互独立的正态分布，它们的和作为一个随机变量仍然服从正态分布，且均值和方差都是各分量的直接加和。有了这一点，我们就可以研究样本均值的分布了。

\[T_n\xlongequal{def}\sum_{j=1}^nX_j \\ \bar X=\frac{1}{n}\sum_{j=1}^n X_j=\frac{1}{n}T_n, \]

由于正态分布服从可加性，因此有

\[T_n\sim N(n\mu,n \sigma^2). \]

另外，由于正态分布的数乘依然是正态分布，且均值相当于乘上常数，方差相当于乘上常数的平方，所以

\[\bar X=\frac{1}{n}T_n\sim N\left(\mu,\frac{\sigma^2}{n}\right). \]

直观上来看，样本均值与总体具有相同的均值，但是方差变成了原来的\(n\)分之一。众所周知，方差代表随机变量取值的离散情况，由切比雪夫不等式有\(\forall\varepsilon>0\)，

\[\mathbb{P}(|\bar X-\mu|>\varepsilon)\le \frac{\mathbb{D}(\bar X)}{\varepsilon^2}=\frac{\sigma^2}{n\varepsilon^2}. \]

这个式子表明，只要你的\(n\)无限增大，\(\bar X\)和\(\mu\)之间的差距就可以无限缩小，这个性质称为弱相合性。另外，样本均值的期望和要估计的参数\(\mu\)一致，这个性质称为无偏性。由于样本均值估计总体均值时具有无偏性、弱相合性等优点，所以我们很难不把样本均值当作总体均值的点估计。

下面是用R语言从\(N(5,25)\)中获得100次样本均值的程序，每一个样本均值是由10000个相互独立的样本构成的。

rm(list = ls())  # 清空内存
barxlst <- c()
for (i in 1:100){
  barxlst[i] <- mean(rnorm(10000, 5, 5))
}
split.screen(c(1, 2))
screen(1)
plot(barxlst)  # 绘制散点图
screen(2)
hist(barxlst)  # 绘制直方图

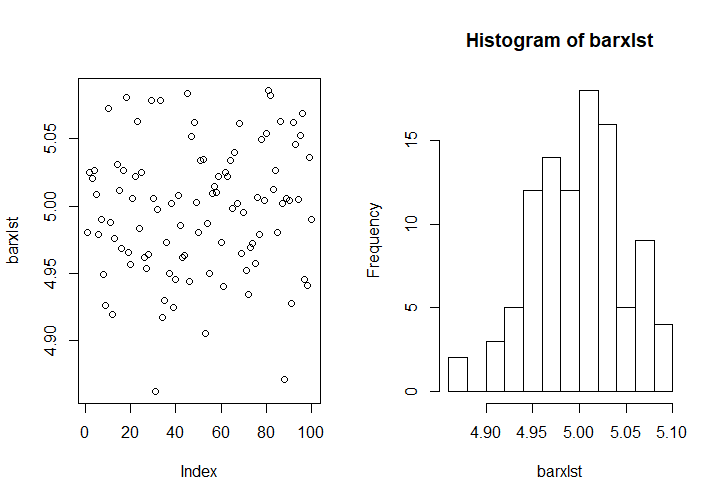
从图上可以看到，样本均值的集中区间几乎都在\(4.9\sim 5.1\)之间，读者可以自行利用正态分布的\(3\sigma\)性质验证这一点。

Part 3：正态分布方差估计

接下来就轮到第二个参数\(\sigma^2\)了，大家也很容易想到用样本方差

\[S^2=\frac{1}{n-1}\sum_{j=1}^n(X_j-\bar X)^2 \]

作为总体方差的估计，但随之而来的就有两个问题：

1. 为什么要用\(S^2\)这个估计量？
2. 为什么\(S^2\)的分母是\(n-1\)而不是\(n\)？

这里我们依然要探究\(S^2\)的分布，但在此之前，先探究一下\(S^2\)的均值，这比探究\(S^2\)的分布要更容易。为此，可以作如下的变形：

\[\begin{aligned} S^2&=\frac{1}{n-1}\sum_{j=1}^n(X_j-\bar X)^2\\ &=\frac{1}{n-1}\sum_{j=1}^n[X_j-\mu-(\bar X-\mu)]^2\\ &=\frac{1}{n-1}\left[\sum_{j=1}^n(X_j-\mu)^2+n(\bar X-\mu)^2-2\sum_{j=1}^n(X_j-\mu)(\bar X-\mu) \right]. \end{aligned} \]

对于每一个\(X_j\)，有\((X_j-\mu)\sim N(0,\sigma^2)\)，所以易得\(\mathbb{E}(X_j-\mu)^2=\sigma^2\)；由于\((\bar X-\mu)\sim N(0,\sigma^2/n)\)，所以\(\mathbb{E}(\bar X-\mu)^2=\sigma^2/n\)。最后一部分，有

\[\begin{aligned} &\quad \sum_{j=1}^n(X_j-\mu)(\bar X-\mu)\\ &=(\bar X-\mu)\left[\sum_{j=1}^nX_j-n\mu\right]\\ &=n(\bar X-\mu)^2, \end{aligned} \]

所以

\[\begin{aligned} \mathbb{E}(S^2)&=\frac{1}{n-1}\left[\sum_{j=1}^n\mathbb{E}(X_j-\mu)^2-n\mathbb{E}(\bar X-\mu)^2 \right]\\ &=\frac{n}{n-1}\sigma^2-\frac{n}{n-1}\cdot\frac{\sigma^2}{n}\\ &=\sigma^2. \end{aligned} \]

这说明\(S^2\)在估计\(\sigma^2\)上是无偏的，这样我们就解决了第二个问题：为什么\(S^2\)的分母是\(n-1\)而不是\(n\)，这是因为\(n-1\)作分母可以让统计量具有无偏性。

下面就是为什么要用\(S^2\)估计\(\sigma^2\)的问题，照理说具有无偏性的估计量可以有这么多，为什么选择了样本方差呢？回想总体均值的估计，事实上如果我们只想获得一个无偏估计，使用\(X_1\)就够了（显然有\(\mathbb{E}(X_1)=\mu\)），但用\(X_1\)估计不具有相合性，也就是说不管你样本容量多大，这个统计量都不向着真值的方向靠近，这显然不是我们想要的效果。使用\(S^2\)是否也具有一样的相合性，是我们需要验证的问题。

注意下面的证明步骤十分重要，请大家务必将它记下来。

对于样本\(X_1,\cdots,X_n\)，使用施密特正交化构造一个如下的正交阵（不会不知道什么叫正交阵了吧）：

\[A=\begin{bmatrix} \frac{1}{\sqrt{n}} & \frac{1}{\sqrt{n}} & \cdots & \frac{1}{\sqrt{n}} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix}, \]

这个正交阵是一定可以构造出来的，如果你觉得很玄，下面是一个构造方式：

\[A=\begin{bmatrix} \frac{1}{\sqrt{n}} & \frac{1}{\sqrt{n}} & \frac{1}{\sqrt{n}} & \dots & \frac{1}{\sqrt{n}} \\ \frac{1}{\sqrt{2\cdot 1}} & \frac{-1}{\sqrt{2\cdot 1}} & 0 & \cdots & 0 \\ \frac{1}{\sqrt{3\cdot 2}} & \frac{1}{\sqrt{3\cdot 2}} & \frac{-2}{\sqrt{3\cdot 2}} & \cdots & 0 \\ \vdots & \vdots & \vdots & & \vdots \\ \frac{1}{\sqrt{n(n-1)}} & \frac{1}{\sqrt{n(n-1)}} & \frac{1}{\sqrt{n(n-1)}} & \cdots & \frac{-(n-1)}{\sqrt{n(n-1)}} \end{bmatrix}. \]

令\(\boldsymbol{X}=(X_1,\cdots,X_n)'\)，

\[\boldsymbol{Y}=(Y_1,\cdots,Y_n)'\xlongequal{def}AX, \]

则

\[Y_1=\sum_{j=1}^n\frac{1}{\sqrt{n}}X_j=\sqrt{n}\bar X. \]

由正交变换保持向量长度不变，得到

\[X_1^2+\cdots+X_n^2=Y_1^2+\cdots+Y_n^2, \]

所以

\[(n-1)S^2=\sum_{j=1}^n(X_j-\bar X)^2=\sum_{j=1}^nX_j^2-n\bar X^2=\sum_{j=1}^n Y_j^2-Y_1^2=\sum_{j=2}^nY_j^2. \]

接下来要证明一个很神奇的结论：\(Y_2,\cdots,Y_n\)独立同分布于\(N(0,\sigma^2)\)。首先由正态分布的线性组合仍然是正态分布这一性质，知道\(Y_2,\cdots,Y_n\)都服从正态分布，而它们的均值，对\(i=2,\cdots,n\)，有

\[\mu_i=\sum_{j=1}^na_{ij}\mathbb{E}(X_j)=\sum_{j=1}^na_{ij}\mu=\sqrt{n}\mu\sum_{j=1}^n a_{ij}\frac{1}{\sqrt{n}}=\sqrt{n}\mu\sum_{j=1}^n a_{ij}a_{1j}=0. \]

这里用到了正交矩阵第\(j\)行和第\(1\)行的正交性。它们的方差，对\(i=2,\cdots,n\)，有

\[\sigma_i^2=\sum_{j=1}^na_{ij}^2\mathbb{D}(X_j)=\sigma^2\sum_{j=1}^na_{ij}^2=\sigma^2, \]

这里用到了正交矩阵每一行平方和为1的性质。接下来还要证明\(\forall j\ne k\)，\(Y_jY_k\)相互独立（对于正态分布，即不相关），有

\[\mathrm{Cov}(Y_j,Y_k)=\sum_{i=1}^n a_{ij}a_{ik}\sigma^2=\sigma^2\sum_{i=1}^na_{ij}a_{ik}=0. \]

这就说明\(Y_1,Y_2,\cdots,Y_n\)相互独立，且\(Y_2,\cdots,Y_n\)独立同分布于\(N(0,\sigma^2)\)，所以它们的平方和为

\[(n-1)S^2=\sum_{j=2}^nY_j^2,\\ S^2=\frac{1}{n-1}\sum_{j=2}^n Y_j^2 \]

这里

\[\mathbb{E}(Y_j^2)=\sigma^2,\quad \mathbb{D}(Y_j^2)=\mathbb{E}(X_j^4)-\sigma^4=2\sigma^4,\\ \begin{aligned} \mathbb{E}(X_j^4)&=\int_{-\infty}^\infty x^4\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{x^2}{2\sigma^2}}\mathrm{d}x\\ &=\frac{1}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^\infty x^4\frac{-x}{\sigma^2}\frac{\sigma^2}{-x}\exp\left(-\frac{x^2}{2\sigma^2} \right)\mathrm{d}x\\ &=\frac{1}{\sqrt{2\pi\sigma^2}}(-\sigma^2)\int_{-\infty}^\infty x^3\mathrm{d}(e^{-\frac{x^2}{2\sigma^2}})\\ &=-\frac{\sigma}{\sqrt{2\pi}}\left(x^3e^{-\frac{x^2}{2\sigma^2}}\bigg|_{-\infty}^\infty -\int_{-\infty}^{\infty}3x^2e^{-\frac{x^2}{2\sigma^2}}\mathrm{d}x \right)\\ &=\frac{3\sigma^2}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^{\infty}x^2e^{-\frac{x^2}{2\sigma^2}}\mathrm{d}x\\ &=3\sigma^2\mathbb{E}(X_j^2)\\ &=3\sigma^4. \end{aligned} \]

所以

\[\mathbb{D}(S^2)=\frac{1}{n-1}\cdot\mathbb{D}(Y_1^2)=\frac{2\sigma^4}{n-1}, \\ \mathbb{P}(|S^2-\sigma^2|>\varepsilon)\le \frac{\mathbb{D}(S^2)}{\varepsilon^2}=\frac{2\sigma^4}{(n-1)\varepsilon^2}. \]

这就证明了\(S^2\)估计\(\sigma^2\)的弱相合性。同时，由于\(\bar X\)只是\(Y_1\)的函数，\(S^2\)只是\(Y_2,\cdots,Y_n\)的函数，由\(Y_1\)与\(Y_2,\cdots,Y_n\)的相互独立性，我们还能得到一个重要结论：\(\bar X\)与\(S^2\)相互独立。

以上的论证说明，\(\bar X\)作为\(\mu\)的估计是无偏且相合的，\(S^2\)作为\(\sigma^2\)的估计是无偏且相合的，并且\(\bar X\)与\(S^2\)相互独立。

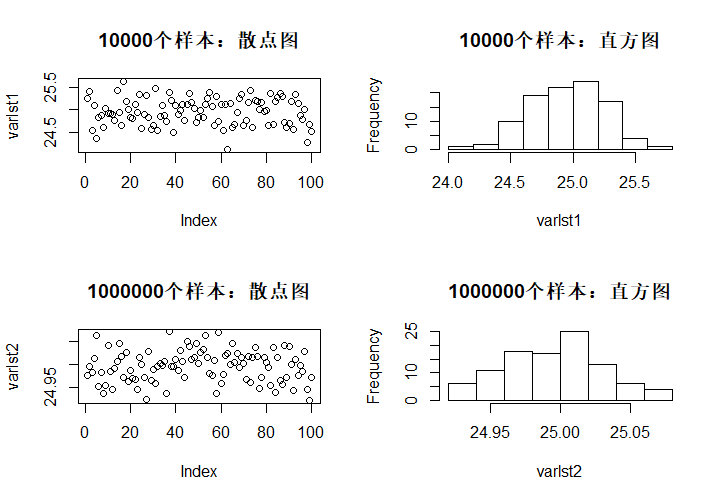
R语言中，var()函数能获得样本方差，对\(N(5,25)\)的10000个样本、1000000个样本进行100次模拟，注意观察坐标轴。

rm(list = ls())
varlst1 <- c()
varlst2 <- c()
for (i in 1:100){
  varlst1[i] <- var(rnorm(10000, 5, 5))
  varlst2[i] <- var(rnorm(1000000, 5, 5))
}

split.screen(c(2, 2))

screen(1)
plot(varlst1)
title("10000个样本：散点图")

screen(2)
hist(varlst1, main = "10000个样本：直方图")

screen(3)
plot(varlst2)
title("1000000个样本：散点图")

screen(4)
hist(varlst2, main = "1000000个样本：直方图")
# dev.off()

Part 4：卡方分布

以上对探索\(S^2\)的分布终究只是从它的一阶矩、二阶矩上证明了它用于刻画\(\sigma^2\)的优良性质，有没有办法能够得到\(S^2\)分布的详细信息呢？我们来观察\(S^2\)的表达式，注意到

\[(n-1)S^2=\sum_{j=2}^n Y_j^2=\sigma^2\sum_{j=2}^n\left(\frac{Y_j}{\sigma} \right)^2,\\ \frac{(n-1)S^2}{\sigma^2}=\sum_{j=2}^n\left(\frac{Y_j}{\sigma} \right)^2. \]

这样变换的意义在于，右边变成了\(n-1\)个独立同分布的标准正态随机变量的平方和，在数理统计中，我们会经常遇到类似于这样的分布，因此将其定义为卡方分布。以后我们会了解到，正态分布有三大常用的衍生分布，今天只介绍第一种。

定义：设\(X_1,\cdots,X_n\)独立同分布于\(N(0,1)\)，则称

\[\xi=\sum_{j=1}^n X_j^2\sim \chi^2(n). \]

这里\(n\)称为\(\chi^2\)分布的自由度。

从我们刚才对\(S^2\)的讨论，容易知道如果\(\xi\sim \chi^2(n)\)，则

\[\mathbb{E}(\xi)=n,\quad \mathbb{D}(\xi)=2n. \]

进一步，我们还可以求出\(\xi\)的密度函数为

\[f_\xi(x)=\frac{1}{2^{\frac{n}2}\Gamma(\frac{n}{2})}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}I_{(x>0)}. \]

这里\(I_A\)是示性函数，即\(A\)发生时取1不发生时取0。在数理统计中，选择示性函数而不是分段函数的形式表示密度函数会给问题的讨论带来极大的方便。目前，记忆卡方分布的密度还挺有难度的，但我们可以暂且跳过它。

由于\(X_1,\cdots,X_n\)独立同分布服从于\(N(0,1)\)，所以其联合密度是

\[f(x_1,\cdots,x_n)=\left(\frac{1}{\sqrt{2\pi}} \right)^n\exp\left\{-\frac{1}{2}\sum_{j=1}^nx_j^2 \right\}, \]

设\(\xi=\sum_{j=1}^n X_j^2\)的分布函数为\(F_n(x)\)，则

\[F_n(x)=\left(\frac{1}{\sqrt{2\pi}} \right)^2\int\cdots\int_{\sum_{j=1}^nx_j^2<x}\exp\left\{-\frac{1}{2}\sum_{j=1}^nx_j^2 \right\}\mathrm{d}x_1\cdots\mathrm{d}x_n, \]

作以下球坐标变换：

\[\left\{\begin{array}l x_1=\rho\cos(\theta_1)\cos(\theta_2)\cdots\cos(\theta_{n-2})\cos(\theta_{n-1}), \\ x_2=\rho\cos(\theta_1)\cos(\theta_2)\cdots\cos(\theta_{n-2})\sin(\theta_{n-1}), \\ \vdots \\ x_n=\rho\sin(\theta_1), \end{array}\right. \]

该变换的Jacobi行列式绝对值为

\[|J|=\left|\frac{\partial(x_1,x_2,\cdots,x_n)}{\partial(\rho,\theta_1,\cdots,\theta_{n-1})} \right|=\rho^{n-1}g(\boldsymbol{\theta}). \]

这里\(\rho\le \sqrt{x}\)，\(g(\boldsymbol{\theta})\)是某个关于\(\boldsymbol{\theta}=(\theta_1,\cdots,\theta_{n-1})\)的函数，所以

\[\begin{aligned} F_n(x)&=\left(\frac{1}{\sqrt{2\pi}} \right)^2\int_{0}^{\sqrt{x}}\rho^{n-1}e^{-\frac{\rho^2}{2}}\mathrm{d}\rho\cdot\int_{\Theta} g(\boldsymbol{\theta})\mathrm{d}\boldsymbol{\theta}\\ &=C\int_{0}^{\sqrt{x}}\rho^{n-1}e^{-\frac{\rho^2} {2}}\mathrm{d}\rho\\ &\xlongequal{t:=\rho^2}C\int_{0}^{x}t^{\frac{n}{2}-1}e^{-\frac{t}{2}}\mathrm{d}t. \end{aligned} \]

这里\(C\)是某个常数，后面的部分为关于\(t\)的核，故显然\(\xi\)的密度为

\[f_n(x)=Cx^{\frac{n}{2}-1}e^{-\frac{x}{2}}I_{x>0}, \]

后面的部分称为密度函数的核，只要确定常数\(C\)即可，经过积分得到

\[C=\frac{1}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}. \]

最后指出\(\chi^2\)具有可加性，这指的是对于独立的\(X\sim \chi^2(n_1)\)，\(Y\sim \chi^2(n_2)\)，有

\[X+Y\sim \chi^2(n_1+n_2), \]

只要把\(X\)看成\(n_1\)个独立标准正态变量的平方和，\(Y\)看成\(n_2\)个独立标准正态变量的平方和，它们的和就是\(n_1+n_2\)个独立标准正态变量的平方和，故服从\(\chi^2(n_1+n_2)\)。

结合卡方分布，我们可以对今天得出的结论作一个小小的总结了。设\(X\sim N(\mu,\sigma^2)\)中抽取的简单随机样本导出的样本均值为\(\bar X\)，样本方差为\(S^2\)，则

1. \(\bar X\)的分布：

   \[\bar X\sim N\left(\mu,\frac{\sigma^2}{n} \right). \]

2. \(S^2\)的分布：

   \[\frac{(n-1)S^2}{\sigma^2}\sim \chi^2(n-1). \]

3. \(\bar X\)与\(S^2\)相互独立。

---

最后，有一个问题需要大家思考：正态参数的总体均值\(\mu\)和总体方差\(\sigma^2\)的无偏、相合估计量只有\(\bar X\)和\(S^2\)吗？如果不是，为什么我们会选择\(\bar X\)和\(S^2\)来估计总体参数呢？举个最简单的例子，如果我们取出了\(n\)个样本，那么用前\(n/2\)个（如果\(n\)是偶数）样本来计算样本均值和样本方差，一样是相合且无偏的。问题在于，为什么要用全部\(n\)个样本来计算，而不是只用部分的样本。

之后，我们会对更多的分布族讨论参数估计问题。