对课后习题的一些整理,由于不知道多元统计分析考试的内容,只能随便整理一些。如果有错误,请在评论区中指出。
第一题:条件分布与独立性
条件分布与独立性 一、设\(X\sim N_3(\mu,\Sigma)\),其中
\[\mu=\begin{bmatrix}
\mu_1 \\ \mu_2 \\ \mu_3
\end{bmatrix},\Sigma=\begin{bmatrix}
1 & \rho & \rho \\ \rho & 1 & \rho \\ \rho & \rho & 1
\end{bmatrix}.
\]
(1)求条件分布\((X_1,X_2|X_3)\);(2)给定\(X_3=x_3\)时,写出\(X_1,X_2\)的条件协方差。
解:(1)多元正态分布的条件分布依然是正态分布,所以\((X_1,X_2|X_3)\sim N_2(\mu_{12\cdot 3},\Sigma_{12\cdot 3})\),这里
\[\mu_{12\cdot 3}=\begin{bmatrix}
\mu_1 \\ \mu_2
\end{bmatrix}+\begin{bmatrix}
\rho \\ \rho
\end{bmatrix}(X_3-\mu_3)=\begin{bmatrix}
\mu_1+\rho(X_3-\mu_3) \\ \mu_2+\rho(X_3-\mu_3)
\end{bmatrix},\\
\Sigma_{12\cdot 3}=\begin{bmatrix}
1 & \rho \\ \rho & 1
\end{bmatrix}-\begin{bmatrix}
\rho^2 & \rho^2 \\ \rho^2 & \rho^2
\end{bmatrix}=\begin{bmatrix}
1-\rho^2 & \rho-\rho^2 \\ \rho-\rho^2 & 1-\rho^2
\end{bmatrix}.
\]
(2)由其条件分布得,
\[{\rm Cov}(X_1,X_2|X_3)=\rho-\rho^2.
\]
第二题:正态分布
正态分布的线性组合 二、设\(X\sim N_3(\mu,\Sigma)\),这里\(X=(X_1,X_2,X_3)'\),\(\mu=(2,-3,1)'\),
\[\Sigma=\begin{bmatrix}
1 & 1 & 1 \\ 1 & 3 & 2 \\ 1& 2 & 2
\end{bmatrix}.
\]
(1)求\(3X_1-2X_2+X_3\)的分布;(2)求\(a=(a_1,a_2)'\)使得\(X_3\)与\((X_1,X_2)'-aX_3\)相互独立。(3)已知\(X_2,X_3\)的观测值分别为\(x_2,x_3\),求\(X_1\)的最佳线性预测。
解:(1)设\(c=(3,-2,1)'\),则
\[c'X\sim N(c'\mu,c'\Sigma c),
\]
代入得到\(3X_1-2X_2+X_3\sim N(13,9)\)。
(2)这里
\[a=\begin{bmatrix}
1 \\ 2
\end{bmatrix}2^{-1}=\begin{bmatrix}
\frac{1}{2} \\ 1
\end{bmatrix}.
\]
(3)最佳线性预测即\(\mu_{1\cdot 23}\),而
\[\mu_{1\cdot 23}=\mu_1+\Sigma_{1,23}\Sigma_{23}^{-1}\begin{bmatrix}
x_2-\mu_2 \\ x_3-\mu_3
\end{bmatrix}=\frac{1}{2}x_3+\frac{1}{2}.
\]
第三题:均值检验
均值的似然比检验 三、设单个\(p\)元总体\(N_p(\mu,\Sigma)\)的均值向量检验问题,使用似然比原理导出检验\(H_0:\mu=\mu_0\)的似然比统计量以及分布,设\(\Sigma=\Sigma_0\)已知。
解:似然函数为
\[L(\mu)=\frac{1}{(2\pi)^{np/2}|\Sigma_0|^{n/2}}\exp\left(-\frac{1}{2}\sum_{i=1}^n(x_i-\mu)'\Sigma^{-1}_0(x_i-\mu) \right),
\]
故似然比统计量为
\[\begin{aligned}
\lambda=& \frac{L(\mu_0)}{L(\bar X)} \\
=& \exp\left\{\frac{1}{2}\sum_{i=1}^n[(x_i-\bar X)'\Sigma_0^{-1}(x_i-\bar X)-(x_i-\mu_0)'\Sigma_0^{-1}(x_i-\mu_0) ]\right\}\\
=&\exp\left\{-n\bar X'\Sigma_0^{-1}(\bar X-\mu_0)+\frac{n}{2}(\bar X-\mu_0)'\Sigma_{0}^{-1}(\bar X-\mu_0) \right\}\\
=&\exp\left\{-\frac{n}{2}(\bar X-\mu_0)'\Sigma_0^{-1}(\bar X-\mu_0) \right\}.
\end{aligned}
\]
也就是
\[-2\ln \lambda=(\bar X-\mu_0)'\left(\frac{\Sigma_0}{n}\right)^{-1}(\bar X-\mu_0).
\]
由于
\[\bar X-\mu_0\sim N_p\left(0,\frac{\Sigma_0}{n}\right).
\]
由多元正态分布的二次型分布,得到\(-2\ln \lambda\sim \chi^2(p)\)。
第四题:均值结构检验
均值向量分量检验 四、设\(X\sim N_p(\mu,\Sigma)\),这里\(\Sigma>0\)未知,记\(\mu=(\mu_1,\cdots,\mu_p)\),\(C\)为\(k\times p\)常数矩阵且\({\rm rank}(C)=k\),给出检验\(H_0:C\mu=r\)的检验统计量与分布。
解:\(CX\sim N_p(C\mu,C\Sigma C')\),即转化为均值向量未知时的假设检验。由于
\[\bar X\sim N_p\left(\mu,\frac{\Sigma}{n}\right),\quad A\sim W_p(n-1,\Sigma),
\]
所以
\[\sqrt{n}C(\bar X-\mu)\sim N_k(0,C\Sigma C'),\quad CAC'\sim W_k(n-1,C\Sigma C'),
\]
构造
\[T^2\xlongequal{def}n(C\bar X-r)'\left(\frac{CAC'}{n-1} \right)^{-1}(C\bar X-r)\sim T^2(k,n-1).
\]
即可利用\(T^2\)分布构造检验统计量。
本题给出的结论,可以研究均值内部结构的检验。
第五题:均值结构检验实例
均值的结构检验 五、假定某总体的三个变量\((X_1,X_2,X_3)\)有这样的规律:\(X_1:X_2:X_3=6:4:1\)。从总体\(X\)中抽取出\(6\)个样本,算得
\[\bar X=\begin{bmatrix}
82.0 \\ 60.2 \\ 14.5
\end{bmatrix},\quad A=\begin{bmatrix}
158.0 & 40.2 & 2.5 \\
40.2 & 15.86 & 6.55 \\
2.5 & 6.55 & 9.5
\end{bmatrix},
\]
检验这个规律是否真的存在。
解:定义结构矩阵为
\[C\xlongequal{def}\begin{bmatrix}
-1 & 0 & 6 \\
0 & -1 & 4
\end{bmatrix},
\]
则\(H_0:C\mu=0\),按照上题的方式构造检验统计量为
\[T_0^2=6(C\bar X)'\left(\frac{CAC}{5} \right)^{-1}(C\bar X)=47.1434,
\]
如果\(H_0\)成立,则\(T^2\sim T^2(2,5)\),结合\(F\)统计量与\(T\)统计量的关系,有
\[F=\frac{2}{5}T^2\sim F(2,4),F_0=18.857.
\]
查\(F\)分布表得到\(F_{0.01}=18\),所以\(F_0>F_{0.01}\),应当拒绝原假设,认为这个规律不存在。
第六题:协方差阵检验
协方差的似然比检验:六、对单个正态总体\(N_p(\mu,\Sigma)\),使用似然比检验导出\(H_0:\Sigma=\Sigma_0\)的似然比统计量及其分布,这里\(\mu\)未知。
解:似然比统计量为
\[\begin{aligned}
\lambda=&\frac{L(\bar X,\Sigma_0)}{L(\bar X,\frac{A}{n})}\\
=&\left(\frac{|\frac{A}{n}|}{|\Sigma_0|}\right)^{n/2}\exp\left(-\frac{1}{2}\sum_{i=1}^n[(x_i-\bar X)'\Sigma_0^{-1}(x_i-\bar X)-(x_i-\bar X)'(\frac{A}{n})^{-1}(x_i-\bar X)] \right)\\
=&\left(\frac{|\frac{A}{n}|}{|\Sigma_0|} \right)^{n/2}{\rm etr}\left[-\frac{1}{2}\left(\Sigma^{-1}_0-(\frac{A}{n})^{-1} \right)A \right]\\
=&\left(\frac{|\frac{A}{n}|}{|\Sigma_0|} \right)^{n/2}{\rm etr}\left(-\frac{1}{2}\Sigma_0^{-1}A+nI_p \right)\\
=&\left(\frac{e}{n} \right)^{np/2}|\Sigma_0^{-1}A|^{n/2}{\rm etr}\left(-\frac{1}{2}\Sigma_0^{-1}A \right).
\end{aligned}
\]
由Wilks定理,能够导出似然比统计量的极限分布为
\[-2\ln \lambda\stackrel {d}\to \chi^2\left(\frac{p(p+1)}{2} \right).
\]
第七题:距离判别
线性判别函数 七、考虑两个数据集:
\[X_1=\begin{bmatrix}
3 & 7 \\ 2 & 4 \\ 4 & 7
\end{bmatrix},X_2=\begin{bmatrix}
6 & 9 \\ 5 & 7 \\ 4 & 8
\end{bmatrix},
\]
计算线性判别函数,并给出训练集上的判断准确率。
解:计算两个数据集的数字特征,为
\[\bar X_1=\begin{bmatrix}
3 \\ 6
\end{bmatrix},\quad \bar X_2=\begin{bmatrix}
5 \\ 8
\end{bmatrix},\quad S_{\text{pooled}}=\begin{bmatrix}
1 & 1 \\ 1 & 2
\end{bmatrix},
\]
计算线性判别函数为
\[W(x)=(x-\frac{1}{2}(\bar X_1+\bar X_2))'S^{-1}(\bar X_1-\bar X_2)=8-2x_1, \\
x\in:\left\{\begin{array}l
X_1,& \text{if }W(x)>0; \\
X_2,& \text{if }W(x)\le 0.
\end{array}\right.
\]
在此线性判别函数下,\(X_1\)的三个样本中两个判断正确,一个判断错误,\(X_2\)的三个样本全部判断正确。
第八题:贝叶斯判别
贝叶斯判别 八、设有两个二元正态总体\(G_1,G_2\),相关数字特征如下:
\[\mu_{(1)}=\begin{bmatrix}
10 \\ 15
\end{bmatrix},\mu_{(2)}=\begin{bmatrix}
20 \\ 25
\end{bmatrix},\\
\Sigma_{\text{pooled}}=\begin{bmatrix}
18 & 12 \\ 12 & 32
\end{bmatrix}.
\]
如果先验概率\(q_1=q_2\),错判损失为\(L(2|1)=10\),\(L(1|2)=75\),则以下两个样品应当如何归类?
\[X_{(1)}=\begin{bmatrix}
20 \\ 20
\end{bmatrix},X_{(2)}=\begin{bmatrix}
15 \\ 20
\end{bmatrix}.
\]
解:贝叶斯判别使得平均损失最小,将样本\(X\)判定给\(G_1\)和\(G_2\)的损失分别是
\[h_1(X)=q_2f_2(X)L(1|2)=75q_2f_2(X),\\
h_2(X)=q_1f_1(X)L(2|1)=10q_1f_1(X).
\]
分别取其对数,有
\[\ln h_1(X)=C-\frac{1}{2}(X-\mu_{(2)})'\Sigma_{\text{pooled}}^{-1}(X-\mu_{(2)})+\ln75,\\
\ln h_2(X)=C-\frac{1}{2}(X-\mu_{(1)})'\Sigma_{\text{pooled}}^{-1}(X-\mu_{(1)})+\ln10.
\]
计算得
\[h_1(X_{(1)})=C+\ln(75)-\frac{25}{48},\quad h_2(X_{(1)})=C+\ln(10)-\frac{1225}{432}.
\]
因为\(h_1(X_{(1)})>h_2(X_{(1)})\),所以应该把\(X_{(1)}\)归为\(G_2\)。或者直接计算
\[\frac{h_2(X)}{h_1(X)}=\frac{10f_1(X)}{75f_2(X)}=\frac{2}{25}\exp\left\{(\mu_{(1)}-\mu_{(2)})'\Sigma_{\text{pooled}}^{-1}\left[X-\frac{1}{2}(\mu_{(1)}+\mu_{(2)}) \right] \right\}.
\]
将\(X_{(2)}\)代入计算,得到
\[\frac{h_2(X_{(2)})}{h_1(X_{(1)})}=\frac{2}{25}<1,\quad h_2(X_{(2)})<h_{1}(X_{(2)}),
\]
所以应该把\(X_{(2)}\)判为\(G_2\)。
第九题:费希尔判别
费希尔判别 九、设有两个二元正态总体\(G_1,G_2\),相关数字特征如下:
\[\mu_{(1)}=\begin{bmatrix}
10 \\ 15
\end{bmatrix},\mu_{(2)}=\begin{bmatrix}
20 \\ 25
\end{bmatrix},\\
\Sigma_1=\begin{bmatrix}
18 & 12 \\ 12 & 32
\end{bmatrix},\Sigma_2=\begin{bmatrix}
20 & -7 \\ -7 & 5
\end{bmatrix}.
\]
使用Fisher判别法,对以下两个样品归类:
\[X_{(1)}=\begin{bmatrix}
20 \\ 20
\end{bmatrix},X_{(2)}=\begin{bmatrix}
15 \\ 20
\end{bmatrix}.
\]
解:由于此时没有样本,我们就取\(\bar \mu=\frac{1}{2}(\mu_{(1)}+\mu_{(2)})\),
\[A=\Sigma_1+\Sigma_2=\begin{bmatrix}
38 & 5 \\ 5 & 37
\end{bmatrix},\\
B=(\mu_{(1)}-\bar\mu)'(\mu_{(1)}-\bar \mu)+(\mu_{(2)}-\bar \mu)'(\mu_{(2)}-\bar \mu)=\begin{bmatrix}
50 & 50 \\ 50 & 50
\end{bmatrix}.
\]
所以
\[A^{-1}B=\frac{1}{d}\begin{bmatrix}
32 & 32 \\ 33 & 33
\end{bmatrix},
\]
其最大特征值对应的特征向量为\(a=(32,33)'\)。设\(\nu_{(1)}=a'\mu_{(1)}\),\(\nu_{(2)}=a'\mu_{(2)}\),\(\sigma_1=a'\Sigma_1a\),\(\sigma_2=a'\Sigma_2a\),\(u_{(1)}=a'X_{(1)}\),\(u_{(2)}=a'X_{(2)}\),则
\[\nu_{(1)}=815,\quad \nu_{(2)}=1465,\\
\sigma_1=78624,\quad \sigma_2=11141;\\
u_{(1)}=1300,\quad u_{(2)}=1140.
\]
计算其马氏距离,有
\[d_1(u_{(1)})=\frac{|1300-815|}{\sqrt{78624}}=1.730,\\
d_2(u_{(1)})=\frac{|1300-1465|}{\sqrt{11141}}=1.563;\\
d_1(u_{(2)})=\frac{|1140-815|}{\sqrt{78624}}=1.159;\\
d_2(u_{(2)})=\frac{|1140-1465|}{\sqrt{11141}}=-3.079.
\]
所以\(u_{(1)}\)应该归为\(G_2\),\(u_{(2)}\)都应该归为\(G_1\)。
第十题:类平均法聚类
系统聚类 十、用类平均法作系统聚类,距离阵如下。
\[D^{(0)}=\begin{bmatrix}
0 & \\
4 & 0 \\
6 & 9 & 0 \\
1 & 7 & 10 & 0 \\
6 & 3 & 5 & 8 & 0
\end{bmatrix}.
\]
解:类平均法的距离递推公式为
\[D_{rk}^2=\frac{n_p}{n_r}D^2_{pk}+\frac{n_q}{n_r}D_{qk}^2.
\]
第一次聚类,将样本1和4归为一类,记作\(CL_1=(1,4)\),第一层高度为1。
\[d^2(CL_1,2)=\frac{1}{2}(16+49)=32.5,\\
d^2(CL_1,3)=\frac{1}{2}(36+100)=68,\\
d^2(CL_1,5)=\frac{1}{2}(36+64)=50.
\]
此时的距离矩阵(平方)为
\[D^2_{(1)}=\begin{matrix}
CL_1 \\ 2 \\ 3 \\ 5
\end{matrix}\begin{bmatrix}
0 \\
32.5 & 0 \\
68 & 81 & 0\\
50 & 9 & 25 & 0
\end{bmatrix}.
\]
第二次聚类,将样品2和5归为一类,记作\(CL_2=(2,5)\),第二层高度为3。
\[d^2(CL_2,CL_1)=\frac{1}{2}(32.5+50)=41.25,\\
d^2(CL_2,3)=\frac{1}{2}(81+25)=53,\\
\]
此时的距离矩阵(平方)为
\[D_{(2)}^{2}=\begin{matrix}
CL_1 \\ CL_2 \\ 3
\end{matrix}\begin{bmatrix}
0 \\
41.25 & 0 \\
68 & 53 & 0
\end{bmatrix}.
\]
第三次聚类,将CL1和CL2归为一类,记作\(CL_3=(1,4,2,5)\),第三层高度为\(\sqrt{41.25}\)。
\[d^2(CL_3,3)=\frac{1}{2}(68+53)=60.5.
\]
此时的距离矩阵(平方)为
\[D_{(3)}^2=\begin{matrix}
CL_3 \\ 3
\end{matrix}\begin{bmatrix}
0 \\ 60.5 & 0
\end{bmatrix}
\]
第四次聚类,将所有样本归为一类,第四层高度为\(\sqrt{60.5}\)。谱系聚类图为
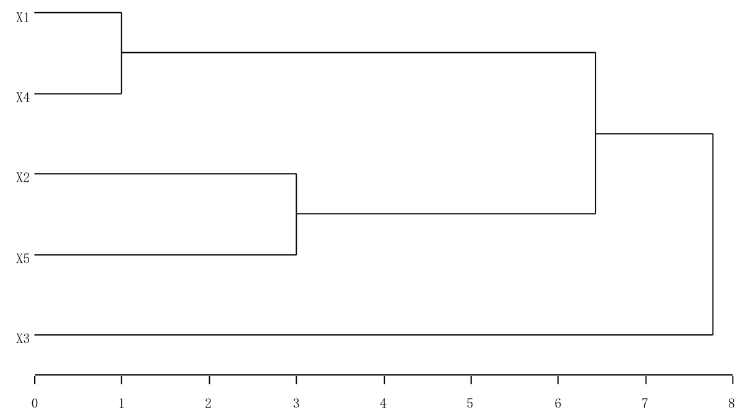
第十一题:主成分分析
主成分分析 十一、设随机向量\(X\)的协方差阵是
\[\Sigma=\begin{bmatrix}
4 & 3 & 2 & 1 \\
3 & 4 & 1 & 2 \\
2 & 1 & 4 & 3 \\
1 & 2 & 3 & 4
\end{bmatrix},
\]
试求\(X\)的主成分,在0.7的总体贡献率要求下,求需要的主成分个数,并求出这些主成分对\(X_2\)的贡献率。
解:求\(\Sigma\)的特征值有
\[\lambda_1=10,\lambda_2=4,\lambda_3=2,\lambda_4=0,
\]
所以只需要取2个主成分即可,对应的单位特征向量为
\[a_1=\frac{1}{2}(1,1,1,1)',\quad a_2=\frac{1}{2}(1,1,-1,-1)'.
\]
所以主成分为
\[Z_1=\frac{1}{2}(X_1+X_2+X_3+X_4),\\
Z_2=\frac{1}{2}(X_1+X_2-X_3-X_4).
\]
有
\[\rho(Z_1,X_2)=\frac{{\rm Cov}(Z_1,X_2)}{\sqrt{\mathbb{D}(Z_1)\mathbb{D}(X_2)}}=\frac{5}{\sqrt{10\cdot 4}}=\frac{\sqrt{10}}{4},\\
\rho(Z_2,X_2)=\frac{{\rm Cov}(Z_2,X_2)}{\sqrt{\mathbb{D}(Z_2)\mathbb{D}(X_2)}}=\frac{1}{2}.
\]
这里也可以利用
\[\rho(Z_1,X_2)=\frac{\sqrt{\lambda_1}a_1'e_2}{\sqrt{\mathbb{D}(X_2)}}=\frac{\sqrt{10}}{4}
\]
来算,更快。
所以前2个主成分对\(X_2\)的贡献为
\[\nu_2^{(2)}=\rho^2(Z_1,X_2)+\rho^2(Z_2,X_2)=\frac{7}{8}.
\]
第十二题:因子模型
因子模型 十二、设标准化变量\(X_1,X_2,X_3\)的相关阵为
\[R=\begin{bmatrix}
1.00 & 0.63 & 0.45 \\
0.63 & 1.00 & 0.35 \\
0.45 & 0.35 & 1.00
\end{bmatrix},
\]
(1)求\(m=2\)的主成分解,并计算因子\(F_1\)的贡献与\(X_2\)的共同度,计算因子模型的残差平方和。
(2)已知标准化后的样本\(X=(0.4, 0.5, 0.6)'\),求其巴特莱特因子得分与汤普森因子得分。
解:(1)\(R\)的特征值为
\[\lambda_1=1.9633,\quad \lambda_2=0.6795,
\]
对应单位正交向量为
\[a_1=\begin{bmatrix}
-0.625 \\ -0.593 \\ -0.507
\end{bmatrix},a_2=\begin{bmatrix}
0.219 \\ 0.491 \\ -0.873
\end{bmatrix}.
\]
所以
\[A=(\sqrt{\lambda_1}a_1,\sqrt{\lambda_2}a_2)=\begin{bmatrix}
-0.876 & 0.180 \\ -0.831 & 0.405 \\ -0.711 & -0.695
\end{bmatrix}.
\]
此时
\[AA'=\begin{bmatrix}
0.800 & 0.800 & 0.498 \\
0.800 & 0.855 & 0.309 \\
0.498 & 0.309 & 0.989
\end{bmatrix},D=\begin{bmatrix}
0.200 \\ & 0.145 \\ & &0.011
\end{bmatrix}.
\]
因子\(F_1\)的贡献为\(q_1^2=1.963\),变量\(X_2\)的共同度为\(h_2^2=0.855\)。此时
\[R-(AA'+D)=\begin{bmatrix}
0 & -0.171 & -0.048 \\
-0.171 & 0 & 0.041 \\
-0.048 & 0.041 & 0
\end{bmatrix},\quad Q=0.066.
\]
(2)使用加权最小二乘法计算巴特莱特因子得分,有
\[\hat F=(A'A)^{-1}A'X=\begin{bmatrix}
-0.607 \\ -0.210
\end{bmatrix},
\]
或者使用不加权最小二乘法计算因子得分,有
\[\hat F=(A'D^{-1}A)^{-1}A'D^{-1}X=\begin{bmatrix}
-0.627 \\ -0.220
\end{bmatrix}
\]
使用回归法计算汤普森因子得分,有
\[\hat F=A'R^{-1}X=\begin{bmatrix}
-0.607 \\ -0.210
\end{bmatrix}.
\]
可以看到,巴特莱特因子得分与汤普森因子得分几乎一致。
第十三题:典型相关分析
典型相关分析特例 十三、已知标准化变量的相关阵为
\[R=\begin{bmatrix}
R_{11} & R_{12} \\ R_{21} & R_{22}
\end{bmatrix}=\begin{bmatrix}
1 & \alpha & \beta & \beta \\
\alpha & 1 & \beta & \beta \\
\beta & \beta & 1 & \nu \\
\beta & \beta & \nu & 1
\end{bmatrix}.
\]
求\(X,Y\)的典型相关变量与典型相关系数。
解:先计算\(R_{11}\)和\(R_{22}\)的逆:
\[R_{11}^{-1}=\frac{1}{1-\alpha^2}\begin{bmatrix}
1 & -\alpha \\
-\alpha & 1
\end{bmatrix},\quad R_{22}^{-1}=\frac{1}{1-\nu^2}\begin{bmatrix}
1 & -\nu \\
-\nu & 1
\end{bmatrix}
\]
所以
\[R_{11}^{-1}R_{12}R_{22}^{-1}R_{21}=R_{22}^{-1}R_{21}R_{11}^{-1}R_{12}=\frac{2\beta^2}{(1+\alpha)(1+\nu)}\begin{bmatrix}
1 & 1 \\ 1 & 1
\end{bmatrix},
\]
于是
\[\lambda_1^2=\frac{4\beta^2}{(1+\alpha)(1+\nu)},\quad \lambda_2^2=0.
\]
对应于\(\lambda_1\)的特征向量为\((1,1)'\),故\(a_1=x(1,1)',b_1=y(1,1)'\),由\(a_1'R_{11}a_1=1\)和\(b_1'R_{22}b_1=1\)得到
\[x=\frac{1}{\sqrt{2(1+\alpha)}},\quad a_1=\frac{1}{\sqrt{2(1+\alpha)}}\begin{bmatrix}
1 \\ 1
\end{bmatrix};\\
y=\frac{1}{\sqrt{2(1+\nu)}},\quad b_1=\frac{1}{\sqrt{2(1+\nu)}}\begin{bmatrix}
1 \\ 1
\end{bmatrix}.
\]
典型相关变量为\(a_1X\)和\(b_1Y\),典型相关系数为
\[\rho_1=\frac{2\beta}{\sqrt{(1+\alpha)(1+\nu)}}.
\]
第十四题:典型相关分析实例
样本典型相关 十四、设标准化变量构成的相关系数阵为
\[R=\begin{bmatrix}
1.0 & 0.5 & 0.7 & 0.7 \\
0.5 & 1.0 & 0.7 & 0.7 \\
0.7 & 0.7 & 1.0 & 0.6 \\
0.7 & 0.7 & 0.6 & 1.0
\end{bmatrix},
\]
求:
(1)样本典型相关变量。有一个样本的标准化数值为\((0.1, 0.3, -0.2, 0.4)\),求其第一对典型相关得分。
(2)设\(X\)的典型相关变量为\(V=(V_1,V_2)'=A'X\),\(Y\)的典型相关变量为\(W=(W_1,W_2)=B'Y\),求\(V_1\)解释\(X\)的总变差百分比、\(W_1\)解释\(Y\)的总变差百分比,以及第一对典型变量中\(X\)的冗余测度。
解:(1)由上一题取\(\alpha=0.5,\nu=0.6,\beta=0.7\),已知其第一对典型相关变量的权重向量为
\[a_1=\begin{bmatrix}
0.577 \\ 0.577
\end{bmatrix},\quad b_1=\begin{bmatrix}
0.559 \\ 0.559
\end{bmatrix},
\]
容易解得
\[a_2=\begin{bmatrix}
1 \\ -1
\end{bmatrix},\quad b_2=\begin{bmatrix}
1.118 \\ -1.118
\end{bmatrix}.
\]
样本的第一对典型相关得分为\((0.2308,0.1118)\)。
(2)这里
\[A=\begin{bmatrix}
0.577 & 1 \\
0.577 & -1
\end{bmatrix},B=\begin{bmatrix}
0.559 & 1.118 \\ 0.559 & -1.118
\end{bmatrix}.
\\R_{11}A=\begin{bmatrix}
0.866 & 0.5 \\ 0.866 & 0.5
\end{bmatrix},R_{22}B=\begin{bmatrix}
0.894 & 0.447 \\ 0.894 & -0.447
\end{bmatrix}.
\]
\(V_1\)解释\(X\)的总变差百分比和\(W_1\)解释\(Y\)的总变差百分比为
\[R_d(X;V_1)=\frac{1}{2}\sum_{i=1}^2\rho^2(X_i, V_1)=0.750,\\
R_d(Y;W_1)=\frac{1}{2}\sum_{i=1}^2\rho^2(Y_i, W_1)=0.799.
\]
第一对典型变量中\(X\)的冗余测度为
\[R_{12}B=\begin{bmatrix}
0.7826 & 0 \\
0.7826 & 0
\end{bmatrix}
\\R_d(X;W_1)=\frac{1}{2}\sum_{i=1}^2\rho^2(X_i,W_1)=0.6125.
\]


