本文分为两个部分:三大模型五个具体分支的计算问题,重点证明。如果有时间,后续会出一个名词解释专题。
观前提示:本文系作者独立完成,审阅不足,如有发现错误,欢迎在评论区指正。
Part 1:具体模型计算
Part 1:AR(1)模型
稳定性条件
满足\({\rm AR}(1)\)模型的平稳序列被称为\({\rm AR(1)}\)序列,\({\rm AR}(1)\)模型的基本结构是
\[X_t=aX_{t-1}+\varepsilon_t,\quad |a|<1,\quad \{\varepsilon_t\}\sim {\rm WN}(0,\sigma^2).
\]
它有唯一平稳解。如果\(|a|>1\),则此模型不是\({\rm AR}(1)\)模型,参加以下两图。
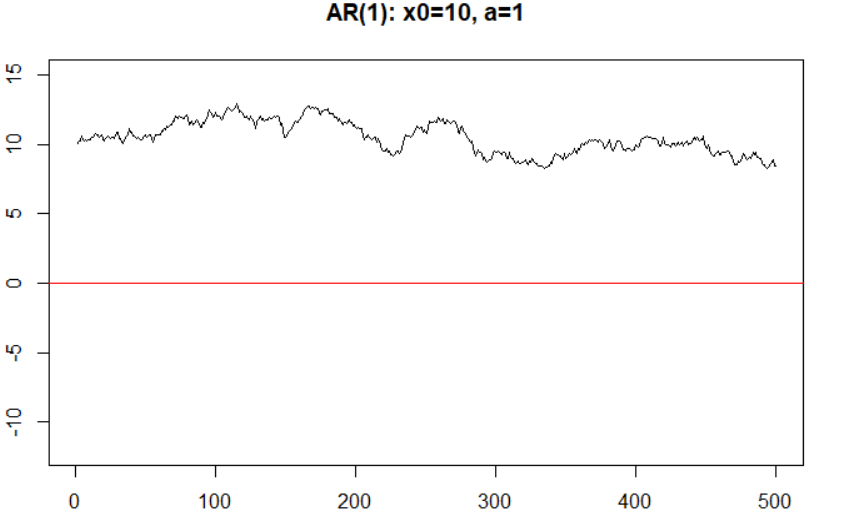
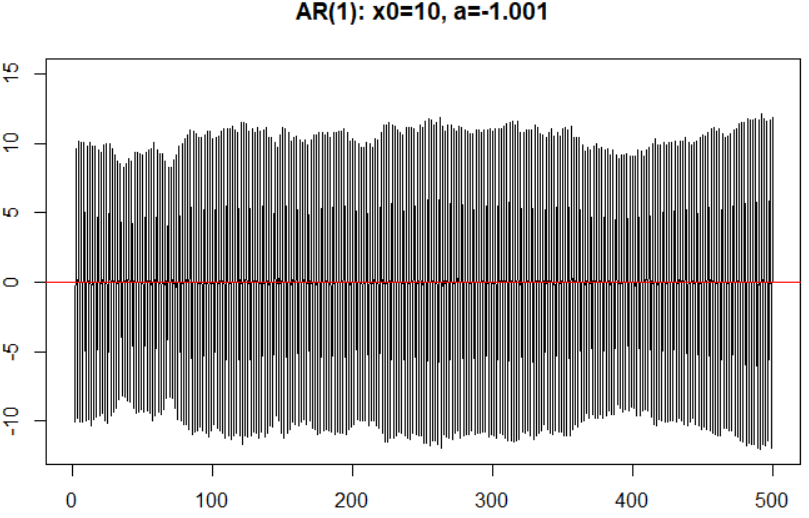
\({\rm AR}(1)\)序列的自协方差函数是其最显著性质,注意只有稳定性条件满足时,\(X_t\)才与\(\varepsilon_{t+k}\)无关(\(k>0\))。
\[\gamma_0=\frac{\sigma^2}{1-a^2}>\sigma^2,\\
\gamma_k=a^k\gamma_0\to 0,\quad k\ge 1,\\
a=\frac{\gamma_1}{\gamma_0}.
\]
证明:
对于\(\gamma_0\),有
\[\begin{aligned}
\gamma_0=&\mathbb{E}(X_t^2)\\
=&\mathbb{E}[(aX_{t-1}+\varepsilon_t)^2]\\
=&a^2\mathbb{E}(X_{t-1}^2)+\mathbb{E}(\varepsilon_t^2)\\
=&a^2\gamma_0+\sigma^2,
\end{aligned}
\]
故
\[\gamma_0=\frac{\sigma^2}{1-a^2}>\sigma^2.
\]
对于\(k\ge 1\)时的\(\gamma_k\),有
\[\gamma_k=\mathbb{E}(X_tX_{t-k})=\mathbb{E}[(aX_{t-1}+\varepsilon_t)X_{t-k}]=a\gamma_{k-1}.
\]
由数学归纳法,有
\[\gamma_k=a^k\gamma_0\to 0.
\]
\({\rm AR}(1)\)序列的谱密度:
\[\begin{aligned}
f(\lambda)=&\frac{\sigma^2}{2\pi|1-ae^{{\rm i}\lambda}|^2} \\
=&\frac{\sigma^2}{2\pi|1-a\cos\lambda-{\rm i}a\sin\lambda|^2}\\
=&\frac{\sigma^2}{2\pi(1-2a\cos\lambda+a^2)}.
\end{aligned}
\]
偏相关系数截尾
递推\({\rm AR}(1)\)序列的偏相关系数:
\[a_{1,1}\ne0,\quad a_{k,k}=0,\quad \forall k>1.
\]
当\(k=1\)时,由Yule-Walker方程,
\[\gamma_0a_{1,1}=\gamma_1,
\]
得到\(a_{1,1}=\gamma_1/\gamma_0=a\ne 0\)。
由Yule-Walker方程,
\[\begin{bmatrix}
1 & a & \cdots & a^{n-1} \\
a & 1 & \cdots & a^{n-2} \\
\vdots & \vdots & & \vdots \\
a^{n-1} & a^{n-2} & \cdots & 1
\end{bmatrix}\begin{bmatrix}
a_{n,1} \\ a_{n,2} \\ \vdots \\ a_{n,n}
\end{bmatrix}=\begin{bmatrix}
a \\ a^2 \\ \vdots \\ a^{n}
\end{bmatrix}=a\begin{bmatrix}
1 \\ a \\ \vdots \\ a^{n-1}
\end{bmatrix}.
\]
注意到右端向量与左端系数矩阵第一列相同,由Cramer法则,有\(a_{n,2}=\cdots=a_{n,n}=0\),而\(a_{n,1}=\det(\Gamma_n)/\det(\Gamma_n)=a\),结论得证。
Part 2:AR(2)模型
稳定性条件
满足\({\rm AR}(2)\)模型的平稳序列称为\({\rm AR}(2)\)序列,\({\rm AR}(2)\)模型形如
\[X_t=a_1X_{t-1}+a_2X_{t-2}+\varepsilon_t.
\]
其中,特征方程\(A(z)=1-a_1z-a_2z^2\)在\(|z|\le 1\)内没有根。
\({\rm AR}(2)\)模型的稳定域\(\mathscr A\)为
\[\mathscr A=\{(a_1,a_2)|a_2\pm a_1<1,|a_2|<1 \}.
\]
即找到\(f(z)=a_2z^2+a_1z-1\)在\(|z|\le 1\)内没有根的条件,注意到\(f(0)=-1\)。
-
如果抛物线开口朝上,则\(a_2>0\),由零点存在定理,只需
\[f(1)=a_2+a_1-1<0,\\
f(-1)=a_2-a_1-1<0.
\]
即:
\[a_2>0\text{ & }a_2\pm a_1<1.
\]
-
如果抛物线开口朝下,则\(a_2<0\),对称轴符号与\(a_1\)的一致,先讨论方程组无实根的情况,此时\(\Delta=a_1^2+4a_2<0\),两个复根是
\[z=\frac{-a_1\pm{\rm i}\sqrt{-a_1^2-4a_2}}{2a_2},
\]
要使其模长\(|z|>1\),有
\[\frac{a_1^2-a_1^2-4a_2}{4a_2^2}=-\frac{1}{a_2}>1.
\]
所以\(a_2>-1\),即:
\[-1<a_2<0.
\]
-
最后考虑\(a_2<0\)且\(\Delta>0\)的情况,对对称轴分情况讨论。
-
如果\(a_1>0\),则对称轴是正数,所以要满足\(f(1)<0\),对称轴\(>1\),即
\[a_2+a_1<1\text{ & }a_1>-2a_2.
\]
-
如果\(a_1<0\),则对称轴是负数,所以要满足\(f(-1)<0\),对称轴\(<-1\),即
\[a_2-a_1<1\text{ & }a_1<2a_2.
\]
综合以上条件,要使得\(A(z)\)的根都在单位圆外,必须有\(a_2\pm a_1<1\)且\(|a_2|<1\),图示如下:
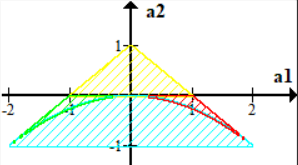
这里,黄色部分对应1中的讨论,蓝色部分对应2中的讨论,红色和绿色部分对应3中的讨论。有几下几点需要注意:
- 如果\(a_1,a_2\)位于蓝色部分,则此时的根是虚根(结合讨论可以看出)。
- 证明过程的讨论是在有实根时,对四个象限分别讨论,无实根时单独讨论。
- 对于复根部分要额外注意,需要满足复根也在单位圆外(容易被忽视),否则得到的稳定域会多出\(\mathbb{R}\)上抛物线下方的部分。
- 这里没有对\(a_1=0\)或\(a_2=0\)的情况作讨论,其讨论难度小,所以不作说明。
自相关函数与允许域
\({\rm AR}(2)\)序列的自协方差函数当\(k\ge2\)时也满足特征多项式差分方程,即
对于\(k=0,1\),有
\[\begin{aligned}
\gamma_0=&\mathbb{E}(X_t^2)\\
=&\mathbb{E}[(a_1X_{t-1}+a_2X_{t-2}+\varepsilon_t)^2]\\
=&\mathbb{E}(a_1^2X_{t-1}^2+a_2^2X_{t-2}^2+\varepsilon_t^2+2a_1a_2X_{t-1}X_{t-2})\\
=&(a_1^2+a_2^2)\gamma_0+\sigma^2+2a_1a_2\gamma_1,\\
\gamma_1=&\mathbb{E}(X_tX_{t-1})\\
=&\mathbb{E}[(a_1X_{t-1}+a_2X_{t-2}+\varepsilon_t)X_{t-1}]\\
=&a_1\gamma_0+a_2\gamma_1,
\end{aligned}
\]
所以
\[\gamma_1=\frac{a_1}{1-a_2}\gamma_0,\\
\gamma_0=\frac{\sigma^2}{1-a_2^2-a_1^2(1-\frac{2a_2}{1-a_2})}.
\]
对于\(k\ge 2\),有
\[\begin{aligned}
\gamma_k=&\mathbb{E}[X_{t-k}X_t]\\
=&\mathbb{E}[X_{t-k}(a_1X_{t-1}+a_2X_{t-2}+\varepsilon_t)]\\
=&a_1\gamma_{k-1}+a_2\gamma_{k-2}.
\end{aligned}
\]
注意到\(\gamma_0\)求解不易,所以考虑\({\rm AR}(2)\)序列的自相关函数,有
\[\rho_1=\frac{a_1}{1-a_2},\rho_2=\frac{a_1^2}{1-a_2}+a_2, \\
\rho_k=a_1\rho_{k-1}+a_2\rho_{k-2},\quad \forall k\ge 2.
\]
\({\rm AR}(2)\)序列的允许域:\((\rho_1,\rho_2)\)可以由\((a_1,a_2)\)表示,根据\((a_1,a_2)\)的范围可以推出\((\rho_1,\rho_2)\)的范围,即允许域,但这不是一个线性变换。
\[\mathscr{C}=\{(\rho_1,\rho_2)|\rho_1^2<(1+\rho_2)/2,|\rho_1|<1,|\rho_2|<1\}.
\]
由自协方差函数的有界性,有\(|\rho_1|<1\),\(|\rho_2|<1\)。而
\[\rho_1=\frac{a_1}{1-a_2},\\
\rho_2=\frac{a_1^2}{1-a_2}+a_2,
\]
得
\[a_1=\frac{\rho_1(1-\rho_2)}{1-\rho_1^2},\\
a_2=\frac{\rho_2-\rho_1^2}{1-\rho_1^2}.
\]
所以由\(a_2-a_1<1\)有
\[\frac{\rho_2-\rho_1^2-\rho_1(1-\rho_2)}{1-\rho_1^2}<1\Rightarrow \rho_2<1,
\]
由\(a_2+a_1<1\)有
\[\frac{\rho_2-\rho_1^2+\rho_1-\rho_1\rho_2}{1-\rho_1^2}<1\Rightarrow \rho_2<1,
\]
由\(a_2<1\)有
\[\rho_2-\rho_1^2<1-\rho_1^2\Rightarrow \rho_2<1,
\]
由\(a_2>-1\)有
\[\rho_2-\rho_1^2>\rho_1^2-1\Rightarrow \rho_1^2<\frac{1+\rho_2}{2}<1.
\]
完成此处的证明关键在于找到\(a_1,a_2\)与\(\rho_1,\rho_2\)相互表达的式子,这可以由Yule-Walker方程得到,即
\[\begin{bmatrix}
1 & \rho_1 \\ \rho_1 & 1
\end{bmatrix}\begin{bmatrix}
a_1 \\ a_2
\end{bmatrix}=\begin{bmatrix}
\rho_1 \\ \rho_2
\end{bmatrix},\\
\begin{bmatrix}
a_1 \\ a_2
\end{bmatrix}=\frac{1}{1-\rho_1^2}
\begin{bmatrix}
1 & -\rho_1 \\ -\rho_1 & 1
\end{bmatrix}\begin{bmatrix}
\rho_1 \\ \rho_2
\end{bmatrix}=\begin{bmatrix}
\frac{\rho_1-\rho_1\rho_2}{1-\rho_1^2} \\
\frac{\rho_2-\rho_1^2}{1-\rho_1^2}
\end{bmatrix}.
\]
实根不相等时的自相关函数通项
如果\(A(z)=1-a_1z-a_2z^2\)有两个不等实根,则\(f(\lambda)=\lambda^2-a_1\lambda-a_2\)有两个不等实根\(\lambda_1,\lambda_2\),且
\[\lambda_1=\frac{1}{z_1},\quad \lambda_2=\frac{1}{z_2}.
\\
|\lambda_1|<1,\quad |\lambda_2|<1.
\]
由于自相关函数满足
\[\rho_k=a_1\rho_{k-1}+a_2\rho_{k-2},\quad \forall k\ge2,
\]
所以由常系数齐次线性差分方程的求解,有
\[\rho_k=c_1\lambda_1^k+c_2\lambda_2^k,
\]
代入\(\rho_0,\rho_1\)的值,有
\[c_1+c_2=\rho_0=1,\\
c_1\lambda_1+c_2\lambda_2=\rho_1,
\]
从中可以解得
\[c_1=\frac{\lambda_2-\rho_1}{\lambda_2-\lambda_1},\quad c_2=\frac{\rho_1-\lambda_1}{\lambda_2-\lambda_1}.
\]
由韦达定理,代入得
\[\rho_1=\frac{a_1}{1-a_2}=\frac{\lambda_1+\lambda_2}{1+\lambda_1\lambda_2},\\
c_1=\frac{\lambda_1(1-\lambda_2^2)}{(\lambda_1-\lambda_2)(1+\lambda_1\lambda_2)},\quad c_2=\frac{\lambda_2(1-\lambda_1^2)}{(\lambda_2-\lambda_1)(1+\lambda_1\lambda_2)},
\]
所以
\[\rho_k=c_1\lambda_1^k+c_2\lambda_2^k=\frac{(1-\lambda_2^2)\lambda_1^{k+1}-(1-\lambda_1^2)\lambda_2^{k+1}}{(\lambda_1-\lambda_2)(1+\lambda_1\lambda_2)},\quad k\ge0.
\]
偏相关系数截尾
正向证明:由Yule Walker方程,只要证明以下三个向量线性相关:
\[\boldsymbol{v}_1=(1,\rho_1,\cdots,\rho_{n-1}),\\
\boldsymbol{v}_2=(\rho_1,1,\rho_1,\cdots,\rho_{n-2}),\\
\boldsymbol{v}_n=(\rho_1,\rho_2,\cdots,\rho_n).
\]
也只要证明以下等式成立:
\[\boldsymbol {v}_n=a_1\boldsymbol v_1+a_2\boldsymbol v_2.
\]
由自相关函数的递推式,后\(n-1\)项都是显然的,而
\[\rho_1=\frac{a_1}{1-a_2}\Rightarrow \rho_1=a_1+a_2\rho_1,
\]
所以这就证明了以上三个向量线性相关,即\(\forall n\)与\(m>2\),有\(a_{n,m}=0\)。由此表达式,也有
\[a_{n,1}=a_1,\quad a_{n,2}=a_2.
\]
递推预测
显然\(\hat X_1=0\),\(\hat X_2=L(X_2|X_1)=\rho_1 X_1=\frac{a_1}{1-a_2}X_1\)。
对于\(n\ge 3\),由预测方程可以算出
\[\hat X_{n}=a_1X_{n-1}+a_2X_{n-2},
\]
这是因为Yule-Walker方程给出的形式与预测方程一致。
Part 3:MA(1)模型
基本信息
满足\({\rm MA}(1)\)模型的平稳序列称为\({\rm MA}(1)\)序列,其基本形式是
\[X_t=\varepsilon_t+b\varepsilon_{t-1},\quad \{\varepsilon_t\}\sim{\rm WN}(0,\sigma^2), \quad |b|\le 1.
\]
其自协方差函数是\(1\)后截尾的:
\[\gamma_0=(1+b^2)\sigma^2,\quad \gamma_1=b\sigma^2,\\
\rho_1=\frac{b}{1+b^2}<1.
\]
由于\(|b|\le 1\),所以在\([-1,1]\)内,
\[\frac{{\rm d}\rho_1}{{\rm d}b}=\frac{1-b^2}{(1+b^2)^2}>0,
\]
即\(\rho_1\)随\(b\)变化是单调的,所以
\[\rho_1\in\left[-\frac12,\frac12\right].
\]
谱密度:
\[f(\lambda)=\frac{1}{2\pi}\sum_{j=-1}^1\gamma_k e^{-{\rm i}j\lambda}=\frac{\sigma^2}{2\pi}(2b\cos \lambda+1+b^2).
\]
注意:以下序列也是\({\rm MA}(1)\)序列,因为其自协方差函数1后截尾,但是模型系数并非现在的系数:
\[X_t=\epsilon_t+3\epsilon_{t-1},\quad \epsilon\sim {\rm WN}(0,\sigma^2)
\]
计算其谱密度,有
\[\begin{aligned}
f(\lambda)=&\frac{\sigma^2}{2\pi}\left|1+3e^{{\rm i}\lambda} \right|^2\\
=&\frac{\sigma^2}{2\pi}(1+3^2+6\cos \lambda)\\
=&\frac{9\sigma^2}{2\pi}\left(1+\frac{2}{3}\cos \lambda+\frac{1}{9} \right)\\
=&\frac{9\sigma^2}{2\pi}\left|1+\frac{1}{3}e^{{\rm i}\lambda} \right|^2
\end{aligned}
\]
所以它满足的\({\rm MA(1)}\)模型是
\[X_t=\varepsilon_t+\frac{1}{3}\varepsilon_{t-1},\quad \varepsilon_t\sim {\rm WN}(0,3\sigma).
\]
这里\(\varepsilon_t\)并非与\(\epsilon_t\)独立的白噪声,而是通过以下方式构造的:
\[\varepsilon_t=(1+\frac{1}{3}\mathscr B)^{-1}X_t=\sum_{j=0}^\infty \frac{1}{(-3)^j}X_{t-j}.
\]
这样就有
\[\begin{aligned}
\varepsilon_t+\frac13\varepsilon_{t-1}=&\sum_{j=0}^\infty\frac{1}{(-3)^j}X_{t-j}+\frac{1}3\sum_{j=0}^\infty\frac{1}{(-3)^j}X_{t-j-1}\\
=&\sum_{j=0}^\infty\frac{1}{(-3)^j}X_{t-j}+\sum_{j=1}^\infty\frac{1}{-(-3)^j}X_{t-j} \\
=&X_t.
\end{aligned}
\]
同时
\[f_\varepsilon(\lambda)=\left|\frac{1}{1+\frac13e^{{\rm i}\lambda}}\right|^2f(\lambda)=\frac{9\sigma^2}{2\pi}\left|\frac{1+\frac{1}{3}e^{{\rm i}\lambda}}{1+\frac13e^{{\rm i}\lambda}} \right|^2=\frac{9\sigma^2}{2\pi},
\]
谱密度是常数就说明了\(\varepsilon_t\)是白噪声。
偏相关系数不截尾
\({\rm MA}(1)\)的偏相关系数满足:
\[a_{k,k}=-(-b)^k(1-b^2)(1-b^{2k+2})^{-1}.
\]
由于\(\rho_1=\frac{b}{1+b^2}\xlongequal{d}\rho\),对\(k>1\)有\(\rho_k=0\),由Yule Walker方程,有
\[\begin{bmatrix}
1 & \rho & 0 & \cdots & 0 \\
\rho & 1 & \rho & \cdots & 0 \\
0 & \rho & 1 & \cdots & 0 \\
\vdots & \vdots & \vdots & & \vdots \\
0 & 0 & 0 & \cdots &1
\end{bmatrix}\begin{bmatrix}
a_{n,1} \\ a_{n,2} \\ a_{n,3} \\ \vdots \\ a_{n,n}
\end{bmatrix}=\begin{bmatrix}
\rho \\ 0 \\ 0 \\ \vdots \\ 0
\end{bmatrix}.
\]
记\(n\)阶系数矩阵的行列式为\(D_n\),则显然有
\[D_n=D_{n-1}-\rho^2D_{n-2},
\]
构成一个常系数线性差分方程,特征方程是
\[z^2-z+\rho^2=0,
\]
其特征根是
\[z_1=\frac{1+\sqrt{1-4\rho^2}}{2},\quad z_2=\frac{1-\sqrt{1-4\rho^2}}{2},
\]
所以通解为
\[D_n^*=c_1z_1^n+c_2z_2^n,
\]
又因为\(D_1=1,D_2=1-\rho^2\),所以
\[D_n=\frac{z_1^{n+1}-z_2^{n+1}}{z_1-z_2}.
\]
由Cramer法则,
\[a_{n,n}=\frac{-(-1)^n\rho^n}{D_n}.
\]
这就证明了偏相关系数不截尾,因为\(b \ne 0\)即\(\rho=0\)。
事实上,
\[|D_n|=\frac{1+b^2+\cdots+b^{2n}}{(1+b^2)^n}=\frac{1-b^{2n+2}}{(1+b^2)^n(1-b^2)},
\]
对\(D_1,D_2\)显然,此后
\[\begin{aligned}
D_{n-1}-\rho^2D_{n-2}=&\frac{1-b^{2n}}{(1+b^2)^{n-1}(1-b^2)}-\frac{b^2(1-b^{2n-2})}{(1+b^2)^n(1-b^2)}\\
=&\frac{1+b^2-b^{2n}-b^{2n+2}-b^2+b^{2n}}{(1+b^2)^{n}(1-b^2)}\\
=&\frac{1-b^{2n+2}}{(1+b^2)^n(1-b^2)}.
\end{aligned}
\]
这就得到
\[a_{n,n}=\frac{-(-1)^nb^n(1-b^2)}{1-b^{2n+2}}.
\]
递推预测
对于\({\rm MA}(1)\)序列
\[X_t=\varepsilon_t+b\varepsilon_{t-1},\quad b\le 1.
\]
其预测系数是\(q\)截尾的。
记\(\boldsymbol X_n=(X_1,\cdots,X_n)'\),样本信息序列为\(Z_i\),\(\boldsymbol Z_n=(Z_1,\cdots,Z_n)'\),则它们的张成空间相同(这一点可以由归纳法证明),所以
\[L(X_{n+1}|\boldsymbol X_n)=L(X_{n+1}|X_n,\cdots,X_{n-q+1})=\cdots=L(X_{n+1}|Z_n,\cdots,Z_{n-q+1}).
\]
这说明只需要使用\(q\)个新息即可,故\(k\ge q\)时\(\theta_{n,k}=0\)。
并且:
\[\theta_{n,1}=b\sigma^2\nu_{n-1}^{-1}\\
\nu_0=(1+b^2)\sigma^2,\\
\nu_n=\sigma^2(1+b^2-b^2\sigma^2\nu_{n-1}^{-1}).
\]
由于\(\hat X_{n+1}=\theta_{n,1}(X_n-\hat X_n)\),两边同时乘以\((X_n-\hat X_{n})\)并取期望,有
\[\begin{aligned}
&\mathbb{E}[\hat X_{n+1}(X_n-\hat X_{n})] \\
=&\mathbb{E}[X_{n+1}-(X_{n+1}-\hat X_{n+1})](X_n-\hat X_n) \\
=&\gamma_1 \\
=&\theta_{n,1}\mathbb{E}(X_n-\hat X_n)^2 \\
=&\theta_{n,1}\nu_{n-1}.
\end{aligned}
\]
所以
\[\theta_{n,1}=\frac{\gamma_1}{\mathbb{E}(X_n-\hat X_n)^2}=\frac{b\sigma^2}{\nu_{n-1}}.
\]
结合均方误差递推公式:
\[\nu_n=\gamma_0-\theta_{n,1}^2\nu_{n-1}=(1+b^2)\sigma^2-\frac{b^2\sigma^4}{\nu_{n-1}},
\]
可以得到\(\theta_{n,1}\)的计算值。
以下给出一些\(\theta_{n,1}\)的计算值:
-
\(\theta_{1,1}\):
\[\theta_{1,1}=\gamma^{-1}_0\gamma_1=\frac{b}{1+b^2};
\]
-
\(\nu_1\):
\[\nu_1=\gamma_0-\theta_{1,1}^2\nu_0=\frac{1+b^2+b^4}{1+b^2}\sigma^2.
\]
-
\(\theta_{2,1}\):
\[\theta_{2,1}=\frac{b\sigma^2}{\nu_1}=\frac{b(1+b^2)}{1+b^2+b^4};
\]
-
\(\nu_2\):
\[\nu_2=\gamma_0-\theta_{2,1}^2\nu_1=\frac{1+b^2+b^4+b^6}{1+b^2+b^4}\sigma^2.
\]
-
令\(\mathcal B_n=1+b^2+\cdots+b^{2n}=\frac{1-b^{2n+2}}{1-b^2}\),则
\[\theta_{n,1}=\frac{b\mathcal B_{n-1}}{\mathcal B_n},\quad \nu_n=\frac{\sigma^2\mathcal B_{n+1}}{\mathcal B_n}.
\]
可以证明
\[\begin{aligned}
\nu_n=&(1+b^2)\sigma^2-\frac{b^2\mathcal B_{n-1}^2}{\mathcal B_{n}^2}\cdot\frac{\sigma^2\mathcal B_n}{\mathcal B_{n-1}} \\
=&\sigma^2\left[1+b^2\left(1-\frac{\mathcal B_{n-1}}{\mathcal B_n}\right) \right]\\
=&\sigma^2\left[1+b^2\cdot\frac{b^{2n}}{\mathcal B_n} \right]\\
=&\sigma^2\frac{\mathcal B_{n+1}}{\mathcal B_n};\\
\theta_{n,1}=&\frac{b\sigma^2}{\nu_{n-1}}\\
=&\frac{b\mathcal B_{n-1}}{\mathcal B_n}.
\end{aligned}
\]
Part 4:MA(2)模型
基本信息与稳定性条件
满足\({\rm MA}(2)\)模型的平稳序列称为\({\rm MA}(2)\)序列,\({\rm MA}(2)\)模型即满足
\[X_t=\varepsilon_t+b_1\varepsilon_{t-1}+b_2\varepsilon_{t-2}.
\]
这里,特征多项式\(B(z)=1+b_1z+b_2z^2\)在\(|z|<1\)内无根,特别当它在单位圆上也无根时称为可逆的。可逆域为
\[\mathscr I=\{(b_1,b_2):b_2\pm b_1>-1,|b_2|<1\}.
\]
注意到\(B(0)=1\),所以当开口向下即\(b_2<0\)时,一定有两个根,并且对称轴方向与\(b_1\)一致。
-
当\(b_2<0\)时,只需要\(B(1)>0\)且\(B(-1)>0\),即
\[b_2<0\text{ & }b_2\pm b_1>-1.
\]
-
当\(b_2>0\)时,先讨论无实根的情况,此时\(\Delta=b_1^2-4b_2<0\),两个复根是
\[z_{1,2}=\frac{-b_1\pm{\rm i}\sqrt{4b_2-b_1^2}}{2b_2},
\]
其模长为
\[|z|^2=z_1z_2=\frac{1}{b_2}>1,
\]
所以
\[0<b_2<1\text{ & }\Delta <0.
\]
-
当\(b_2>0\)时,对称轴方向与\(b_1\)不一致。如果有实根,则分两种情况考虑:
-
\(b_1<0\),即对称轴大于0时,必有
\[-\frac{b_1}{2b_2}>1,\quad B(1)>0,
\]
即
\[b_1<0\text{ & }b_2>0\text{ & }b_1+2b_2<0\text{ & }b_2+b_1>-1\text{ & }\Delta >0.
\]
-
\(b_1>0\),即对称轴小于0时,必有
\[-\frac{b_1}{2b_2}<-1,\quad B(-1)>0,
\]
即
\[b_1>0\text{ & }b_2>0\text{ & }b_1-2b_2>0\text{ & }b_2-b_1>-1\text{ & }\Delta >0.
\]
综合以上讨论就得到了可逆域。
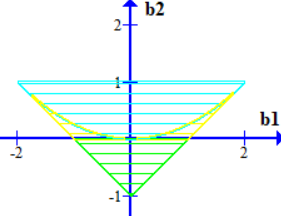
上图中,绿色为第一部分,蓝色为第二部分(即复根),黄色为第三部分。
基本数字特征:
\[\gamma_0=\sigma^2(1+b_1^2+b_2^2),\quad \gamma_1=\sigma^2(b_1+b_1b_2),\quad \gamma_2=\sigma^2b_2;\\
\rho_1=\frac{b_1+b_1b_2}{1+b_1^2+b_2^2},\quad \rho_2=\frac{b_2}{1+b_1^2+b_2^2},\\
\forall k>2,\quad \rho_k=\gamma_k=0.
\]
谱密度:
\[f(\lambda)=\frac{\sigma^2}{2\pi}\left|1+b_1e^{{\rm i}\lambda}+b_2e^{2{\rm i}\lambda} \right|^2.
\]
Part 5:ARMA(1, 1)模型
基本信息
模型特征:
\[X_t=aX_{t-1}+\varepsilon_t+b\varepsilon_{t-1}.
\]
自协方差函数:
\[\gamma_0=\frac{\sigma^2(1+2ab+b^2)}{1-a^2},\quad \rho_1=\frac{(a+b)(ab+1)}{1+2ab+b^2},\\
\forall k\ge 2,\quad \rho_k=a\rho_{k-1}=\cdots=a^{k-1}\rho_1.
\]
对于\(k=0\),有
\[\begin{aligned}
\mathbb{E}(X_t\varepsilon_t)=&\mathbb E[\varepsilon_t(aX_{t-1}+\varepsilon_t+b\varepsilon_{t-1})]\\
=&\sigma^2,\\
\gamma_0=&\mathbb{E}(X_t^2)=\mathbb{E}[(aX_{t-1}+\varepsilon_t+b\varepsilon_{t-1})^2]\\
=&a^2\gamma_0+(1+b^2+2ab)\sigma^2,\\
\gamma_0=&\frac{\sigma^2(1+2ab+b^2)}{1-a^2}.
\end{aligned}
\]
对于\(k=1\),有
\[\begin{aligned}
\gamma_1=&\mathbb{E}(X_tX_{t-1})=\mathbb{E}[(aX_{t-1}+\varepsilon_t+b\varepsilon_{t-1})X_{t-1}]\\
=&a\gamma_0+b\sigma^2, \\ \\
\rho_1=&\frac{\gamma_1}{\gamma_0}\\
=&a+\frac{b\sigma^2}{\gamma_0}\\
=&\frac{(a+b)(ab+1)}{1+2ab+b^2}.
\end{aligned}
\]
对于\(k\ge 2\),有
\[\gamma_k=\mathbb{E}(X_tX_{t-k})=\mathbb{E}[(aX_{t-1}+\varepsilon_t+b\varepsilon_{t-1})X_{t-k}]=a\gamma_{k-1},\\
\rho_k=a\rho_{k-1}=\cdots=a^{k-1}\rho_1.
\]
谱密度:
\[f(\lambda)=\frac{\sigma^2}{2\pi}\left|\frac{1+be^{{\rm i}\lambda}}{1-ae^{{\rm i}\lambda}} \right|^2.
\]
此时的谱密度被称为有理谱密度。
\({\rm ARMA}(1, 1)\)模型具有Wold表示:
\[X_t=\sum_{j=0}^\infty \psi_j\varepsilon_{t-j}.
\]
Wold系数可以递推计算:定义\(\forall j>q:b_j=0\),则
\[\forall k<0:\psi_k=0,\quad \psi_0=1,\\
\forall k>0:\psi_k=b_k+\sum_{j=0}^pa_j\psi_{k-j}.
\]
最佳线性预测
作以下变换:
\[Y_t=\left\{\begin{array}l
X_t/\sigma,&t=1; \\
(X_t-aX_{t-1})/\sigma,& t>1.
\end{array}\right.
\]
\(Y_t\)的样本新息与\(X_t\)的样本新息只差一个\(\sigma\)。对\(t\le1\),
\[\mathbb{E}(Y_1^2)=\frac{1}{\sigma^2}\mathbb{E}(X_t^2)=\frac{1+2ab+b^2}{1-a^2},
\]
对于\(t\ge 2\),
\[\mathbb{E}(Y_t^2)=\frac{1}{\sigma^2}\mathbb{E}(\varepsilon_t+b\varepsilon_{t-1})^2=1+b^2,
\]
对于\(s=2\),\(t=1\),
\[\mathbb{E}(Y_2Y_1)=\frac{1}{\sigma^2}\mathbb{E}[X_1(\varepsilon_2+b\varepsilon_1)]=b,
\]
对于\(s-t=1\),
\[\mathbb{E}(Y_{t+1}Y_t)=\frac1{\sigma^2}\mathbb{E}[(\varepsilon_{t+1}+b\varepsilon_{t})(\varepsilon_t+b\varepsilon_{t-1})]=b,
\]
其他情况下
\[\mathbb{E}(Y_sY_t)=0.
\]
显然\(\hat Y_1=0\),\(\hat Y_2=\theta_{1,1}Y_1\),这里
\[\theta_{1,1}=\frac{\mathbb{E}(Y_1Y_2)}{\mathbb{E}(Y_1^2)}=\frac{(1-a^2)b}{1+2ab+b^2}.
\]
由于从\(k=2\)开始\(\{Y_k\}\)是一个\({\rm MA}(1)\)序列,所以\(\hat Y_{n+1}=\theta_{n,1}Y_n\),两边同时乘以\((Y_n-\hat Y_n)\)并取期望,得到
\[b=\theta_{n,j}\nu_{n-1},(\nu_{n-1}\xlongequal{def}\mathbb{E}(Y_n-\hat Y_n)^2),\\
\theta_{n,j}=\frac{b}{\nu_{n-1}},\\
\nu_n=(1+b^2)-\frac{b^2}{\nu_{n-1}}.
\]
最后,从\(Y_t\)反推\(X_t\)的递推,得到
\[\forall t > 2:\hat X_t=\sigma\hat Y_t+aX_{t-1}=\theta_{t-1,1}(X_{t-1}-\hat X_{t-1})+aX_{t-1}.
\]
Part 2:重要定理证明
自协方差函数的正定性
谱密度:如果\(\{X_t\}\)的谱密度\(f(\lambda)\)存在,则对任何\(n\ge 1\),\(\Gamma_n\)正定。
对任何\(n\)维实向量\(\boldsymbol{b}=(b_1,\cdots,b_n)'\),关于\(\lambda\)的函数
\[\sum_{k=1}^n b_ke^{{\rm i}k\lambda}
\]
最多只有\(n-1\)个零点(可以看成\(x=e^{{\rm i}\lambda}\)的一个关于\(x\)的多项式)。由于
\[\gamma_0=\int_{-\pi}^{\pi}f(\lambda){\rm d}\lambda>0,
\]
所以
\[\begin{aligned}
\boldsymbol{b}'\Gamma_{n}\boldsymbol b=&\sum_{j=1}^n\sum_{k=1}^n b_j\gamma_{j-k}b_k \\
=&\sum_{j=1}^n\sum_{k=1}^nb_jb_k\int_{-\pi}^\pi f(\lambda)e^{{\rm i}(k-j)\lambda}{\rm d}\lambda \\
=&\int_{-\pi}^{\pi}f(\lambda)\sum_{j=1}^n\sum_{k=1}^n b_jb_ke^{{\rm i}(k-j)\lambda}{\rm d}\lambda \\
=&\int_{-\pi}^{\pi}\left|\sum_{k=1}^n b_ke^{{\rm i}k\lambda} \right|^2f(\lambda){\rm d}\lambda\\
>&0.
\end{aligned}
\]
正定性得证。
自协方差函数收敛:如果\(\gamma_k\to 0(k\to \infty)\),则对任何\(n\ge 1\),\(\Gamma_n\)正定。
用反证法,如果\(|\Gamma_{n+1}|=0\)而\(|\Gamma_n|\ne 0\),对零均值平稳序列\(\{X_t\}\),定义
\[\boldsymbol{X}_n=(X_1,\cdots,X_n)',
\]
对任何实向量\(\boldsymbol{b}=(b_1,\cdots,b_n)'\ne 0\),有
\[\mathbb{E}(\boldsymbol{b}'\boldsymbol {X}_n)^2=\boldsymbol b'\Gamma_n\boldsymbol b>0.
\]
同时存在另一组\(\boldsymbol{a}=(a_1,\cdots,a_n,a_{n+1})'\ne 0\),使得
\[\mathbb{E}(\boldsymbol{a}'\boldsymbol{X}_{n+1})^2=\boldsymbol{a}'\Gamma_{n+1}\boldsymbol{a}=0.
\]
这说明\(X_{n+1}\)可以被\(\boldsymbol{X}_n\)线性表示,由\(\{X_t\}\)的平稳性,\(\forall k\ge 1\),\(X_{n+k}\)也能被\(\boldsymbol{X}=(X_n,\cdots, X_1)'\)线性表示,即存在一个\(\boldsymbol{\alpha}=(\alpha_1,\cdots,\alpha_n)'\),使得
\[X_{n+k}=\boldsymbol \alpha'\boldsymbol{X}.
\]
令\(0<\lambda_1\le \lambda_2\le \cdots\le\lambda_n\)为\(\Gamma_n\)的特征值,则存在正交矩阵\(T\),使得
\[T\Gamma_nT'={\rm diag}(\lambda_1,\cdots,\lambda_n).
\]
此时
\[\begin{aligned}
\gamma_0=&\mathbb{E}(X_{n+k}^2)=\mathbb{E}(\boldsymbol{\alpha}'\boldsymbol{X})^2\\
=&\boldsymbol\alpha'\Gamma_n\boldsymbol \alpha\\
=&(T\boldsymbol \alpha)'T\Gamma_nT'(T\boldsymbol\alpha)\\
\ge&\lambda_1\|T\boldsymbol \alpha\|^2\\
=&\lambda_1\|\boldsymbol{\alpha}\|^2.\\
\|\alpha\|\le &\frac{\gamma_0}{\gamma_1}.
\end{aligned}
\]
另一方面,有
\[\begin{aligned}
\gamma_0=&\mathbb{E}(\boldsymbol\alpha'\boldsymbol XX_{n+k})\\
=&\boldsymbol\alpha'\mathbb{E}(\boldsymbol XX_{n+k})\\
=&\boldsymbol\alpha'(\gamma_{k},\gamma_{k+1},\cdots,\gamma_{n+k-1})'\\
\le &\|\boldsymbol\alpha\|\sqrt{\sum_{j=0}^{n-1}\gamma_{k+j}^2}\\
\le& \left(\frac{\gamma_0}{\gamma_1}\sum_{j=0}^{n-1}\gamma_{k+j}^2 \right) \\
\to &0,\quad k\to \infty.
\end{aligned}
\]
这与\(\gamma_0>0\)矛盾。
推论:线性平稳序列的自协方差矩阵总是正定的。
简单离散谱序列的自协方差函数是三阶退化的。
简单离散谱序列为\(Z_j(t)=\xi_j\cos(t\lambda_j)+\eta_j\sin(t\lambda_j)\),其自协方差函数为
\[\gamma_{j-s}=\sigma_j^2\cos[(t-s)\lambda_j].
\]
三阶自协方差矩阵为
\[\Gamma_3=\sigma_j^2\begin{bmatrix}
1 & \cos \lambda_j & \cos 2\lambda_j \\
\cos\lambda_j & 1 & \cos\lambda_j \\
\cos 2\lambda_j & \cos \lambda_j & 1
\end{bmatrix},\\
\det(\Gamma_3)=(1-\cos^22\lambda_j)-2\cos\lambda_j(\cos\lambda_j-\cos\lambda_j\cos2\lambda_j)=0.
\]
AR(p)模型
Wold系数的递推公式:\(\psi_0=1\),对于\(k\ge 1\),如果定义下标为负数时Wold系数为0,则\(\psi_k=\sum_{j=1}^p a_j\psi_{k-j}\)(即\(A(\mathscr B)\psi_k=0\))。
注意到Wold系数其实是\(A^{-1}(z)\)的泰勒级数,所以
\[\begin{aligned}
1=&A(z)A^{-1}(z)\\
=&-\sum_{j=0}^p a_jz^j\sum_{k=0}^\infty \psi_kz^k\\
=&-\sum_{k=0}^\infty\sum_{j=0}^pa_j\psi_{k-j}z^k.
\end{aligned}
\]
当\(k=0\)时,
\[\sum_{j=0}^pa_j\psi_{-j}=-1\Rightarrow \psi_0=1,
\]
当\(k\ge 1\)时,
\[\sum_{j=0}^pa_j\psi_{k-j}=0\Rightarrow \psi_k=\sum_{j=1}^p a_j\psi_{k-j}.
\]
\({\rm AR}(p)\)序列自协方差函数的结构:\(A(\mathscr B)\gamma_k=\sigma^2\psi_{-k}\)。
对于\(k\ge 0\),由Yule-Walker方程直接得到\(A(\mathscr B)\gamma_k=0(k>0)\),\(A(\mathscr B)\gamma_k=\sigma^2\)。
对于\(k<0\),有
\[\begin{aligned}
&\quad \gamma_k-(a_1\gamma_{k-1}+\cdots+a_p\gamma_{k-p})\\
&=\mathbb{E}\left[X_{t-k}\left(X_t-\sum_{j=1}^p a_jX_{t-j} \right) \right]\\
&=\mathbb{E}(X_{t-k}\varepsilon_t)\\
&= \sigma^2\psi_{-k}.
\end{aligned}
\]
定理4.1:如果实数\(\gamma_k,k=0,\cdots,n\)使得\(\Gamma_{n+1}\)正定,则由其定义的Yule-Walker系数满足最小相位条件。
零均值平稳序列\(\{X_t\}\)是\({\rm AR}(p)\)序列的充要条件是,它的偏相关系数\(a_{n,n}\)在\(p\)后截尾。
充分性:记\(\boldsymbol{a}_p=(a_{p,1},\cdots,a_{p,p})=(a_1,\cdots,a_p)\),由Levinson递推公式和\(a_{p+k,p+k}=0\)得到,
\[a_{p+1,j}=a_{p,j}-a_{p+1,p+1}a_{p,p+1-j}=a_{p,j},\quad 1\le j\le p,\\
a_{p+k,j}=a_{p+k-1,j}=\cdots=a_{p,j}=a_j,\quad k\le 2,1\le j\le p,\\
a_{p+k,j}=a_{j,j}=0,\quad p<j\le p+k.
\]
进而对\(n\ge p\)总有\((a_{n,1},\cdots,a_{n,n})'=(a_1,\cdots,a_p,0,\cdots,0)\)。由Yule-Walker方程,对\(k\ge 1\)有
\[\gamma_k=\sum_{j=1}^p a_j\gamma_{k-j}.
\]
从这里开始的证明过程很具有代表性,务必掌握。
定义
\[\varepsilon_t=X_{t}-\sum_{j=1}^p a_jX_{t-j},\quad t\in\mathbb{Z},
\]
则\(\{\varepsilon_t\}\)是线性滤波,因而是平稳序列,且是零均值的,方差定义为\(\mathbb{D}(\varepsilon_t)=\sigma^2_p>0\)。下证其为白噪声,对\(t>s\),
\[\begin{aligned}
\mathbb{E}(\varepsilon_tX_s)=&\mathbb{E}\left[X_s\left(X_t- \sum_{j=1}^pX_{t-j} \right)\right]\\
=&\gamma_{t-s}-\sum_{j=1}^p\gamma_{t-s-j}\\
=&0,\\
\mathbb{E}(\varepsilon_t\varepsilon_s)=&\mathbb{E}\left[\varepsilon_t\left(X_s-\sum_{j=1}^pX_{s-j} \right) \right]\\
=&\mathbb{E}(\varepsilon_tX_s)-\sum_{j=1}^p\mathbb{E}(\varepsilon_tX_{s-j})\\
=&0.
\end{aligned}
\]
这就证明了\(\{\varepsilon_t\}\sim {\rm WN}(0,\sigma_p^2)\)。由定理4.1,\(a_1,\cdots,a_j\)满足最小相位条件,所以
\[X_t=\sum_{j=1}^p a_jX_{t-j}+\varepsilon_t,
\]
\(\{X_t\}\)是一个\({\rm AR}(p)\)序列。
必要性:对\({\rm AR}(p)\)序列\(X_t=\sum_{j=1}^p X_{t-j}+\varepsilon_t\),解Yule-Walker方程,得到
\[\begin{bmatrix}
\gamma_0 & \gamma_1 & \cdots & \gamma_p & \cdots & \gamma_{n-1} \\
\gamma_1 & \gamma_0 & \cdots & \gamma_{p-1} & \cdots & \gamma_{n-2} \\
\vdots & \vdots & & \vdots & & \vdots \\
\gamma_{n-1} & \gamma_{n-2} & \cdots &\gamma_{n-p-1} & \cdots & \gamma_{0}
\end{bmatrix}\begin{bmatrix}
a_{n,1} \\ a_{n,2} \\ \vdots \\ a_{n,n}
\end{bmatrix}=\begin{bmatrix}
\gamma_1 \\ \gamma_2 \\ \vdots \\ \gamma_n
\end{bmatrix}.
\]
记方程右端向量为\(\boldsymbol{\gamma}_n\),系数矩阵列向量分别为\(\boldsymbol{\beta}_1,\cdots,\boldsymbol{\beta}_n\)。由于\(k\ge 1\)时有
\[A(\mathscr B)\gamma_k=0,
\]
所以
\[\boldsymbol{\gamma}_n=\sum_{j=1}^p a_j\boldsymbol{\beta}_j.
\]
由Cramer法则,\(a_{n,p+1}=\cdots=a_{n,n}=0\),所以其偏相关系数是\(p\)后截尾的。
逆相关函数:\({\rm AR}(q)\)模型\(X_t=\sum_{j=1}^p a_jX_{t-j}+\varepsilon_t\)的逆相关函数是
\[\gamma_y(k)=\frac{1}{\sigma^2}\sum_{j=0}^{p-k}a_ja_{j+k},\quad 0\le k\le p,a_0=-1.
\]
否则\(\gamma_y(k)=0\)。
\[f_X(\lambda)=\frac{\sigma^2}{2\pi|A(e^{{\rm i}\lambda})|^2},\quad f_Y(\lambda)=\frac{1}{4\pi^2f_X(\lambda)}=\frac{|A(e^{{\rm i}\lambda})|^2}{2\pi\sigma^2}.
\]
这是\({\rm MA}(p)\)序列:\(X_t=A(\mathscr B)\epsilon_t\),\(\{\epsilon_t\}\sim {\rm WN}(0,\sigma^{-2})\)的谱密度,所以其逆相关函数为
\[\gamma_y(k)=\frac{1}{\sigma^2}\sum_{j=0}^{p-k}a_ja_{j+k},\quad 0\le k\le p.
\]
MA(q)模型
引理1.2:设实常数\(\{c_j\}\)使得\(c_{q}\ne 0\)和
\[g(\lambda)=\frac{1}{2\pi}\sum_{j=-q}^qc_je^{-{\rm i}j\lambda}\ge 0,\quad \lambda\in[-\pi,\pi],
\]
则有唯一的实系数多项式
\[B(z)=1+\sum_{j=1}^q b_jz^j\ne 0,\quad |z|<1,b_q\ne0,
\]
使得\(g(\lambda)=(\sigma_0^2/2\pi)|B(e^{{\rm i}\lambda})|^2\),这里\(\sigma_0^2\)是某个正常数。
零均值平稳序列\(\{X_t\}\)是\({\rm MA}(q)\)序列的充要条件是,其自协方差函数\(q\)后截尾。
必要性是显然的,下证充分性。当自协方差函数\(q\)后截尾时,由谱密度反演公式,\(\{X_t\}\)的谱密度为
\[f(\lambda)=\frac{1}{2\pi}\sum_{k=-q}^q\gamma_ke^{-{\rm i}k\lambda}.
\]
由引理1.2知,存在唯一的\(q\)阶\(B(z)\),使得
\[f(\lambda)=\frac{\sigma^2}{2\pi}|B(e^{{\rm i}\lambda})|^2.
\]
假定\(f(\lambda)\)恒正,对\(|z|\le 1\),有\(B(z)\ne 0\),定义平稳序列
\[\varepsilon_t=B^{-1}(\mathscr B)X_t=\sum_{j=0}^\infty h_jX_{t-j},
\]
由于\(B^{-1}(z)\)在\(|z|\le 1\)内解析,所以\(\{h_j\}\)绝对可和,故\(\mathbb{E}(\varepsilon_t)=0\)。为验证它是一个白噪声,求其谱密度,为
\[f_\varepsilon(\lambda)=f(\lambda)\frac{1}{|B(e^{{\rm i}\lambda})|^2}=\frac{\sigma^2}{2\pi},
\]
这就证明了\(\{\varepsilon_t\}\sim {\rm WN}(0,\sigma^2)\)。又因为
\[X_t=B(\mathscr B)B^{-1}(\mathscr B)X_t=B(\mathscr B)\varepsilon_t,
\]
所以\(\{X_t\}\)是一个\({\rm MA}(q)\)序列。
MA(1)的偏相关系数不截尾,并且可以求出。
上面已经证明过了,在这里再写一次。设\({\rm MA}(1)\)序列满足
\[X_t=\varepsilon_t+b\varepsilon_{t-1},\quad |b|<1.
\]
假定\(\{\varepsilon_t\}\sim {\rm WN}(0,1)\),则
\[\gamma_0=1+b^2,\quad \gamma_1=b,
\]
所以其\(n\)阶自协方差矩阵为
\[\Gamma_n=\begin{bmatrix}
1+b^2 & b & 0 & \cdots & 0 \\
b & 1+b^2 & b & \cdots & 0\\
0 & b & 1+b^2 & \cdots & 0\\
\vdots &\vdots & \vdots & & \vdots \\
0 & 0 & 0 & \cdots & 1+b^2
\end{bmatrix}
\]
定义
\[\mathcal B_n=\frac{1-b^{2(n+1)}}{1-b^2}=1+b^2+b^4+\cdots+b^{2n}.
\]
令\(\Gamma_n\)的行列式为\(d_n\),有\(d_1=1+b^2\),\(d_2=1+b^2+b^4\),
\[d_n=(1+b^2)d_{n-1}-b^2d_{n-2}.
\]
接下来使用数学归纳法能有效减少计算量。
如果\(d_n=\mathcal B_n\)对\(k< n\)都成立,则
\[\begin{aligned}
d_{n}=&(1+b^2)d_{n-1}-b^2d_{n-2}\\
=&(1+b^2)\mathcal B_{n-1}-b^2\mathcal B_{n-2}\\
=&1+b^2+\cdots+b^{2n-2}+b^2+b^4+\cdots+b^{2n}-(b^2+b^4+\cdots+b^{2n-2})\\
=&1+b^2+b^4+\cdots+b^{2n}\\
=&\mathcal B_n.
\end{aligned}
\]
所以结论得证,由Cramer法则,
\[a_{n,n}=\frac{-(-1)^nb\cdot b^{n-1}}{\mathcal B_n}=\frac{-(-b)^n(1-b^2)}{1-b^{2n+2}}.
\]
ARMA(p, q)模型
Wold系数的递推公式:\({\rm ARMA}(p,q)\)序列的Wold系数可以被递推,如果规定\(j>q\)时\(b_j=0\),\(k<0\)时\(\psi_k=0\),则
\[\psi_j=\left\{\begin{array}l
1,& j=0,\\
b_j+\sum_{k=1}^p a_k\psi_{j-k},&j>0.
\end{array}\right.
\]
类似\({\rm AR}(p)\)序列,
\[\begin{aligned}
A(z)\Phi(z)=&-\sum_{k=0}^p a_kz^k\sum_{j=0}^\infty \psi_jz^j \\
=& -\sum_{j=0}^\infty \sum_{k=0}^p a_k\psi_{j-k}z^j.
\end{aligned}
\]
而
\[A(\mathscr B)\Phi(z)\varepsilon_t=A(\mathscr B)X_t=\sum_{j=0}^q b_j\varepsilon_{t-j},
\]
所以
\[A(z)\Phi(z)=-\sum_{j=0}^\infty \sum_{k=0}^pa_k\psi_{j-k}z^j=\sum_{j=0}^pb_jz^j=\sum_{j=0}^\infty b_jz^j.
\]
当\(j=0\)时,
\[\psi_0=b_0=1,
\]
当\(j\ge 1\)时,
\[\psi_j=\sum_{k=1}^pa_k\psi_{j-k}+b_j.
\]
\({\rm ARMA}(p,q)\)序列的自协方差函数满足差分方程:
\[\gamma_k-\sum_{j=1}^pa_j\gamma_{k-j}=\left\{\begin{array}l
\sigma^2\sum_{j=k}^q b_j\psi_{j-k},& k<q; \\
\sigma^2b_q,& k=q;\\
0,& k>q.
\end{array}\right.
\]
对\(k<0\)定义\(\psi_k=0\),补充定义\(b_0=1\),由于
\[X_t=\sum_{j=1}^pa_jX_{t-1}+\sum_{j=0}^q b_j\varepsilon_{t-j},
\]
在方程两边同时乘以\(X_{t-k}\)后取期望,得到
\[\begin{aligned}
\gamma_k=&\mathbb{E}(X_tX_{t-k})\\
=&\mathbb{E}\left[\left(\sum_{j=1}^pa_jX_{t-j}+\sum_{j=0}^qb_j\varepsilon_{t-j} \right)X_{t-k} \right]\\
=&\sum_{j=1}^p a_j\gamma_{j-k}+\mathbb{E}\left(\sum_{j=0}^qb_j\varepsilon_{t-j}\sum_{l=0}^\infty\psi_l\varepsilon_{t-k-l} \right)\\
=&\sum_{j=1}^pa_j\gamma_{j-k}+\sigma^2\sum_{j=0}^q b_j\psi_{j-k},\quad k\in\mathbb{Z}.
\end{aligned}
\]
这就得到了上述差分方程。
引理2.2:设\(\{X_t\}\)是\({\rm ARMA}(p,q)\)模型\(A(\mathscr B)X_t=B(\mathscr B)\varepsilon_t\)的平稳解,如果又有白噪声\(\{\eta_t\}\)和实系数多项式\(C(\mathscr B)\)、\(D(\mathscr B)\)使得
\[C(\mathscr B)X_t=D(\mathscr B)\eta_t,\quad t\in\mathbb{Z},
\]
则\(C(z)\)的阶数\(\ge p\),\(D(z)\)的阶数\(\ge q\)。
\({\rm ARMA}(p, q)\)序列延拓的自协方差矩阵,如果阶数\(m\ge q\),则是可逆的。
\[\Gamma_{m,q}=\begin{bmatrix}
\gamma_q & \gamma_{q-1} & \cdots & \gamma_{q-m+1} \\
\gamma_{q+1} & \gamma_q & \cdots & \gamma_{q-m+2} \\
\vdots & \vdots & & \vdots \\
\gamma_{q+m} & \gamma_{q+m-1} & \cdots & \gamma_q
\end{bmatrix}.
\]
这个证明较难,主要运用的是\({\rm ARMA}(p,q)\)序列当\(k>q\)后\(\gamma_k\)的递推公式。
用反证法,如果\(|\Gamma_{m,q}|=0\),则存在\(\boldsymbol{\beta}=(\beta_0,\cdots,\beta_{m-1})'\ne 0\),使得\(\Gamma_{m,q}\boldsymbol{\beta}=0\),即
\[\sum_{l=0}^{m-1}\beta_l\gamma_{q+k-l}=0,\quad k=0,1,\cdots,m-1.
\]
由\({\rm ARMA}(p,q)\)满足的差分方程,有
\[\sum_{l=0}^{m-1}\beta_l\gamma_{q+m-l}=\sum_{l=0}^{m-1}\beta_l\sum_{k=1}^pa_k\gamma_{q+m-l-k}=\sum_{k=1}^pa_k\sum_{l=0}^{m-1}\beta_l\gamma_{q+k-l-m}=0,
\]
依次类推,可以得到
\[\sum_{l=0}^{m-1}\beta_l\gamma_{q+k-l}=0,\quad \forall k\ge 0.
\]
令
\[Y_t=\sum_{l=0}^{m-1}\beta_lX_{t-l},
\]
则\(\{Y_t\}\)是零均值平稳序列,又因为
\[\mathbb{E}(Y_tX_{t-q-k})=\sum_{l=0}^{m-1}\beta_l\gamma_{q+k-l}=0,\forall k\ge 0; \\
\mathbb{E}(Y_tY_{t-q-k})=\sum_{l=0}^{m-1}\beta_l\mathbb{E}(Y_{t}X_{t-q-k-l})=0,\forall k\ge 0.
\]
这说明\(\{Y_t\}\)的自协方差函数是\(q-1\)后截尾的,是一个\({\rm MA}(q)\)序列,存在\(\alpha_0,\cdots,\alpha_{q-1}\),使得
\[\sum_{l=0}^{m-1}\beta_lX_{t-l}=\sum_{j=0}^{q-1}\alpha_j\varepsilon_{t-j}.
\]
这里\(\{\varepsilon_t\}\sim {\rm WN}(0,\sigma^2)\),与引理2.2矛盾。
\({\rm ARMA}(p,q)\)序列的不可再约性:如果零均值平稳序列\(\{X_t\}\)有自协方差函数\(\{\gamma_k\}\),又设存在实数\(a_1,\cdots,a_p\),\(a_p\ne 0\)使得\(A(z)=1-\sum_{j=1}^p a_jz^j\)满足最小相位条件,且
\[\gamma_k-\sum_{j=1}^pa_j\gamma_{k-j}=\left\{\begin{array}l
c\ne 0,& k=q, \\
0,& k>q.
\end{array}\right.
\]
则\(\{X_t\}\)又是一个\({\rm ARMA}(p',q')\)序列,其中\(p'\le p,q'\le q\)。
此定理表明,如果给定了自协方差函数的结构信息,\({\rm ARMA}(p,q)\)的阶数信息就是可推断的。
同时这个定理的启示是,一旦出现关于自协方差结构的信息,就构造差项序列,它必定是一个白噪声或滑动平均序列。
\[\mathbb{E}(Y_tX_{t-k})=\mathbb{E}\left[\left(X_t-\sum_{j=1}^p a_jX_{t-j} \right)X_{t-k} \right]=\gamma_k-\sum_{j=1}^p a_j\gamma_{k-j}=\left\{\begin{array}l
c,& k=q;\\
0,& k>q.
\end{array}\right. \\
\mathbb{E}(Y_tY_{t-k})=\mathbb{E}\left[Y_t\left(X_{t-k}-\sum_{j=1}^pa_jX_{t-k-j} \right) \right]=\left\{\begin{array}l
c,& k=q; \\
0,& k>q.
\end{array}\right.
\]
所以\(\{Y_t\}\)是一个\({\rm MA}(q)\)序列,存在实系数多项式\(B(z)\)使得
\[A(\mathscr B)X_t=B(\mathscr B)Y_t,
\]
如果\(A(z)\)和\(B(z)\)有公共根,则有公因子\(C(z)\),用\(C^{-1}(\mathscr B)\)分别左乘上述模型,即可得到一个更低阶的\({\rm ARMA}(p',q')\)模型。
等阶\({\rm ARMA}(p,p)\)序列:设\(X_t\)是\({\rm AR}(p)\)序列,\(\{\varepsilon_t\}\sim {\rm WN}(0,\sigma^2)\)满足
\[X_t=\sum_{j=1}^pa_jX_{t-j}+\varepsilon_t,\quad t\in\mathbb{Z},
\]
又设\(\{\eta\}\)是和\(\{\varepsilon_t\}\)独立的\({\rm WN}(0,a^2)\),则\(Y_t=X_t+\eta_t\)是一个\({\rm ARMA}(p,p)\)序列。
本题意义主要在于,给出一个谱密度的应用场景。
由于\(Y_t=X_t+\eta_t\),所以
\[\begin{aligned}
Y_t=&\sum_{j=1}^p a_jX_{t-j}+\varepsilon_t+\eta_t \\
=&\sum_{j=1}^pa_jY_{t-j}+\varepsilon_t+\eta_t-\sum_{j=1}^p a_j\eta_{t-j}.
\end{aligned}
\]
定义\(Z_t=A(\mathscr B)Y_t\),则
\[Z_t=\varepsilon_t+\eta_t-\sum_{j=1}^pa_j\eta_{t-j},\\
\]
当\(k>q\)时,
\[\mathbb{E}(Z_tZ_{t-k})=0,\\
\mathbb{E}(Z_tZ_{t-q})=-a_pa^2\ne 0,
\]
所以\(\{Z_t\}\)是一个\({\rm MA}(q)\)序列,\(\{Y_t\}\)是一个\({\rm ARMA}(p',q')\)序列,这里\(p'\le p,q'\le p\)。因为\(Y_t=A^{-1}(\mathscr B)Z_t\),设\(\{Z_t\}\)的谱密度为\(f_Z(\lambda)\),则
\[\begin{aligned}
f_Z(\lambda)&=f_\varepsilon(\lambda)+|A(e^{{\rm i}\lambda})|^2f_\eta(\lambda)\\
&=\frac{\sigma^2}{2\pi}+\frac{a^2}{2\pi}|A(e^{{\rm i}\lambda})|^2,\\
f_Y(\lambda)&=\frac{f_Z(\lambda)}{|A(e^{{\rm i}\lambda})|^2}\\
&=\frac{a^2}{2\pi}+\frac{\sigma^2}{2\pi|A(e^{{\rm i}\lambda})|^2}\\
&=\frac{a^2|A(e^{{\rm i}\lambda})|^2+\sigma^2}{2\pi|A(e^{{\rm i}\lambda})|^2}\\
&\xlongequal{def}\frac{a^2}{2\pi}\left|\frac{B(e^{{\rm i}\lambda})}{A(e^{{\rm i}\lambda})} \right|^2.
\end{aligned}
\]
这表明\(A(z)\)和\(B(z)\)无公共根,所以\(\{Y_t\}\)是一个\({\rm ARMA}(p,p)\)序列。
参数估计
如果\(\gamma_k\to 0\),则样本均值是均值的相合估计量,并且是均方相合估计。
\[\begin{aligned}
\mathbb{E}(\bar X-\mu)^2&=\mathbb{E}\left[\frac{1}{N}\sum_{k=1}^N(X_k-\mu) \right]^2\\
&=\frac{1}{N^2}\sum_{j=1}^N\sum_{k=1}^N\gamma_{j-k}\\
&=\frac{1}{N^2}\sum_{k=-N+1}^{N-1}(N-|k|)\gamma_k\\
&\le \frac{1}{N}\sum_{k=-N}^N|\gamma_k|\to 0.
\end{aligned}
\]
如果定义自协方差函数的估计为
\[\hat\gamma_k=\frac{1}{N}\sum_{j=1}^{N-k}(x_j-\bar x_N)(x_{j+k}-\bar x_N),
\]
则自协方差矩阵的估计\(\hat \Gamma_n\)是任意阶正定的。
只要\(x_1,x_2,\cdots,x_N\)不全相同,则\(y_i=x_i-\bar x_N\)不全为0,故\(N\times(2N-1)\)型矩阵
\[A=\begin{bmatrix}
0 & \cdots & 0 & y_1 & y_2 & \cdots & y_{N-1} & y_N \\
0 & \cdots & y_1 & y_2 & y_3 & \cdots & y_N & 0 \\
\vdots & & \vdots & \vdots & \vdots & & \vdots & \vdots \\
y_1 & \cdots & y_{N-1} & y_N & 0 & \cdots & 0 & 0
\end{bmatrix}
\]
是满秩,而
\[\hat \Gamma_N=\frac{1}{N}AA',
\]
是正定矩阵,所以其任意阶主子式是正定矩阵。
如果\(k\to \infty\)时\(\gamma_k\to 0\),则对每个确定的\(k\),\(\hat \gamma_k\)是\(\gamma_k\)的渐进无偏估计。
设\(\mu=\mathbb{E}(X_1)\),则\(\{Y_t\}=\{X_t-\mu\}\)是零均值平稳序列,且\(\bar Y_N=\bar X_N-\mu\)。由于平移后的样本自协方差函数不发生变化,所以
\[\begin{aligned}
\hat\gamma_k&=\frac{1}{N}\sum_{j=1}^{N-k}(Y_j-\bar Y_N)(Y_{j+k}-\bar Y_N)\\
&=\frac{1}{N}\sum_{j=1}^{N-k}[Y_jY_{j+k}-\bar Y_N(Y_j+Y_{j+k})+\bar Y_N^2]\\
\end{aligned}
\]
注意到
\[\mathbb{E}(\bar Y_N^2)\to 0,\\
\mathbb{E}[\bar Y_N(Y_j+Y_{j+k})]\le \sqrt{\mathbb{E}(\bar Y_N^2)\mathbb{E}(Y_{j+k}+Y_j)^2}\le \sqrt{4\mathbb{E}(\bar Y_N^2)\gamma_0}\to 0.
\]
所以
\[\mathbb{E}(\hat\gamma_k)=\frac{1}{N}\sum_{j=1}^{N-k}\mathbb{E}(Y_jY_{j+k})+o(1)=\frac{N-k}{N}\gamma_k+o(1)\to \gamma_k.
\]
中心极限定理的应用:设\(\{\varepsilon_t\}\)是独立同分布的\({\rm WN}(0,\sigma^2)\),\(a\in(-1,1)\),如果
\[X_t=aX_{t-1}+\varepsilon_t,
\]
求\(\mu_n,\sigma_n\),使得
\[\frac{\exp(\bar X_n)-\mu_n}{\sigma_n}\stackrel {d}\to N(0,1).
\]
本题的主要意义在于,给出一个中心极限定理的应用场景,尽管不是课本上所提到的那种中心极限定理。
只需求分布函数即可,
\[\begin{aligned}
&\quad \mathbb{P}\left(\frac{\exp(\bar X_n)-\mu_n}{\sigma_n}\le x \right)\\
&=\mathbb{P}\left[\bar X_n\le \ln(\sigma_nx+\mu_n) \right]\\
&=\mathbb{P}\left[\frac{X_1+X_2+\cdots+X_n}{n}\le \ln(\mu_n+x\sigma_n) \right]\\
&= \mathbb{P}\left[\frac{a(X_0-X_n)+\varepsilon_1+\cdots+\varepsilon_n}{(1-a)n}\le \ln(\mu_n+x\sigma_n) \right]\\
&=\mathbb{P}\left[\frac{\varepsilon_1+\cdots+\varepsilon_n}{\sqrt{n}}\le\sqrt{n}(1-a)\ln(\mu_n+x\sigma_n)-\frac{a(X_0-X_n)}{\sqrt{n}}\right]\\
&=\mathbb{P}\left[\frac{\sum_{j=1}^n \varepsilon_j}{\sigma\sqrt{n}}\le\frac{\sqrt{n}(1-a)\ln(\mu_n+x\sigma_n)}{\sigma}-\frac{a(X_0-X_n)}{\sigma\sqrt{n}} \right]\\
&\approx\Phi\left(\frac{n(1-a)\ln(\mu_n+x\sigma_n)-a(X_0-X_n)}{\sigma \sqrt{n}} \right).
\end{aligned}
\]
希望
\[\frac{n(1-a)\ln(\mu_n+x\sigma_n)-a(X_0-X_n)}{\sigma \sqrt{n}}\approx x,
\]
即
\[\frac{\sqrt{n}(1-a)}{\sigma}\ln(\mu_n+x\sigma_n)\approx x,
\]
必有\(\mu_n=1\)(以便等价无穷小替换),同时
\[\sigma_n=\frac{\sigma}{\sqrt{n}(1-a)}.
\]
线性预测
预测方程:如果\(\boldsymbol{a}\in\mathbb{R}^n\),使得\(\Gamma_x\boldsymbol{a}=\mathbb{E}(\boldsymbol{X}Y)\),则\(L(Y|\boldsymbol{X})=\boldsymbol{a}'\boldsymbol {X}\)。
对任何\(\boldsymbol{b}\in\mathbb{R}^n\),有
\[\begin{aligned}
\mathbb{E}(Y-\boldsymbol{b}'\boldsymbol{X})^2&=\mathbb{E}[Y-\boldsymbol{a}'\boldsymbol{X}+(\boldsymbol{a}-\boldsymbol{b})'\boldsymbol{X}]^2\\
&=\mathbb{E}(Y-\boldsymbol{a}'\boldsymbol{X})^2+\mathbb{E}[(\boldsymbol a-\boldsymbol b)'\boldsymbol X]^2+2\mathbb{E}[(Y-\boldsymbol a'\boldsymbol X)(\boldsymbol a-\boldsymbol b)'\boldsymbol X]\\
&=\mathbb{E}(Y-\boldsymbol a'\boldsymbol X)^2+\mathbb{E}[(\boldsymbol a-\boldsymbol b)'\boldsymbol X]^2+2(\boldsymbol a-\boldsymbol b)'\mathbb{E}[\boldsymbol X(Y-\boldsymbol a'\boldsymbol X)]\\
&=\mathbb{E}(Y-\boldsymbol a'\boldsymbol X)^2+\mathbb{E}[(\boldsymbol a-\boldsymbol b)'\boldsymbol X]^2\\
&\ge \mathbb{E}(Y-\boldsymbol a'\boldsymbol X)'.
\end{aligned}
\]
证毕。
预测误差是逐步递增的,但有上界;纯非决定性平稳序列随着预测间隔增大将均方收敛于\(0\)。
由于
\[\sigma_{k,m}^2=\mathbb{E}[X_{n+k}-L(X_{n+k}|X_n,X_{n-1},\cdots,X_{n-m+1})]^2,\\
\begin{aligned}
\sigma_k^2&=\lim_{m\to \infty}\sigma_{k,m}^2\\
&=\lim_{m\to \infty}\mathbb{E}[X_{k}-L(X_{k}|X_0,\cdots,X_{-m+1})]^2\\
&=\lim_{m\to \infty}\mathbb{E}[X_{k-1}-L(X_{k-1}|X_{-1},\cdots,X_{-m})]^2\\
&\ge\lim_{m\to \infty}\mathbb{E}[X_{k-1}-L(X_{k-1}|X_0,\cdots,X_{-m})]^2\\
&=\sigma_{k-1}^2.
\end{aligned}
\]
这说明预测误差随步长单调递增,但是
\[\sigma_{k}^2=\lim_{m\to \infty}\mathbb{E}[X_k-L(X_k|X_0,\cdots,X_{-m+1})]^2\le \lim_{m\to \infty}\mathbb{E}(X_k)^2=\gamma_0.
\]
对于纯非决定性平稳序列,随着预测间隔增大将均方收敛于0,即
\[\quad \lim_{k\to \infty}\lim_{m\to \infty}\mathbb{E}[L(X_{n+k}|X_n,X_{n-1},\cdots,X_{n-m+1})]^2.
\]
设\(\hat X_{n+k}=L(X_{n+k}|X_n,\cdots,X_{n-m+1})\),则由勾股定理,
\[\mathbb{E}(X_{n+k}^2)=\mathbb{E}(X_{n+k}-\hat X_{n+k})^2+\mathbb{E}(\hat X_{n+k}^2),
\]
当\(k\to \infty\)时,
\[\lim_{k\to \infty}\mathbb{E}(X_{n+k}^2)=\lim_{k\to \infty}\mathbb{E}(X_{n+k}-\hat X_{n+k})^2=\gamma_0,
\]
所以
\[\lim_{k\to \infty}\mathbb{E}(\hat X_{n+k}^2)=0.
\]
定理2.4:设\(\boldsymbol{X}_{n,m}=(X_n,X_{n-1},\cdots,x_{n-m+1})'\),对于\(Y\in L^2\),当\(m\to \infty\)时,
\[L(Y|\boldsymbol{X}_{n,m})\stackrel{\text{m.s.}}\to \hat Y=L(Y|H_n).
\]
这里\(H_n=\overline{\text{sp}}(X_n,X_{n-1},\cdots)\)。
这个定理的意义是理论上的,表示可以有穷历史预测无穷历史。
远期预报的均方误差:设\(\{X_t\}\)是非决定性平稳序列,则
\[\begin{aligned}
L(X_{t+n}|H_t)&=L(U_{t+n}|H_t)+L(V_{t+n}|H_t) \\
&=L\left(\sum_{j=0}^\infty a_j\varepsilon_{t-j}\bigg|H_t \right)+V_{t+n}\\
&=\sum_{j=n}^\infty a_j\varepsilon_{t+n-j}+V_n
\end{aligned}
\]
所以
\[\mathbb{E}[X_{t+n}-L(X_{t+n}|H_n)]^2=\mathbb{E}\left(\sum_{j=0}^{n-1}a_j\varepsilon_{t+n-j}\right)=\sigma^2\sum_{j=0}^{n-1}a_j^2.
\]
当\(n\to \infty\)时,预报的均方误差趋近于\(\mathbb{E}(U_t^2)\)。
有穷历史预测中,误差的张成空间与原序列的张成空间相同。
设\(\{Y_t\}\)是方差有限的零均值时间序列,对任何正整数,令\(\boldsymbol{Y}_n=(Y_1,\cdots,Y_n)'\),\(L_n=\overline{\text{sp}}(\boldsymbol{Y}_n)\)。其最佳线性预测为
\[\hat Y_1=0,\quad \hat Y_n=L(Y_n|\boldsymbol{Y}_{n-1}),\quad n=1,2,\cdots
\]
引入预测误差及其方差为
\[W_n=Y_n-\hat Y_n,\quad \nu_{n-1}=\mathbb{E}(W_n^2),
\]
再令\(\boldsymbol{W}_n=(W_1,\cdots, W_n)'\),\(M_n=\overline{\text{sp}}(W_1,\cdots,W_n)\),则欲证明\(\forall n,L_n=W_n\)。
对于\(n=1\),由于\(\hat Y_1=0\),所以\(W_1=Y_1\),即\(L_1=W_1\)。假设此结论对\(k\le n-1\)都成立,则当\(k=n\)时,
\[W_n=Y_n-L(Y_n|\boldsymbol{Y}_{n-1})\in L_n,\\
Y_n=W_n+\hat Y_{n}\in M_n.
\]
这是因为\(L(Y|\boldsymbol{Y}_{n-1})\in L_{n-1}\),\(\hat Y_n\in L_{n-1}=M_{n-1}\)。这就说明\(L_n=M_n\)。
平稳序列的递推预测:设\(\{X_n\}\)是零均值平稳序列,其自协方差函数为\(\{\gamma_k\}\),设
\[\boldsymbol{X}_n=(X_1,\cdots,X_n)',\quad Z_n=X_n-\hat X_n,
\]
则当\(\Gamma_n\)正定时,有
\[\hat X_{n+1}\xlongequal{def}L(X_{n+1}|\boldsymbol{X}_n)=\sum_{j=1}^n\theta_{n,j}Z_{n+1-j}.
\]
这里递推预测系数\(\{\theta_{n,j}\}\)和预测的均方误差\(\nu_n=\mathbb{E}(Z_{n+1}^2)\)满足如下的递推公式:
\[\nu_0=\gamma_0,\\
\theta_{n,n}=\frac{\gamma_n}{\nu_0}=\rho_n,\\
\theta_{n,n-k}=\frac{\gamma_{n-k}-\sum_{j=0}^{k-1}\theta_{k,k-j}\theta_{n,n-j}\nu_j}{\nu_k},\quad 0<k\le n-1,\\
\nu_n=\gamma_0-\sum_{j=0}^{n-1}\theta_{n,n-j}^2\nu_j.
\]
最好掌握证明,省得记忆。
由于\(\boldsymbol{X}_n\)的张成空间与\(\boldsymbol{Z}_n\)的张成空间相同,所以预测在形式上是成立的。所以对于\(0\le k\le n-1\),
\[\begin{aligned}
\mathbb{E}(\hat X_{n+1}Z_{k+1})&=\mathbb{E}\left[Z_{k+1}\left(\sum_{j=1}^{n}\theta_{n,n+1-j}Z_j \right) \right]\\
&=\sum_{j=1}^n\theta_{n,n+1-j}\mathbb{E}(Z_{k+1}Z_j)\\
&=\theta_{n,n-k}\nu_{k}.
\end{aligned}
\]
注意到
\[\hat X_{k+1}=\sum_{j=1}^k\theta_{k,j}Z_{k+1-j}=\sum_{j=0}^{k-1}\theta_{k,k-j}Z_{j+1},\\
\mathbb{E}(X_{n+1}Z_{k+1})=\mathbb{E}(\hat X_{n+1}Z_{k+1}),
\]
所以
\[\begin{aligned}
\theta_{n,n-k}&=\frac{\mathbb{E}(\hat X_{n+1}Z_{k+1})}{\nu_k}\\
&=\frac{\mathbb{E}(X_{n+1}Z_{k+1})}{\nu_k}\\
&=\frac{\mathbb{E}[X_{n+1}(X_{k+1}-\sum_{j=1}^{k}\theta_{k,k+1-j}Z_{j})]}{\nu_k}\\
&=\frac{\gamma_{n-k}-\sum_{j=1}^k\theta_{k,k+1-j}\mathbb{E}(X_{n+1}Z_j)}{\nu_k}\\
&=\frac{\gamma_{n-k}-\sum_{j=1}^k\theta_{k,k+1-j}\mathbb{E}(\hat X_{n+1}Z_j)}{\nu_k}\\
&=\frac{\gamma_{n-k}-\sum_{j=1}^k\theta_{k,k+1-j}\theta_{n,n+1-j}\nu_{j-1}}{\nu_k}\\
&=\frac{\gamma_{n-k}-\sum_{j=0}^{k-1}\theta_{k,k-j}\theta_{n,n-j}\nu_{j}}{\nu_k}.
\end{aligned}
\]
对于预测的均方误差,有
\[\nu_n=\mathbb{E}(Z_{n+1}^2)=\mathbb{E}(X_{n+1}^2-\hat X_{n+1}^2)=\gamma_0-\sum_{j=1}^n\theta_{n,n-j}^2\nu_j.
\]
可以用它递推一两项以作自测。
\({\rm MA}(q)\)序列的递推预测只需要最后\(q\)个新息。
设\({\rm MA}(q)\)序列的逐步预测误差是\(\{\hat\varepsilon_n\}\)(即样本新息,\(\hat \varepsilon_n=X_{n}-L(X_n|\boldsymbol{X}_{n-1})\)),则
\[L(X_{n+1}|\boldsymbol{X}_n)=L(X_{n+1}|X_n,\cdots,X_{n-q+1})=L(X_{n+1}|\hat\varepsilon_n,\cdots,\hat\varepsilon_{n-q+1}).
\]
也就是
\[L(X_{n+1})=\sum_{j=1}^q\theta_{n,1}\hat\varepsilon_{n+1-j}.
\]
从而
\[\nu_n=\gamma_0-\sum_{j=1}^q\theta_{n,1}^2\nu_{n-j}.
\]
如果是远期预测,则
\[L(X_{n+k+1}|\boldsymbol{X}_n)=\sum_{j=k+1}^q\theta_{n+k,j}\hat\varepsilon_{n+k+1-j},\quad 1\le k\le q-1.
\]
这是因为当我们知道\({\rm MA}(q)\)模型的系数时,所有递推系数和预测均方误差已经可递推计算,只有\(\hat\varepsilon_{t}\)是依赖于观测值计算的。
\({\rm ARMA}(p,q)\)序列的递推预测
对于\({\rm ARMA}(p,q)\)模型序列\(\{X_t\}\),构造辅助数列:
\[Y_t=\left\{\begin{array}l
X_t/\sigma,& t=1,2,\cdots,m, \\
A(\mathscr B)X_t/\sigma,& t>m.
\end{array}\right.\quad m=\max\{p,q\}.
\]
显然\(Y_t\in\overline{\text{sp}}(X_1,\cdots,X_t)\),且对于\(t>m\),\(X_t=\sigma Y_t+\sum_{j=1}^p a_pX_{t-j}\),由数学归纳法可知\(X_t\)、\(Y_t\)的张成空间相同,进而它们的样本新息张成空间也相同。设\(W_t=Y_t-\hat Y_t\),\(Z_t=X_t-\hat X_t\),总有(省略证明)
\[Z_t=\sigma W_t,\quad \mathbb{E}Z_t^2=\sigma^2\mathbb{E}W_t^2,
\]
令\(\theta_{n,j}\)是\(\{Y_t\}\)的预测递推系数,则对于\(1\le n\le m\),此时\(\{Y_t\}\)还是平稳的,就有
\[\hat Y_{n+1}=\sum_{j=1}^n\theta_{n,j}W_{n+1-j},
\]
于是
\[\hat X_{n+1}=\sigma\hat Y_{n+1}=\sum_{j=1}^n\theta_{n,j}\sigma W_{n+1-j}=\sum_{j=1}^n\theta_{n,j}Z_{n+1-j},\quad l\le n\le m.
\]
对于\(n>m\),
\[\hat Y_{n+1}=\sum_{j=1}^q \theta_{n,j}W_{n+1-j},\\
\hat X_{n+1}=\sigma\hat Y_{n+1}+\sum_{j=1}^p a_jX_{n+1-j}=\sum_{j=1}^pa_jX_{n+1-j}+\sum_{j=1}^q\theta_{n,j}Z_{n+1-j},\quad n>m.
\]
注意,这里\(\theta_{n,j}\)是\(\{Y_t\}\)的递推预测系数(而不是\(\{X_t\}\)的),因此要利用非平稳序列的系数递推预测与预测误差递推,稍微麻烦。
远期预测的无效性:设\(\{X_t\}\)是可逆的\({\rm ARMA}(p,q)\)序列,
\[\hat X_{n+k}\xlongequal{def}L(X_{n+k}|X_n,X_{n-1},\cdots,X_1),\quad k\ge 1.
\]
则有
\[\lim_{k\to \infty}\lim_{n\to \infty}\mathbb{E}(\hat X_{n+k}^2)=0,\\
\lim_{n\to \infty}\mathbb{E}(\hat X_{n+1}-X_{n+1})^2=\sigma^2.
\]
由\(\{X_t\}\)的平稳性,有
\[\hat X_{n+k}\xlongequal{def}L(X_{n+k}|X_n,\cdots,X_1)=L(X_k|X_0,\cdots,X_{-n+1}).
\]
所以
\[\lim_{n\to \infty}\hat X_{n+k}=L(X_k|H_0)=L(X_k|M_0).
\]
由\(X_k\)的Wold展开,有
\[\begin{aligned}
&\quad L(X_k|\varepsilon_0,\varepsilon_{-1},\cdots)\\
&=L\left(\sum_{j=0}^{\infty}a_j\varepsilon_{k-j}\bigg|\varepsilon_0,\varepsilon_{-1},\cdots \right)\\
&=\sum_{j=0}^{k-1} a_j\varepsilon_{t-j}.
\end{aligned}
\]
所以
\[\lim_{k\to \infty}\lim_{n\to \infty}\mathbb{E}(\hat X_{n+k}^2)=\sigma^2\sum_{j=0}^{k-1} a_j^2=0.
\]
同时,也有
\[\lim_{n\to \infty}\mathbb{E}[(X_{n+1}-\hat X_{n+1})^2]=\varepsilon_1.
\]
对可逆的\({\rm ARMA}(p,q)\)序列,预测的均方误差收敛于白噪声方差。
\[\begin{aligned}
&\quad \lim_{k\to \infty}\nu_k\\
&=\lim_{k\to \infty}\mathbb{E}(X_{k+1}-\hat X_{k+1})^2\\
&=\lim_{k\to \infty}\mathbb{E}(X_1-L(X_1|X_0,\cdots,X_k))^2\\
&=\mathbb{E}(\varepsilon_1^2) \\
&=\sigma^2.
\end{aligned}
\]
特别当\(\sigma^2=1\)时,有
\[\lim_{N\to \infty}\frac{1}{N}\ln(\nu_0\nu_1\cdots\nu_{N-1})=0.
\]
此即\({\rm ARMA}(p,q)\)的极大似然估计中用到的结论。





