计量经济学复习笔记(七):推翻经典假设
本章中,我们将给出OLS估计量\(\hat\beta\)是BLUE的证明,并且说明经典假设对BLUE性具有什么样的影响。在此之前,要回顾经典假设的内容。
- 回归模型是正确设定的。
- 解释变量\(X_1,X_2,\cdots,X_k\)在所抽取的样本中具有变异性,且不存在严格线性相关性。
- 随机干扰项是条件零均值的。
- 随机干扰项是条件同方差的。
- 随机干扰项不序列相关。
在此基础上,得到OLS估计量为
它是最小方差线性无偏估计。注意,这里没有要求各随机误差项服从正态分布。
1、BLUE性的证明
为发挥经典假设的作用,要从\(\hat\beta\)的来源说起。我们在第四篇笔记中已经得到了\(\hat\beta\)的表达式,具体说来,它是使得残差平方和最小的\(\beta\)值。
至此,我们得到一个等式:
要从中解出\(\hat\beta\),需要用到一个性质:\(X'X\)是可逆的,这就要求\(X\)不存在严格的多重共线性。此时
这就说明\(\hat\beta\)是线性的。接下来验证其无偏性,计算其期望:
如果要使得\(\mathbb{E}(\hat\beta)\)是无偏的,则要求\(\mathbb{E}(\mu)=0\),这用到了随机干扰项的条件零均值性。
为了验证其有效性,先计算其方差,为
如果随机干扰项满足条件同方差性,就有\(\mathbb{D}(\mu)=\sigma^2I_n\),此时
可以看出,只有当随机干扰项的同方差性与序列不相关性被满足,\(\hat\beta\)的方差才具有如此简洁的形式,否则接下来对方差的讨论就没有意义。并且可以看出,如果\(X\)具有近似的多重共线性,\(X'X\)的某些特征值就会接近0,求逆后其对角线元素就会很大,导致\(\mathbb{D}(\hat\beta)\)的对角线元素——各个\(\beta_i\)的方差很大,使得估计的精度变小;不仅如此,放大的区间估计还容易导致\(0\)落入置信区间,从而导致解释变量被错误排除在外。
接下来,在满足条件同方差性和序列不相关性的前提(即\(\mathbb{D}(\mu)=\sigma^2I_n\))下,证明\(\hat\beta\)的有效性,这一性质也被表述为高斯-马尔科夫定理。假设还有其他线性无偏估计量,不妨记作
则由无偏性得到
这里又用到了\(\mu\)的条件零均值性。由于\(\beta\)是未知的,所以\(DX=O\)。此时
注意到星号步骤运用了\(\mathbb{D}(\mu)=\sigma^2I_n\)。由自协方差矩阵的非负定性,有\(\mathbb{D}(\hat\beta^*)\ge \mathbb{D}(\hat\beta)\),这就证明了\(\hat\beta\)是有效的。可以看出,关于随机误差项的假设在\(\hat\beta\)的得出,以及BLUE性的证明上具有重要作用。如果这些假设不成立,会怎样呢?
2、放宽经典假设
不幸的是,在实际模型中,有些假设是不成立的。书上列举了一些违背基本假定的情形:
- 解释变量之间存在严重多重共线性。
- 随机干扰项序列存在异方差性。
- 解释变量具有内生性。
- 模型有设定偏误。
- 随机干扰项具有序列相关性。
由于我们回顾了\(\hat\beta\)的来源以及BLUE性的证明,以下讨论也变得比较简单。接下来的内容大多是课本内容的提炼,可作复习用。
多重共线性
多重共线性定义:对于模型
如果某两个或多个解释变量之间出现相关性,则称为存在多重共线性。具体还可以分为完全共线性与近似共线性。
- 如果某一个变量能完全由其他解释变量线性表示,则称为存在完全共线性,此时\(r(X)<k+1\)。
- 如果存在\(c_1X_{i1}+c_2X_{i2}+\cdots+c_kX_{ik}+\upsilon_i=0\),其中\(c_i\)不全为0,\(\upsilon_i\)为随机干扰项,则称为存在近似共线性。
如果是完全共线性的,则\(r(X'X)<k+1\),不可逆,也就不存在参数估计量;如果近似共线性,则\((X'X)^{-1}\)的对角线元素将会很大,也就增大了各个模型系数\(\beta_i\)的方差,使得变量的显著性检验、模型的预测功能失去意义。
要检验多重共线性是否存在,即检验多重共线性由哪些变量引起,这里介绍一种方法:判定系数检验法。
对每一个解释变量\(X_j\),用其他的解释变量对它作回归,计算相应的拟合优度(此时称为判定系数)\(R_j^2\)。如果\(X_j\)的判定系数\(R_j^2\)很大,说明其他解释变量可以很好地线性表示这个解释变量,自然存在多重共线性,与之关联的一个统计量称为“方差膨胀因子(VIF)”,其计算方式是
显然,\({\rm VIF}_j\)越大,\(R_j^2\)越大,所以可以用VIF来评判某个变量的多重共线性效果。如果要给出一个严格的判定标准,可以对每一个回归方程作\(F\)检验,即构造如下的参数统计量:
异方差性
异方差性定义:对于不同的样本点\((X_{i1},\cdots,X_{ik},Y_i)\),随机干扰项方差不再是常数,而是互不相同的\(\sigma_i^2\)。
如果存在异方差性,则\(\mathbb{D}(\mu)\)退化成一个普通的对角矩阵(而不是单位阵),这就导致\(\mathbb{D}(\hat\beta)\)没有很好的表达形式,同时,有效性的证明中\((*)\)处等号不能被满足,从而失去有效性。失去有效性,还会导致变量的显著性显著失去意义(因为估计的\(\mathbb{D}(\hat\beta)\ne\sigma^2(X'X)^{-1}\),实际应用时用\(\hat\sigma^2\)代替),模型的预测功能失效。
异方差性的检验有BP检验和White检验两种,它们的思想都是将模型的随机干扰项的平方视为解释变量的函数,不同的是BP检验只考虑了线性函数,而White检验追加考虑了二次函数。具体操作为:
-
对原模型:\(Y_i=\beta_0+\beta_1X_{i1}+\beta_2X_{i2}+\cdots+\beta_kX_{ik}+\mu_i\)使用OLS回归,计算残差项\(e_i\)。
-
构造辅助线性回归:\(e_i^2=f(X_{i1},\cdots,X_{ik})+\varepsilon_i\),这里BP检验与White检验具有不同的形式:
\[\text{B-P检验:}f=\delta_0+\delta_1X_{i1}+\delta_2X_{i2}+\cdots+\delta_kX_{ik},\\ \text{White检验:}f=\delta_0+\sum_{t=1}^k\delta_tX_{it}+\sum_{j,l=1}^k\delta_{jl}X_{ij}X_{il}. \] -
计算得到辅助线性回归的系数矩阵,计算回归判定系数\(R_{e^2}^2\)。
-
构造假设检验,对不同的检验有不同的假设检验形式:
\[\text{B-P检验:}H_0:\delta_1=\delta_2=\cdots=\delta_k=0,\\ \text{White检验:}H_0:\delta_1=\cdots=\delta_k=\delta_{11}=\cdots=\delta_{kk}=0. \] -
构造检验\(F\)统计量或拉格朗日统计量\(LM=nR_{e^2}^2\)。
异方差性可以用加权最小二乘(WLS)或异方差稳健标准误法,其中异方差稳健标准误法,指的是用OLS估计得到的\(e_i^2\),作为相应\(\sigma_i^2\)的代表,再计算\(\mathbb{D}(\hat\beta)\)。此时,称
为\(\hat\beta_i\)的异方差稳健标准误。
内生解释变量
内生解释变量定义:如果随机干扰项的条件零均值假设不成立,则称为内生解释变量,或解释变量具有内生性。如果存在一个或多个随机变量是内生解释变量,则称原模型存在内生解释变量问题。现假设模型为\(Y_i=\beta_0+\beta_1X_{i1}+\beta_2X_{i2}+\cdots+\beta_kX_{ik}+\mu_i\),其中\(X_2\)是内生解释变量。
- 同期无关但异期相关:\(\mathbb{E}(X_{i2}\mu_i)=0\),但对于\(s\ne 0\),\(\mathbb{E}(X_{i2}\mu_{i-s})\ne 0\)。
- 同期相关:\(\mathbb{E}(X_{i2}\mu_i)\ne 0\),这是截面数据模型中,内生性的主要表现。
内生解释变量导致\(\mathbb{E}(\mu)\ne 0\),因此参数估计量不是无偏估计量,从而也不是一致的。如果无偏性得不到保证,也不用进一步讨论最小方差线性无偏估计了,因此内生解释变量导致的问题,比近似共线性、异方差性导致的问题还大。
我们希望,即使有效性得不到满足,至少参数估计量是无偏的,或者再退而求其次,是渐进无偏且相合的,这样,样本量足够大时,依然能精准地估计参数。
按照教材所说,工具变量法是最常用的,能得到大样本下的一致估计量的方法。此时,我们需要寻找到一个变量\(Z\),它与所替代的随机解释变量\(X_2\)高度相关,却与随机干扰项不相关,最好还和模型中的其他解释变量不高度相关(避免出现严重的共线性),即
用\(Z\)代替\(X_2\)后得到的工具变量矩阵(依然记作\(Z\),注意区分)为
原有系数矩阵依然记作\(Z\),则按照工具变量法得到的参数估计量为
在小样本下,\(\tilde \beta\)是有偏估计,但在大样本下是相合的。
如果关于一个内生变量\(X_2\)找到了多个工具变量\(Z_1,Z_2\),则可以使用两阶段最小二乘法(2SLS)。假设原有的方程是\(Y_i=\beta_0+\beta_1X_{i}+\beta_2Z_i+\mu_i\)其步骤是:
-
第一阶段,用\(Z_1\)、\(Z_2\)以及原有的外生变量\(Z\)来拟合\(X\),得到第一阶段回归方程:
\[\hat X_{i}=\hat a_0+\hat a_1Z_{i1}+\hat a_2Z_{i2}+\hat a_3Z_i. \] -
第二阶段,用第一阶段得到的\(\hat X_i\)代替\(X_i\),得到第二阶段回归方程:
\[Y_i=\beta_0+\beta_1\hat X_{i2}+\beta_2Z_i+\mu_i\\ \Downarrow \\ \hat Y_i=\hat\beta_0+\hat\beta_1\hat X_i+\hat\beta_2Z_i. \]
内生性检验:使用Hausman检验,对于线性回归模型\(Y_i=\beta_0+\beta_1X_i+\beta_2Z_{i1}+\mu_i\),如果明确知道\(Z_1\)已知,但怀疑\(X\)是同期内生的,则豪斯曼检验的步骤为:
-
寻找一个外生变量\(Z_2\)作为工具变量,将怀疑是内生变量的\(X\),关于\(Z_1,Z_2\)作OLS估计:
\[X_i=\alpha_0+\alpha_1Z_{i1}+\alpha_2Z_{i2}+\upsilon_i. \]得到残差项\(\hat\upsilon_i\)。
-
将残差项加入原模型,进行OLS估计:
\[Y_i=\beta_0+\beta_1X_{i}+\beta_2Z_{i1}+\delta\hat\upsilon_i+\varepsilon_t. \] -
检验假设\(H_0:\delta=0\),如果认为\(\delta=0\),就认为\(X\)是同期外生变量;否则认为\(X\)是同期内生变量。
模型设定偏误
模型设定偏误的分类:一类是关于解释变量选取的偏误(遗漏相关变量,误选无关变量),另一类是关于模型函数形式选取的偏误(错误函数形式)。
遗漏相关变量的后果:
- 导致OLS估计量在小样本下有偏,大样本下不一致。
- 如果遗漏变量\(X_2\)与考虑的变量\(X_1\)无关,则\(X_1\)的模型参数估计量无偏且一致,但是截距项会有偏且不一致。
- 随机干扰项的方差估计也是有偏的。
- 不管遗漏变量\(X_2\)与\(X_1\)关系如何,模型参数估计量的方差估计都是有偏的(这里指偏离正确模型参数估计的方差)。
包含无关变量的后果:
- 仍然是无偏且一致的,但往往是无效的,即方差会偏大。
- 随机干扰项的方差能被正确估计。
错误函数形式的后果:全方位后果。
序列相关性
序列相关性主要出自时间序列模型,指的是模型的随机干扰项不再是相互独立的。这种序列相关性可能产生于经济变量的固有惯性、模型的设定偏误、数据的“编造”(其实是生成),并且往往都是存在的。
由我们之前的讨论,序列相关性也会导致\(\mathbb{D}(\mu)\)不再是单位矩阵,并且甚至不再是对角矩阵,因此也会导致参数估计量失去有效性,模型的检验和预测功能失去意义。
序列相关性的检验:使用DW检验,它假定
- 解释变量\(X\)非随机
- 随机干扰项\(\mu\)是一阶自回归的(\(\mu_t=\rho\mu_{t-1}+\varepsilon_t\))
- 回归模型中不包含滞后被解释变量
- 回归模型含有截距项
在此基础上,检验假设\(H_0:\rho=0\),如果\(H_0\)成立,就不存在一阶自回归。为了执行假设,构造DW统计量为
如果\({\rm DW}\)统计量在2附近,就认为模型不存在一阶自相关,具体的相关情况需要考虑两个临界值\(d_L,d_U\),根据\({\rm DW}\)的值来判断相关情况:
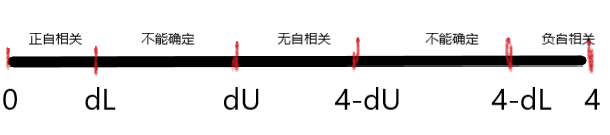
至此,本系列的计量经济学学习笔记就完结了。本系列笔记的重点在于第二、三章的线性回归模型部分,包含了许多在实际应用中并不必要的数理推导,但这对结论的理解、记忆很有帮助,感兴趣的读者可以自行尝试。此外,对于第四章之后的内容,由于考试要求较低,在我们的笔记中提及得也极为简略,如果想进一步学习,需要参考更多教材。
接下来如果有时间,可能会出一篇关于概念解释的笔记。

