计量经济学复习笔记（二）：一元线性回归(下)

回顾上文，我们通过OLS推导出了一元线性回归的两个参数估计，得到了以下重要结论：

\[\hat\beta_1=\frac{\sum x_iy_i}{\sum x_i^2},\quad \hat\beta_0=\bar Y-\hat\beta_1\bar X. \]

注意总体回归模型是\(Y=\beta_0+\beta_1X+\mu\)，同时我们还假定了\(\mu\sim N(0,\sigma^2)\)，这使得整个模型都具有正态性。这种正态性意味着许多，我们能用数理统计的知识得到点估计的优良性质，完成区间估计、假设检验等，本文就来详细讨论上述内容。

1、BLUE

我们选择OLS估计量作为一元线性回归的参数估计量，最主要的原因就是它是最小方差线性无偏估计(Best Linear Unbiased Estimator)，这意味着它们是：

1. 线性的。
2. 无偏的。
3. 最小方差的。

不过，光给你这三个词，你可能会对定义有所困扰——比如，关于什么线性？又关于什么是无偏的？我们接下来就对OLS估计量的BLUE性详细讨论，包括简单证明。原本我认为，证明在后面再给出会更合适，引入也更顺畅，但是我们接下来要讨论的许多，都有赖于OLS估计量的BLUE性，因此我还是决定将这部分内容放在这里。

首先是线性性，它指的是关于观测值\(Y_i\)线性，这有什么意义呢？注意到，在之前的讨论中，我们总讨论在给定\(X\)的取值状况下的其他信息，如\(\mu\)的条件期望、方差协方差等，因此我们往往会在这部分的讨论中将\(X\)视为常数（而不是随机变量）看待，这会带来一些好处。而因为\(\mu\sim N(0,\sigma^2)\)且\(\mu_i\)是从\(\mu\)中抽取的简单随机样本，且\(\mu_i\)与\(X_i\)无关，所以由正态分布的性质，有

\[Y_i|X_i\sim N(\beta_0+\beta_1X_i,\sigma^2). \]

实际上，由于参数真值\(\beta_1,\beta_1\)是常数，所以每一个\(Y_i\)在给定了\(X_i\)的水平下，都独立地由\(\mu_i\)完全决定，而\(\mu_i\)序列不相关（在正态分布的情况下独立），所以\(Y_i\)之间也相互独立。这样，如果有一个统计量是\(Y_i\)的线性组合，那么由正态分布的可加性，这个统计量就自然服从正态分布，从而我们可以很方便地对其进行参数估计、假设检验等。

所以现在我们来验证\(\hat\beta_0,\hat\beta_1\)是\(Y_i\)的线性组合，先从比较容易处理的\(\hat\beta_1\)开始，我们已经算出了

\[\hat\beta_1=\frac{\sum x_iy_i}{\sum x_i^2}, \]

为了在这个式子中出现\(Y_i\)，只要把\(y_i\)打开就行了，也就是

\[\hat\beta_1=\frac{\sum x_i(Y_i-\bar Y)}{\sum x_i^2}=\frac{\sum x_i Y_i-\bar Y\sum x_i}{\sum x_i^2}. \]

注意到\(\sum x_i=\sum(X_i-\bar X)=0\)，所以有

\[\hat\beta_1=\sum_{i=1}^n\frac{x_i}{\sum x_i^2}Y_i\xlongequal{def}\sum_{i=1}^nk_iY_i,\quad k_i=\frac{x_i}{\sum x_i^2}. \]

这就将\(\hat\beta_1\)表示成了\(Y_i\)的线性组合。同理对于\(\hat\beta_0\)，由于

\[\hat\beta_0=\bar Y-\bar X\hat \beta_1=\sum_{i=1}^n\frac{Y_i}n-\bar X\sum_{i=1}^nk_iY_i=\sum_{i=1}^n\left(\frac1n-\bar Xk_i \right)Y_i\xlongequal{def}\sum_{i=1}^nw_iY_i. \]

所以\(\hat\beta_0\)也是\(Y_i\)的线性组合。进一步地由于\(Y_i\)独立地服从正态分布，所以\(\hat\beta_1,\hat\beta_0\)也服从正态分布。

无偏性指的是\(\hat\beta_0,\hat\beta_1\)是\(\beta_0,\beta_1\)的无偏估计——理解概念，\(\beta_0\)与\(\beta_1\)是总体回归函数中的参数，在给定问题的情形下是一个待估参数，因此也是常数。我们已经验证了\(\hat\beta_0,\hat\beta_1\)都是独立正态分布\(Y_i\)的线性组合，因此它们的均值就很好求得，基于\(Y_i|X_i\sim N(\beta_0+\beta_1X_i,\sigma^2)\)的事实，有

\[\mathbb E(\hat\beta_1)=\sum_{i=1}^n\frac{x_i\mathbb E(Y_i)}{\sum x_i^2}=\sum_{i=1}^n\frac{x_i(\beta_0+\beta_1X_i)}{\sum x_i^2}=\frac{\beta_0\sum x_i}{\sum x_i^2}+\frac{\beta_1\sum x_iX_i}{\sum x_i^2},\\ \mathbb E(\hat\beta_0)=\sum_{i=1}^n\left(\frac1n-\frac{\bar Xx_i}{\sum x_i^2} \right)(\beta_0+\beta_1X_i)=\beta_0+\beta_1\bar X-\beta_1\bar X\frac{\sum x_iX_i}{\sum x_i^2}, \]

由于\(\sum x_iX_i=\sum x_i(x_i+\bar X)=\sum x_i^2+\bar X\sum x_i=\sum x_i^2\)且\(\sum x_i=0\)，所以

\[\mathbb E(\hat\beta_1)=\beta_1,\quad \mathbb E(\hat\beta_0)=\beta_0. \]

这里，我们得到了参数估计量\(\hat\beta_1,\hat\beta_0\)的均值，说明了它们是无偏估计。

最后最小方差性，指的是在所有线性无偏估计中，参数估计量\(\hat\beta_1,\hat\beta_0\)是方差最小的（注意线性无偏估计的限定条件）。为证明\(\hat\beta_1\)是最小方差的，我们可以另外构造一个线性无偏估计量，记作

\[\hat\beta_1^*=\sum_{i=1}^n(k_i+d_i)Y_i=\hat\beta_1+\sum_{i=1}^nd_iY_i, \]

无偏性要求使得

\[\mathbb E\left(\sum_{i=1}^n d_iY_i\right)=\sum_{i=1}^nd_i(\beta_0+\beta_1X_i)=0, \]

由\(\beta_0,\beta_1\)的未知性，我们必须保证\(\sum d_i=\sum d_iX_i=0\)，也就是\(\sum d_i(X_i-\bar X)=\sum d_ix_i=0\)。所以

\[\begin{aligned} \mathbb D(\hat\beta_1^*)=&\mathbb D\left(\hat\beta_1+\sum_{i=1}^nd_iY_i \right)\\ =&\mathbb D(\hat\beta_1)+\mathbb D\left(\sum_{i=1}^nd_iY_i \right)+2{\rm Cov}\left(\sum_{i=1}^nk_iY_i,\sum_{i=1}^nd_iY_i \right)\\ =&\mathbb D(\hat\beta_1)+\mathbb D\left(\sum_{i=1}^nd_iY_i \right)+2\sigma^2\sum_{i=1}^nk_id_i\\ =&\mathbb D(\hat\beta_1)+\mathbb D\left(\sum_{i=1}^nd_iY_i \right)+2\sigma^2\frac{\sum x_id_i}{\sum x_i^2}\\ =&\mathbb D(\hat\beta_1)+\mathbb D\left(\sum_{i=1}^nd_iY_i \right)+0\\ \ge& \mathbb D(\hat\beta_1). \end{aligned} \]

同理，为证明\(\hat\beta_0\)是最小方差的，同样构造一个\(\hat\beta_0^*=\sum(w_i+d_i)Y_i\)，无偏性要求也会使得\(\sum w_id_i=0\)，仿照\(\hat\beta_1\)的步骤就证明了\(\mathbb D(\hat\beta_0^*)\ge \mathbb D(\hat\beta)\)。

由线性性，我们还可以计算出参数估计量的方差，因为我们要用\(\hat\beta_1\)和\(\hat\beta_0\)估计真值\(\beta_1,\beta_0\)，既然它们是无偏的，它们的方差越小，估计结果就越接近我们想要的真值，因此计算它们的方差具有重要意义。

\[\begin{aligned} \mathbb D(\hat\beta_1)=&\sigma^2\sum k_i^2=\sigma^2\sum\frac{x_i^2}{(\sum x_i^2)^2}=\frac{\sigma^2}{\sum x_i^2}.\\ \mathbb D(\hat\beta_0)=&\sigma^2\sum w_i^2\\ =&\sigma^2\sum\left(\frac1n-\bar Xk_i \right)^2\\ =&\sigma^2\sum\left(\frac1{n^2}-\frac{2\bar Xk_i}{n}+\bar X^2k_i^2 \right)\\ =&\sigma^2\left(\frac1n+\frac{\bar X^2}{\sum x_i^2} \right)\\ =&\frac{\sum x_i^2+n\bar X^2}{n\sum x_i^2}\sigma^2\\ =&\frac{\sum X_i^2}{n\sum x_i^2}\sigma^2. \end{aligned} \]

它们的方差都随着分母——自变量的离差平方和的增大而增大，这表明我们的样本容量越大，估计值就会有越高的精度。

2、参数分布与区间估计

结合正态性假定，我们已经确定了参数估计量的均值、方差，就得到了其分布：

\[\hat\beta_1\sim N\left(\beta_1,\frac{\sigma^2}{\sum x_i^2} \right),\\ \hat\beta_0\sim N\left(\beta_0,\frac{\sum X_i^2}{n\sum x_i^2}\sigma^2 \right). \]

得到了参数分布以后，我们是不是就可以对参数值给出区间估计了呢？事实上，我们还缺一个关键的参数——随机误差方差\(\sigma^2\)，由于它是未知的，我们还是没法得知方差的具体值，也就不能得到参数的真实分布。因此，我们需要找到一个\(\sigma^2\)的无偏估计。

一个很自然的想法是，用残差项\(e\)作为\(\mu\)的估计，进而估计出\(\mu\)的唯一参数\(\sigma^2\)，因此先探究\(e\)的分布。由于

\[e_i=Y_i-(\hat\beta_0+\hat\beta_1X_i)=(\beta_0-\hat\beta_0)+(\beta_1-\hat\beta_1)X_i+\mu_i, \]

所以看起来\(e_i\)也是一系列正态分布的线性组合，但我们是否能得到\(e\)服从（条件）正态分布的结论？可以，但并不是直接\(\beta_0,\beta_1\)的直接加和，因为\(\beta_0\)和\(\beta_1\)的独立性还没有被验证，不要忘了，只有独立正态分布的线性组合才服从正态分布。我们依然可以把\(e_i\)看成独立正态分布的线性组合，因为\(\hat\beta_0,\hat\beta_1\)都是\(Y_i\)的线性组合，进一步是各个\(\mu_i\)的线性组合。

事实上，我们还缺少一些关键性的条件：\(\hat\beta_0\)与\(\hat\beta_1\)的协方差，还有\(\hat\beta_0,\hat\beta_1\)与\(\mu_i\)的协方差。我们可以稍作计算，得到

\[\begin{aligned} {\rm Cov}(\hat\beta_0,\hat\beta_1)=&{\rm Cov}\left(\sum_{i=1}^nw_iY_i,\sum_{i=1}^nk_iY_i \right)\\ =&\sigma^2\sum w_ik_i\\ =&\sigma^2\sum\left(\frac1n-\bar X k_i \right)k_i\\ =&-\sigma^2\bar X\sum k_i^2\\ =&-\frac{\sigma^2\bar X}{\sum x_i^2}.\\ {\rm Cov}(\hat\beta_1,\mu_i) =&k_i\sigma^2=\frac{x_i\sigma^2}{\sum x_i^2},\\ {\rm Cov}(\hat\beta_0,\mu_i) =&w_i\sigma^2=\left(\frac1n-\bar Xk_i \right)\sigma^2=\frac{\sum x_i^2-n\bar Xx_i}{n\sum x_i^2}\sigma^2. \end{aligned} \]

有了这些，我们已经可以计算\(e_i\)的分布，进而用单个\(e_i\)得到关于\(\sigma^2\)的估计，容易看出，由于均值项都被抵消，最后得到的\(e_i\)一定是零均值正态的。但只用一个残差是无法估计\(\sigma^2\)的，数理统计的知识告诉我们，为了充分利用样本信息，我们应该使用充分统计量作为估计量。容易知道，\(\boldsymbol e=(e_1,\cdots,e_n)\)服从多维正态分布，但各分量之间相互独立，因此可以用联合密度导出充分统计量。忽略推导细节，这里的充分统计量是\(\sum e_i^2\)，因此我们应该计算\(\sum e_i^2\)的分布，从而给出\(\sigma^2\)的估计量，事实上，可以证明

\[\frac{\sum e_i^2}{\sigma^2}\sim \chi^2(n-2). \]

证明过程与证明正态分布的样本方差服从卡方分布类似，对于计量经济学略显繁琐，如果需要，我将在后面补充这个命题的证明。现在我们知道了\(\sum e_i^2\)的分布，自然可以计算均值为\(\sigma^2(n-2)\)，所以我们往往会用如下估计量作为\(\sigma^2\)的无偏估计：

\[\hat\sigma^2=\frac{\sum e_i^2}{n-2},\quad \frac{(n-2)\hat\sigma^2}{\sigma^2}\sim \chi^2(n-2). \]

此时再来考虑\(\hat\beta_0,\hat\beta_1\)的参数估计问题就简单很多了，因为我们使用卡方统计量来替代方差真值，所以相应的区间估计应当基于\(t\)分布构造枢轴量。对于\(\hat\beta_1\)，有

\[\hat\beta_1\sim N\left(\beta_1,\frac{\sigma^2}{\sum x_i^2} \right)\\ \frac{\hat\beta_1-\beta_1}{\sqrt{\frac{\hat\sigma^2}{\sum x_i^2}}}=\frac{\frac{\hat\beta_1-\beta_1}{\sqrt{\sigma^2/\sum x_i^2}}}{\sqrt{\hat\sigma^2/\sigma^2}}\simeq\frac{U(0,1)}{\sqrt{\chi^2_{n-2}/(n-2)}}\sim t(n-2). \]

对于\(\hat\beta_0\)，类似的证明过程可以得出

\[\frac{\hat\beta_0-\beta_0}{\sqrt{\frac{\sum x_i^2-n\bar Xx_i}{n\sum x_i^2}\hat\sigma^2}}\sim t(n-2). \]

实际上，求\(\hat\beta_0,\hat\beta_1\)的参数估计与方差未知情形的正态分布均值估计有异曲同工之妙，只不过样本方差的获得方式不太一样。对于回归参数，我们只要推导出\(\hat\beta_0,\hat\beta_1\)的方差，再用残差平方和除以自由度\(n-2\)代替方差里的\(\sigma^2\)，就能得到枢轴量，剩下的过程与数理统计的情形一致。

3、参数的假设检验

在数理统计中，我们已经知道，对参数分布族的假设检验与求参数分布族的区间估计，在一定程度上是等价的。具体说来，如果我们已经求得参数\(\lambda\)的一个置信水平为\(1-\alpha\)的区间估计\([L,S]\)，那么对如下假设进行显著性水平为\(\alpha\)的双边检验：

\[\text{test: }H_0:\lambda=\lambda_0\leftrightarrow H_1:\lambda\ne\lambda_0, \]

只需要判断是否\(\lambda_0\in[L,S]\)即可，如果\(\lambda_0\in[L,S]\)，则接受\(H_0\)，否则就拒绝\(H_0\)。如果是单边假设检验，则相应的置信区间就变成同等置信水平的置信限。因此，在我们讨论完\(\hat\beta_0,\hat\beta_1\)的分布之后，实际上假设检验问题也讨论完了。

在计量经济学中，我们对单个参数的假设检验，最主要是用于判断变量是否显著的，也就是用\(X\)来预测\(Y\)是否有意义。具体说来，对于回归函数\(Y=\beta_0+\beta_1X+\mu\)，如果\(\beta_1=0\)，则我们不需要用\(X\)来预测\(Y\)，因为不论\(X\)是什么取值，都对\(Y\)没什么影响。也就是检验如下的假设：

\[H_0:\beta_1=0. \]

另一种假设检验，是检验是否\(X,Y\)之间存在完全的比例关系，也就是有没有\(Y=\beta_1X+\mu\)，检验的假设是

\[H_0:\beta_0=0. \]

如果只是单纯想要知道是否应该接受\(H_0\)，则假设检验与区间估计无异，但为了衡量接受原假设的信心有多大，或者拒绝原假设的信心有多大，我们都会计算检验的p-value。检验的p-value用通俗的语言解释，就是如果你这个原假设是成立的，那么出现比你的观测值更离谱的观测值的概率是多少，我们用p-value来表示这个概率，如果这个概率很小，就说明你这个观测值已经很难再离谱了，因此我们没有什么接受原假设的理由；如果这个概率很大，就说明你的观测值不离谱，完全可以接受原假设。

具体应用到回归系数的假设检验中，由于我们构造的枢轴量满足\(t\)分布，假设枢轴量的观测值是\(t_0\)，则由于\(t\)分布的对称性，用\(t_{\alpha}\)表示\(t\)分布的下\(\alpha\)分位数（\(\mathbb P(t<t_\alpha)=\alpha\)），则检验的p-value是

\[p_v=\mathbb 2P(t>|t_0|). \]

如果\(p_v\)很小，我们就应该拒绝\(\beta_i=0\)的原假设，认为回归系数很显著。

现在我们继续分析上文的案例。

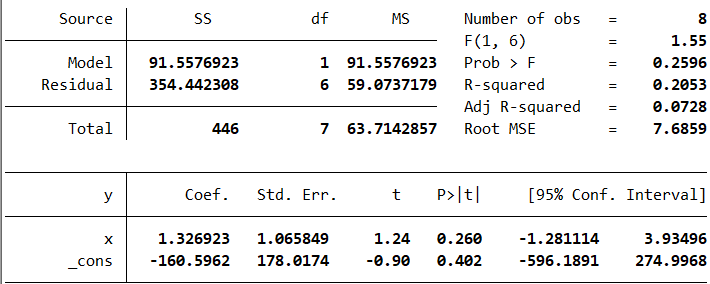
通过计算，我们得到的回归方程为

\[Y=1.3269X-160.5962, \]

计算残差，得到的残差分别是4.3077、-1.0192、1.6538、-6、-2.3269、-9.6538、14.0192、-0.9808，所以残差平方和为354.4404，方差的估计值是

\[\hat\sigma^2=\frac{354.4404}{8-2}=59.0734. \]

现在，我们可以了解回归结果中的部分剩余数值。

这里：

• Residual SS就是残差平方和(Residual Sum Square)，得到的结果与我们计算相差不多，这是因为我们在计算过程中忽略了部分误差。
• Residual MS则是残差均方误差，计算所得的就是随机误差方差的估计值。
• x和_cons后面的t指的是根据假设\(\beta_1=0\)和\(\beta_0=0\)构造枢轴量的观测值，后面的P>|t|就是检验的p-value，从这里可以看出p-value都大于0.05，所以在显著性水平为0.05的情况下不能拒绝等于0的原假设，认为斜率和截距都不存在。
• [95% Conf. Interval]指的是置信水平为95%的置信区间，因为这两个参数的置信区间都包含0，所以它们得出了与假设检验一致的结论。

---

本文我们对回归系数OLS估计量的分布作了进一步的讨论，得到了基础假设下回归系数OLS估计量的分布。同时，通过残差平方和引出了随机误差项方差的估计，进而完成了对参数的区间估计与假设检验。现在留给我们的问题，就剩下回归的效果了，我们应当如何判断回归的效果如何，又应该如何使用我们建立的回归模型？

这些问题，留待下文讨论。