计量经济学复习笔记（一）：一元线性回归(上)

在本文中，我们将对回归的基本概念作出解释，介绍相关分析与因果分析之间的差异；辨析总体回归函数、总体回归模型、样本回归函数、样本回归模型之间的关系，了解我们的工作是从样本推断总体，用样本回归函数来预测总体回归函数。最后，对回归中最简单的一元线性回归模型作出介绍，并给出参数估计的方法。

1、什么是回归

在数学上，回归指的是研究一组随机变量和另一组随机变量之间关系的统计方法，这句话包含的意义有两个。一是回归的研究主体是两组随机变量，在实际生活中，研究的对象往往来自于某个总体中的样本；我们知道，样本具有两重性，在观测之前是一个服从总体分布的随机变量，观测之后就是一个定值，因此我们的回归对象往往是一堆观测记录。二是回归揭示的是关系，这种关系可能是确定的函数关系，也可能是不确定的相关关系，且往往是不确定的；不论是哪种关系，回归总蕴含着某种“因果”，即一个变量的变化会是影响另一个变量变化的原因。

关于如何看待这样的因果关系，我们来作一个假设。现在我们得到了某个关系式：

\[Y=f(X)+\mu. \]

这里\(Y\)是一个随机变量，\(X\)是一个随机向量，\(f\)是已知且确定的随机向量函数，\(\mu\)是模型所包含的不可控误差。如果我们想让\(Y\)提升，如果因果关系成立，我们就会通过改变\(X\)的取值以增加\(f(X)\)的值，也就是说\(X\)是关系到\(Y\)变动的成因。但如果因果关系不成立，我们改变了\(X\)的值就不会对\(Y\)的值造成影响，而是推翻这个关系式。

典型的例子是夏季儿童溺死数与雪糕售卖数的关系，夏季儿童溺死数会与雪糕售卖数同步增加，但我们能不能为了减少儿童溺死数而控制雪糕的销量？显然是不可以的，如果我们强行减少了雪糕售卖数，儿童溺死数也不可能减少，这样的关系会被打破。

因此，为了使我们得到的模型不仅具有预测能力，还具有解释能力，我们都要求回归分析的变量之间存在一定的依赖关系。这时候，因变量\(Y\)又被称为被解释变量，自变量\(X\)被称为解释变量。

在\(Y\)与\(X\)之间存在的关系往往多种多样，这也导致回归函数是多种多样的，但由于我们不可能找到世界上所有的回归函数形式，我们只能找一些常用的函数类，通过改变它们的参数来达到合适的回归效果。常用的回归函数有线性回归、多项式回归、指数回归、对数回归、Logistic回归等，其中以线性回归的形式最为简单，因此我们从线性回归开始讨论起是合适的。

2、回归的基本概念

在第一节中，我们提到，回归的研究对象是某个总体，这个总体往往非常非常大，以至于我们只能从其中抽取样本进行研究，从样本推测总体性质。但是，由于我们希望获得的是能反映总体的变量间关系式，我们需要假定这样的关系式是存在的。

现在我们假设一个有一个总体，其中的每一个个体\(\omega\)都具有两个具有因果关系的属性\((Y,X)\)，这里\(X\)是\(Y\)的影响因素。我们想探究的是如何通过变化\(X\)来影响\(Y\)，自然要找到\(Y,X\)之间的一个回归关系，如果给定\(X\)，我们会认为\(Y\)的什么值最有可能出现？概率论知识告诉我们——条件期望就是给定\(X\)情况下的最佳预测，即

\[f(X)=\mathbb E(Y|X). \]

如果我们能找到每一个给定\(X\)水平下\(Y\)的条件期望，就找到了\(Y\)关于\(X\)的一个最佳联系式，我们称这样的\(f(X)\)为总体回归函数。由于随机性，每一个具有相同\(X\)水平的个体也不可能有同样的\(Y\)，因此，称

\[\mu=Y-\mathbb E(Y|X) \]

为观察值\(Y\)围绕其期望值的离差，也被称为随机误差项或随机干扰项。

但，由于总体往往大到无法遍历，我们自然不会知道总体的分布函数，也就求不了条件期望，即直接获得总体回归函数是不可能的。无法获得总体回归函数，自然也不可能得到\(\mu\)的观测值，因此离差\(\mu\)是一个不可观测的随机变量。习惯上，我们称\(\mathbb E(Y|X)\)是\(Y\)的系统性部分，\(\mu\)是\(Y\)的随机性部分，这就构成了总体回归模型：

\[Y=\mathbb E(Y|X)+\mu. \]

既然总体回归函数和误差都不可观测，我们就只能利用数理统计的知识，通过样本估计总体。通过从总体中抽取某些样本，观察它围绕在哪一个函数附近，这个函数就称作样本回归函数，记作

\[\hat Y=\hat f(X). \]

有没有发现这里的\(Y\)上面加上了一顶帽子？这表明，通过这个式子\(\hat f\)算出来的值并不是给定\(X\)后真正的\(Y\)值，而是通过样本观测得到的函数，近似认为给定\(X\)的情况下\(Y\)离这个值比较近而已。当然，不管多近，\(Y\)与\(\hat Y\)之间总有差距，这个差距\(\hat\mu=e=Y-\hat Y\)就称为残差，加上残差以后，就得到了样本回归模型：

\[Y=\hat f(X)+\hat \mu. \]

会不会感觉有点绕？其实只要区分以下六个概念就好了：

• 总体回归函数(population regression function)、总体回归模型(population regression model)、随机误差(stochastic error)；
• 样本回归函数(sample regression function)、样本回归模型(sample regression model)、残差(residual)。

如何区分呢？首先，区分总体与样本的关键，就在于这个东西是基于总体计算的还是基于样本计算的，由于总体不可观测，总体回归函数、总体回归模型只是“理论上”存在的，但我们不可能直接观测它是什么样的，而是只能通过样本估计总体，而基于样本计算出的，就是样本回归函数或样本回归模型了。其次，区分函数与模型，关键就在于随机误差/残差，即实际的总体往往不表现为确定的函数关系，不可能代入\(X\)就能得到精准的\(Y\)，回归模型中允许了这样的误差存在，而回归函数就是用于计算预测值的工具。

现在就留下了一个问题——如何通过抽取的样本来计算样本回归函数呢？直接凭感觉画一条线拟合，既主观又难以测量，而且不精准，所以我们需要基于数学推导，给出通过样本估计总体的方式。

3、一元线性回归模型

现在我们要转向样本回归函数(SRF)的计算上了。之前我们提到过，回归函数的形式多种多样，我们总要依赖于一些函数类，通过调整参数得到样本回归函数，而线性回归函数就是最简单的一种回归函数类。特别当我们只有一个被解释变量\(Y\)和一个解释变量\(X\)的情况下，SRF是一元线性回归函数，对应的回归模型是一元线性回归模型。一元线性回归模型总可以用这样的形式表示：

\[Y=\beta_0+\beta_1X+\mu. \]

注意，这是总体回归模型，也就是说我们假定总体满足\(\mathbb E(Y|X)=\beta_0+\beta_1X\)，这样处理的好处就是，我们从茫然地估计总体，简化成了估计两个待估参数\(\beta_0,\beta_1\)，问题得到大大简化。

对参数进行点估计就成了数理统计中的问题，但如果不对模型加以约束，我们就不知道有关于分布的任何信息，从而无从下手。这里，我们暂时搁置对一元线性回归的基本假设问题，我们将在多元线性回归中详细讨论它，所以现在我们只提出必要的、关于分布的假设。

假设从总体中抽取的总体为\((X_i,Y_i),i=1,\cdots,n\)，随机误差项为\(\mu_i\)，则我们一般不考虑\(X\)的分布信息，只作如下的要求：

1. \(\mathbb E(\mu_i|X)=0,\mathbb D(\mu_i|X)=\sigma^2\)，这表明在任何\(X\)的水平下，随机误差项都是一个零均值、同分布序列。这条性质也暗含了\(\mathbb E\mu_i=0,\mathbb D\mu_i=\sigma^2\)。
2. \({\rm Cov}(\mu_i,\mu_j|X)=0\)如果\(i\ne j\)，这表明在任何\(X\)的水平下，随机误差项序列不相关。这条性质也暗含了\({\rm Cov}(\mu_i,\mu_j)=0\)。
3. \({\rm Cov}(\mu_i,X)\)，这表明随机误差项与自变量不存在任何形式的相关性。
4. \(\mu_i|X\sim N(0,\sigma^2)\)，这表明在任何\(X\)的水平下，\(\mu_i\)都服从正态分布。

实际上，正态分布的要求是为了更好的区间估计而提出的，这也说明随机误差项总体\(\mu\sim N(0,\sigma^2)\)，每一次观测都可以视为从这个总体抽取独立同分布\(\text{(i.i.d.)}\)样本，因此，总体\(Y\)在给定\(X\)的情况下可以确定分布：

\[Y|X\sim N(\beta_0+\beta_1X,\sigma^2). \]

我们的任务依然是根据样本的情况估计参数，此时需要估计的参数就是\(\beta_0,\beta_1,\sigma^2\)，从而确定\(Y\)在给定\(X\)的水平时的分布。

4、一元线性回归模型参数估计

最典型的参数估计方法是普通最小二乘法(OLS)，我们也只介绍这种方法而不考虑矩法估计、极大似然估计。

最小二乘法的思想在高中就已经接触过，我们需要找到一个拟合函数，使得所有点到拟合函数的误差平方和尽可能小，利用微积分的方法可以很容易地得到这个拟合函数的形态。假设符合要求的拟合函数是

\[\hat Y=\hat\beta_0+\hat\beta_1X, \]

则点\(i\)到\(\hat Y_i\)的误差平方是

\[(Y_i-\hat Y_i)^2=[Y_i-(\hat\beta_0+\hat\beta_1X_i)]^2, \]

所有点的误差平方和就是

\[Q=\sum_{i=1}^n[Y_i-(\hat\beta_0+\hat\beta_1X_i)]^2. \]

我们的目标是找到一组参数\(\hat\beta_0,\hat\beta_1\)使得\(Q\)最小，由多元函数求极值的方法，只要让偏导数为零即可，也就是

\[\frac{\partial Q}{\partial\hat\beta_0}=\sum_{i=1}^n(-2)\cdot[Y_i-(\hat\beta_0+\hat\beta_1X_i)]=0,\\ \frac{\partial Q}{\partial \hat\beta_1}=\sum_{i=1}^n(-2X_i)\cdot[Y_i-(\hat\beta_0+\hat\beta_1X_i)]=0. \]

也就是

\[\begin{pmatrix} n & \sum\limits_{i=1}^nX_i\\ \sum\limits_{i=1}^nX_i & \sum\limits_{i=1}^nX_i^2 \end{pmatrix}\begin{pmatrix} \hat\beta_0 \\ \hat\beta_1 \end{pmatrix}=\begin{pmatrix} \sum\limits_{i=1}^n Y_i \\ \sum\limits_{i=1}^nX_iY_i \end{pmatrix}, \]

解得

\[\hat\beta_0=\frac{\sum\limits_{i=1}^nY_i\sum\limits_{i=1}^nX_i^2-\sum\limits_{i=1}^nX_i\sum\limits_{i=1}^nX_iY_i}{n\sum\limits_{i=1}^nX_i^2-\left(\sum\limits_{i=1}^nX_i \right)^2}, \hat\beta_1=\frac{n\sum\limits_{i=1}^nX_iY_i-\sum\limits_{i=1}^nX_i\sum\limits_{i=1}^nY_i}{n\sum\limits_{i=1}^nX_i^2-\left(\sum\limits_{i=1}^nX_i \right)^2}. \]

这个式子看起来十分麻烦，为了化简这个式子，引入中心化这个概念。以下记\(\bar X\)为\(X_i\)的样本均值，\(\bar Y\)为\(Y_i\)的样本均值，\(x_i=X_i-\bar X,y_i=Y_i-\bar Y\)，这样，\(\hat\beta_1\)可以被改写成

\[\begin{aligned} \hat\beta_1=&\frac{n\sum\limits_{i=1}^nX_iY_i-\sum\limits_{i=1}^nX_i\sum\limits_{i=1}^nY_i}{n\sum\limits_{i=1}^nX_i^2-\left(\sum\limits_{i=1}^nX_i \right)^2}\\ =&\frac{n\sum\limits_{i=1}^n(X_i-\bar X)(Y_i-\bar Y)+n^2\bar X\bar Y-n^2\bar X\bar Y}{n\sum\limits_{i=1}^n(X_i-\bar X)^2+n^2\bar X^2-n^2\bar X^2}\\ =&\frac{\sum\limits_{i=1}^nx_iy_i}{\sum\limits_{i=1}^n x_i^2}\xlongequal{def}\frac{\sum x_iy_i}{\sum x_i^2}. \end{aligned} \]

很神奇地，\(\hat\beta_1\)被简化了很多。而

\[Y_i=\hat\beta_0+\hat\beta_1X_i+e_i,\\ \sum_{i=1}^nY_i=n\hat\beta_0+\hat\beta_1\sum_{i=1}^nX_i+\sum_{i=1}^ne_i,\\ \Downarrow \\ n\bar Y=n\hat\beta_0+n\hat\beta_1\bar X+\sum_{i=1}^ne_i. \]

注意到\(\sum_{i=1}^n e_i=\sum_{i=1}^n[Y_i-(\hat\beta_0+\hat\beta_1X_i)]\)恰好是OLS过程中的第一个式子，所以

\[n\bar Y=n\hat\beta_0+n\hat\beta_1\bar X,\\ \hat\beta_0=\bar Y-\hat\beta_1\bar X. \]

这样我们就得到了运用中心化数据，求参数估计的简化方法。

由本节的推导内容，我们知道了如何由一系列数据建立回归方程，现在就举个例子试试。下表是中国某地区部分男性的身高体重数据，尝试建立线性回归模型。

	身高\(X_i\)(cm)	体重\(Y_i\)(kg)
1	163	60
2	164	56
3	165	60
4	167	55
5	168	60
6	169	54
7	170	79
8	170	64

第一步，求出身高和体重的均值：这里\(\bar X=167,\bar Y=61\)。

第二步，求出离差相关数据，并计算求和

	1	2	3	4	5	6	7	8	\(\sum\)
\((X_i-\bar X)^2\)	16	9	4	0	1	4	9	9	52
\((X_i-\bar X)(Y_i-\bar Y)\)	4	15	2	0	-1	-14	54	9	69

第三步，计算参数估计值，得到

\[\hat\beta_1=1.3269,\quad \hat\beta_0=-160.5923.\\ \hat Y=-160.5923+1.3269X. \]

通过软件验算，这是正确的回归结果（观察x和_cons的值）。

---

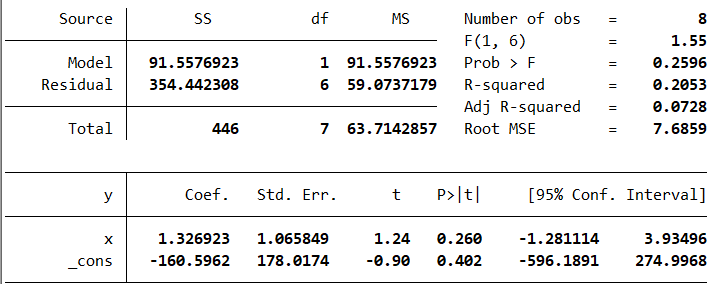
本文的内容就到此为止了，但是还有许多需要解决的问题，比如：我们需要估计的参数是三个——两个回归系数以及一个方差，但是方差应该如何估计呢？在我们的推导过程中，似乎没有用到随机误差项的正态假定，这个假定对我们的工作有什么贡献？软件计算给出的结果中，除了能够直接阅读的回归系数，其他参数又是什么意思？

在之后的学习中，我们将对这些问题一一作出回答。