排序算法总结

直接插入排序

 

1、将待排序的记录放入数组 arr[n] 中；

2、循环 n-1 次，使用顺序查找法，判断 arr[i] 在序列 arr[0]~arr[i-1] 中的位置，然后将 arr[i] 插入序列 arr[0]~arr[i] 中，得到 arr[0]~arr[i] 的有序序列，继续循环，最终得到长度为 n 的有序序列 arr[n]。

 

演示：

无序数组 p[] = {51, 22, 56, 81, 17, 23, 90, 16};  黄色标记位表示插入的位置。

 C++代码实现：

using namespace std;
void InsertSort(int l[], int n){
    for(int j,i=1; i<n; i++){
        if(l[i]<l[i-1]){
            int x = l[i];
            l[i] = l[i-1];
            for(j=i-2; j>=0&&x<l[j]; j--){
                l[j+1] = l[j];
            }
            l[j+1] = x;
        }
    }
    for(int i=0; i<n; i++){
        cout << l[i] <<" ";
    }
}
int main(){
    int p[] = {51, 22, 56, 81, 17, 23, 90, 16};
    InsertSort(p, 8);
    return 0;
}

时间复杂度为 O(N^2)，空间复杂度为O(1)；

算法评价：（1）稳定排序；

　　　　　（2）算法简便，且容易实现；

　　　　　（3）同时适用于链式查找结构，且在查找过程中不需要移动记录，只需修改相应指针；

　　　　　（4）更适用于初始记录有序（正序）的情况，当初始记录无序，且 N 较大时，此算法的时间复杂度较高，不宜采用。

 

---

折半插入排序

 

1、将待排序的记录放在数组 arr[n] 中；

2、循环 n-1 次，每次循环使用折半查找法，判断 arr[i] 在有序序列 a[0]~a[i-1] 中的位置，然后将 arr[i] 插入序列 arr[0]~arr[i] 中，得到 arr[0]~arr[i] 的有序序列，继续循环，最终得到长度为 n 的有序序列 arr[n]。

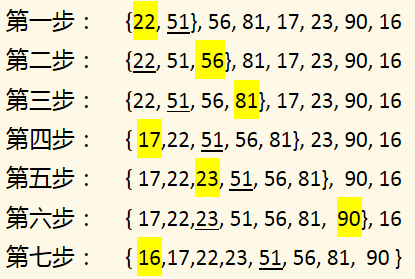
演示：无序数组 p[] = {51, 22, 56, 81, 17, 23, 90, 16};

下划线表示第一次折半判断位置，黄色标志位表示插入位置。

C++代码实现：

//折半插入排序
void BInsertSort(int l[], int n){
    for(int i=1; i<n; i++){
        int x = l[i];
        int low = 0;
        int high = i-1;
        while(low <= high){
            int m = (low + high) / 2;
            if(l[m] > x)    high = m-1;
            else low = m+1;
        }
        for(int j=i-1; j>=high+1;j--)
            l[j+1] = l[j];
        l[high+1] = x;
    }
    for(int i=0; i<n; i++){
        cout << l[i] <<" ";
    }
}
int main(){
    int p[] = {51, 22, 56, 81, 17, 22, 90, 16};
    //InsertSort(p, 8);
    BInsertSort(p, 8);
    return 0;
}

 

算法特点：（1）稳定排序；

　　　　　（2）只适用于顺序结构，不适用与链式结构；

　　　　　（3）适合初始记录无序，N 较大时情况。

---

希尔排序

 

希尔排序又称为缩小增量排序。

希尔排序实质上是采用分组排序的方法。先将待排序记录分割成几组，对每组都进行直接插入排序。然后增加每组的数据量，继续进行插入排序，最后当经过几次分组排序后，整个序列处于”基本有序“状态，在对所有记录进行一次直接插入排序。

希尔排序的基础是根据每次相隔 d（增量）的记录分为一组进行直接插入排序，d（增量）< N 且逐次减少。

 

演示：无序数组 p[] = {51, 22, 56, 81, 17, 23, 90, 16, 55, 99};

增量数组 d[] = {5, 3, 1};

第一步：

根据增量 d[0] = 5进行组合 ：{51, 23}， {22, 90}，{56, 16}，{81, 55}，{17, 99}

对每组都进行直接插入排序 ：{23, 51}， {22, 90}，{16, 56}，{55, 81}，{17, 99}

此时的无序数组进行了第一次组合排序后变化：

{ 23,  22,  16 ,  55,  17,  51 , 90, 56 , 81,  99 }

 

第二步：

根据增量d[1] = 3进行组合 ：{23,55,90,99}，{22,17,56}，{16,51,81}

对每组都进行直接插入排序 ：{23,55,90,99}，{17,22,56}，{16,51,81}

此时的无序数组进行了第二次组合排序后变化：

{ 23,  17,  16 ,  55,  22,  51 , 90, 56 , 81,  99 }

 

第三步：

根据增量 d[2] = 1进行组合：{ 23,  17,  16 ,  55,  22,  51 , 90, 56 , 81,  99 }

对该组合进行直接插入排序，最终得到有序序列：{16 17 22 23 51 55 56 81 90 99}

 

C++ 代码实现：

 

#include <iostream>
using namespace std;
void ShellInsert(int *p, int d, int plen){
    for(int i=d; i<plen;i++){
        if(p[i] < p[i-d]){
            int k, x = p[i]; //x 为临时变量
            for(k=i-d; k>=0&&x<p[k]; k-=d){
                p[k+d] = p[k]; //记录后移
            }
            p[k+d] = x;
        }
    }
}
//按照增量序列 d[n],对 p 进行希尔排序
void InsertSort(int *p, int d[], int dlen, int plen){
    for(int i=0;i<dlen;i++){
        ShellInsert(p, d[i], plen);
    }
}
int main()
{
    //待排序记录
    int p[] = {51, 22, 56, 81, 17, 23, 90, 16, 55, 99};
    int d[] = {5, 3, 1}; //增量数组
    InsertSort(p, d, sizeof(d)/sizeof(d[0]), sizeof(p)/sizeof(p[0]));
    for(int i=0; i<sizeof(p)/sizeof(p[0]);i++)
        cout << p[i] << " ";
    return 0;
}

 

算法特点：（1）记录跳跃式的移动导致算法是不稳定的；

　　　　　（2）只能用于顺序结构，不能用于链式表；

　　　　　（3）增量序列可以有各种取法，但应该使增量序列中的值除了1之外没有其他公子，并且最后一个增量必须为1；

　　　　　（4）记录总的比较次数和移动次数比直接插入排序少，N 越大时，效果越明显。适用于初始记录无序，N 很大时的情况。

---

 

冒泡排序

 

冒泡排序是最简单的一种交换排序。

它通过比较相邻的交换记录，如果发现逆序，则进行交换，从而使得较小的记录不断往前“浮动”（左移），或者是较大的记录向下“坠落”（右移），从而达到排序的结果。

 

演示： p[] = {51, 22, 56, 81, 17, 23, 90, 16};

 

第一次排序：

经过第一次冒泡排序后最大值90已经到了最右侧，此时的序列为 {22 51 56 17 23 81 16 90}

所以第二次排序结果为 ：{22 51 56 17 23 16 81 90}

第三次 ：                       {22 51 17 23 16 56 81 90}

第四次：                        {22 17 23 16 51 56 81 90}

第五次：                        {22 17 16 23 51 56 81 90}

…

第七次：                        {16 17 22 23 51 56 81 90}

 

C++代码实现：

#include <iostream>
using namespace std;
void BubbleSort(int *p, int len){
    int m = len;
    int flag = 1;
    while(m>0 && flag == 1){
        flag = 0;
        for(int i=0;i<m-1;i++){
            if(p[i] > p[i+1]){
                int x = p[i];p[i] = p[i+1]; p[i+1] = x;
                flag = 1;
            }
        }
        m--;
    }
}
int main()
{
    int p[] = {51, 22, 56, 81, 17, 23, 90, 16};
    BubbleSort(p, sizeof(p)/sizeof(p[0]));
    for(int i=0;i<sizeof(p)/sizeof(p[0]);i++)
        cout << p[i] << " ";
    return 0;
}

时间复杂度 O(N^2)，空间复杂度 O(1)

算法特点：（1）稳定排序；

　　　　　（2）可用于链式存储结构；

　　　　　（3）移动次数较多，算法平均时间性能比直接插入排序差。不适合初始记录无序，N 较大的情况。

---

快速排序

在待排序的记录 p[n] 中任取一个作为支点 pri，将记录表中小于pri的记录放在 pri 的左边，大于pri 的记录放在pri的右边，将记录表 p[n] 分为两个子表，然后对两个子表继续进行分表，将两个子表分为4个子表…..一直到记录表 p[n] 中的记录有序。

实例：int p[] = {51, 22, 56, 81, 17, 23, 90, 16};

 

初始 ：51, 22, 56, 81, 17, 23, 90, 16

第一次排序：{22 17 23 16} 51 {56 81 90}

第二次排序：{17 16} 22 {23} 51 56 81 90

第三次排序：16 17 22 23 51 56 81 90

#include <iostream>
using namespace std;
int Sort(int *p, int low, int high){
    int x = p[low];
    int pri = p[low];
    while(low<high){
        while(low<high && pri<=p[high]) --high;
        p[low] = p[high];
        while(low<high && pri>=p[low])  ++low;
        p[high] = p[low];
    }
    p[low] = x;
    return low;
}
void SQ(int *p, int low, int high){
    if(low<high){
        int pio = Sort(p, low, high);
        SQ(p, low, pio-1);
        SQ(p, pio+1, high);
    }
}
void QuitSort(int *p, int len){
    SQ(p,0,len);
}
int main()
{
    int p[] = {51, 22, 56, 81, 17, 23, 90, 16};
    QuitSort(p, sizeof(p)/sizeof(p[0]));
    for(int i=0;i<sizeof(p)/sizeof(p[0]);i++)   cout<< (p[i]) << " ";
    return 0;
}

时间复杂度：O(nlog2n)

空间复杂度：O(n)

算法特点：（1）记录非顺序的移动导致排序算法是不稳定的

　　　　　（2）适用于顺序结构，不适用于链式结构

 

---

等风来，不如追风去。