Python实现神经网络算法识别手写数字集
最近忙里偷闲学习了一点机器学习的知识,看到神经网络算法时我和阿Kun便想到要将它用Python代码实现。我们用了两种不同的方法来编写它。这里只放出我的代码。
MNIST数据集基于美国国家标准与技术研究院的两个数据集构建而成。
训练集中包含250个人的手写数字,其中50%是高中生,50%来自人口调查局。
每个训练集的数字图片像素为28x28。
MNIST数据集可通过 下载链接 下载,它包含以下内容:
- 训练集图像:train-images-idx3-ubyte.gz,包含60000个样本
- 训练集类标:train-labels-idx1-ubyte.gz,包含60000个类标
- 测试集图像:t10k-images-idx3-ubyte.gz,包含10000个样本
- 测试集类标:t10k-labels-idx1-ubyte.gz,包含10000个类标
关于神经网络算法的详解太过复杂,本人水平有限便不再描述,我这里只给出我们两人的代码。若想了解详情请移步谷歌或者百度。
StarMan
github项目地址:https://github.com/MyBules/Neural-Network

import os import numpy as np import struct import matplotlib.pyplot as plt import sys from scipy.special import expit def load_mnist(path, kind = 'train'): ''' 读取数据 :param path: 路径 :param kind: 文件类型 :return: images: 60000*784 labels:手写数字对应的类标(整数0~9) ''' labels_path = os.path.join(path, '%s-labels-idx1-ubyte' % kind) images_path = os.path.join(path, '%s-images-idx3-ubyte' % kind) with open(labels_path, 'rb') as lbpath: magic, n = struct.unpack('>II', lbpath.read(8)) labels = np.fromfile(lbpath, dtype=np.uint8) with open(images_path, 'rb') as imgpath: magic, num, rows, cols = struct.unpack(">IIII", imgpath.read(16)) images = np.fromfile(imgpath, dtype= np.uint8).reshape(len(labels), 784) # 28*28=784 return images, labels class NeuralNetMLP(object): def __init__(self, n_output, n_features, n_hidden=30, l1=0.0, l2=0.0, epochs=500, eta=0.001, alpha=0.0, decrease_const=0.0, shuffle=True, minibatches=1, random_state=None): ''' :param n_output: 输出单元 :param n_features: 输入单元 :param n_hidden: 隐层单元 :param l1: L1正则化系数 lamda :param l2: L2正则化系数 lamda :param epochs: 遍历训练集的次数(迭代次数) :param eta: 学习速率 :param alpha: 动量学习进度的参数,它在上一轮的基础上增加一个因子,用于加快权重更新的学习 :param decrease_const: 用于降低自适应学习速率 n 的常数 d ,随着迭代次数的增加而随之递减以更好地确保收敛 :param shuffle: 在每次迭代前打乱训练集的顺序,以防止算法陷入死循环 :param minibatches: 在每次迭代中,将训练数据划分为 k 个小的批次,为加速学习的过程,梯度由每个批次分别计算,而不是在整个训练集数据上进行计算。 :param random_state: ''' np.random.seed(random_state) self.n_output = n_output self.n_features = n_features self.n_hidden = n_hidden self.w1, self.w2 = self._initialize_weights() self.l1 = l1 self.l2 = l2 self.epochs = epochs self.eta = eta self.alpha = alpha self.decrease_const = decrease_const self.shuffle = shuffle self.minibatches = minibatches def _encode_labels(self, y, k): ''' :param y: :param k: :return: ''' onehot = np.zeros((k, y.shape[0])) for idx, val, in enumerate(y): onehot[val, idx] = 1.0 return onehot def _initialize_weights(self): ''' # 计算权重 :return: w1, w2 ''' w1 = np.random.uniform(-1.0, 1.0, size=self.n_hidden*(self.n_features + 1)) w1 = w1.reshape(self.n_hidden, self.n_features + 1) w2 = np.random.uniform(-1.0, 1.0, size=self.n_output*(self.n_hidden + 1)) w2 = w2.reshape(self.n_output, self.n_hidden + 1) return w1, w2 def _sigmoid(self, z): ''' expit 等价于 1.0/(1.0 + np.exp(-z)) :param z: :return: 1.0/(1.0 + np.exp(-z)) ''' return expit(z) def _sigmoid_gradient(self, z): sg = self._sigmoid(z) return sg * (1 - sg) def _add_bias_unit(self, X, how='column'): if how == 'column': X_new = np.ones((X.shape[0], X.shape[1] + 1)) X_new[:, 1:] = X elif how =='row': X_new = np.ones((X.shape[0]+1, X.shape[1])) X_new[1:,:] = X else: raise AttributeError("'how' must be 'column' or 'row'") return X_new def _feedforward(self, X, w1, w2): a1 = self._add_bias_unit(X, how='column') z2 = w1.dot(a1.T) a2 = self._sigmoid(z2) a2 = self._add_bias_unit(a2, how='row') z3 = w2.dot(a2) a3 = self._sigmoid(z3) return a1, z2, a2, z3, a3 def _L2_reg(self, lambda_, w1, w2): return (lambda_/2.0) * (np.sum(w1[:, 1:] ** 2) + np.sum(w2[:, 1:] ** 2)) def _L1_reg(self, lambda_, w1, w2): return (lambda_/2.0) * (np.abs(w1[:,1:]).sum() + np.abs(w2[:, 1:]).sum()) def _get_cost(self, y_enc, output, w1, w2): term1 = -y_enc * (np.log(output)) term2 = (1 - y_enc) * np.log(1 - output) cost = np.sum(term1 - term2) L1_term = self._L1_reg(self.l1, w1, w2) L2_term = self._L2_reg(self.l2, w1, w2) cost = cost + L1_term + L2_term return cost def _get_gradient(self, a1, a2, a3, z2, y_enc, w2, w1): # 反向传播 sigma3 = a3 - y_enc z2 = self._add_bias_unit(z2, how='row') sigma2 = w2.T.dot(sigma3) * self._sigmoid_gradient(z2) sigma2 = sigma2[1:, :] grad1 = sigma2.dot(a1) grad2 = sigma3.dot(a2.T) # 调整 grad1[:, 1:] += (w1[:, 1:] * (self.l1 + self.l2)) grad2[:, 1:] += (w2[:, 1:] * (self.l1 + self.l2)) return grad1, grad2 def predict(self, X): a1, z2, a2, z3, a3 = self._feedforward(X, self.w1, self.w2) y_pred = np.argmax(z3, axis=0) return y_pred def fit(self, X, y, print_progress=False): self.cost_ = [] X_data, y_data = X.copy(), y.copy() y_enc = self._encode_labels(y, self.n_output) delta_w1_prev = np.zeros(self.w1.shape) delta_w2_prev = np.zeros(self.w2.shape) for i in range(self.epochs): # 自适应学习率 self.eta /= (1 + self.decrease_const*i) if print_progress: sys.stderr.write('\rEpoch: %d/%d' % (i+1, self.epochs)) sys.stderr.flush() if self.shuffle: idx = np.random.permutation(y_data.shape[0]) X_data, y_data = X_data[idx], y_data[idx] mini = np.array_split(range(y_data.shape[0]), self.minibatches) for idx in mini: # 前馈 a1, z2, a2, z3, a3 = self._feedforward(X[idx], self.w1, self.w2) cost = self._get_cost(y_enc=y_enc[:, idx], output=a3, w1=self.w1, w2=self.w2) self.cost_.append(cost) # 通过反向传播计算梯度 grad1, grad2 = self._get_gradient(a1=a1, a2=a2, a3=a3, z2=z2, y_enc=y_enc[:, idx], w1=self.w1, w2=self.w2) # 更新权重 delta_w1, delta_w2 = self.eta * grad1, self.eta * grad2 self.w1 -= (delta_w1 + (self.alpha * delta_w1_prev)) self.w2 -= (delta_w2 + (self.alpha * delta_w2_prev)) delta_w1_prev, delta_w2_prev = delta_w1, delta_w2 return self def costplt1(nn): '''代价函数图象''' plt.plot(range(len(nn.cost_)), nn.cost_) plt.ylim([0, 2000]) plt.ylabel('Cost') plt.xlabel('Epochs * 50') plt.tight_layout() plt.show() def costplt2(nn): '''代价函数图象''' batches = np.array_split(range(len(nn.cost_)), 1000) cost_ary = np.array(nn.cost_) cost_avgs = [np.mean(cost_ary[i]) for i in batches] plt.plot(range(len(cost_avgs)), cost_avgs, color='red') plt.ylim([0, 10000]) plt.ylabel('Cost') plt.xlabel('Epochs') plt.tight_layout() plt.show() if __name__ == '__main__': path = 'mnist' # 路径 # images, labels = load_mnist(path) # print(np.shape(images), labels) # 训练样本和测试样本 X_train, y_train = load_mnist(path, kind='train') # X_train : 60000*784 # print(np.shape(X_train),y_train) X_test, y_test = load_mnist(path, kind='t10k') # X_test : 10000*784 # print(np.shape(X_test), y_test) nn = NeuralNetMLP(n_output=10, n_features=X_train.shape[1], n_hidden=50, l2=0.1, l1=0.0, epochs=1000, eta=0.001, alpha=0.001, decrease_const=0.00001, shuffle=True, minibatches=50, random_state=1) nn.fit(X_train, y_train, print_progress=True) costplt1(nn) costplt2(nn) y_train_pred = nn.predict(X_train) acc = np.sum(y_train == y_train_pred, axis=0) / X_train.shape[0] print('训练准确率: %.2f%%' % (acc * 100)) y_test_pred = nn.predict(X_test) acc = np.sum(y_test == y_test_pred, axis=0) / X_test.shape[0] print('测试准确率: %.2f%%' % (acc * 100)) # 错误样本 miscl_img = X_test[y_test != y_test_pred][:25] correct_lab = y_test[y_test != y_test_pred][:25] miscl_lab = y_test_pred[y_test != y_test_pred][:25] fig, ax = plt.subplots(nrows=5, ncols=5, sharex=True, sharey=True,) ax = ax.flatten() for i in range(25): img = miscl_img[i].reshape(28, 28) ax[i].imshow(img, cmap='Greys', interpolation='nearest') ax[i].set_title('%d) t: %d p: %d' % (i+1, correct_lab[i], miscl_lab[i])) ax[0].set_xticks([]) ax[0].set_yticks([]) plt.tight_layout() plt.show() # 正确样本 unmiscl_img = X_test[y_test == y_test_pred][:25] uncorrect_lab = y_test[y_test == y_test_pred][:25] unmiscl_lab = y_test_pred[y_test == y_test_pred][:25] fig, ax = plt.subplots(nrows=5, ncols=5, sharex=True, sharey=True, ) ax = ax.flatten() for i in range(25): img = unmiscl_img[i].reshape(28, 28) ax[i].imshow(img, cmap='Greys', interpolation='nearest') ax[i].set_title('%d) t: %d p: %d' % (i + 1, uncorrect_lab[i], unmiscl_lab[i])) ax[0].set_xticks([]) ax[0].set_yticks([]) plt.tight_layout() plt.show()
测试结果:

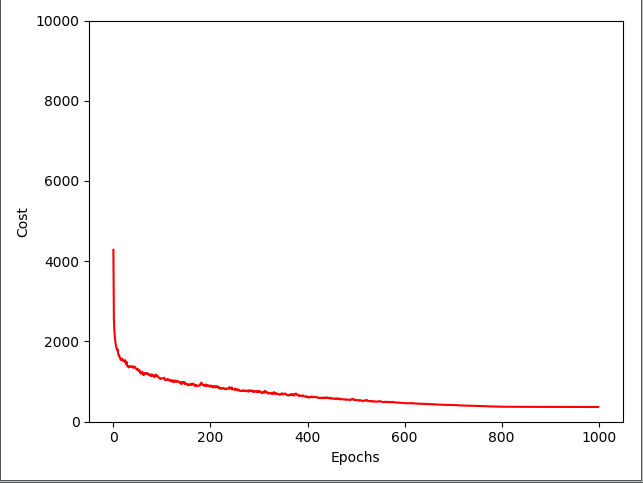
代价函数图像:
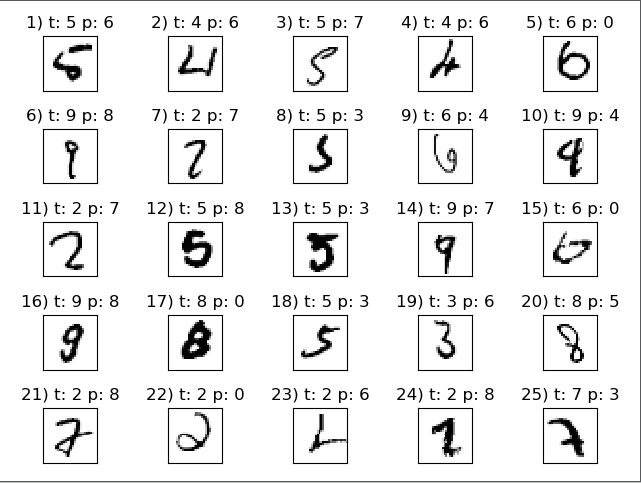
测试错误样本:
测试正确样本:




