Java中的队列

关于队列

队列（Queue）是一个基于链接节点的无界线程安全队列，它采用先进先出的规则对节点进行排序，当我们添加一个元素的时候，它会添加到队列的尾部，当我们获取一个元素时，它会返回队列头部的元素。

如下图，可以把队列比作成排队领票的一队人，先到的人先领票，后到的人后拿票。

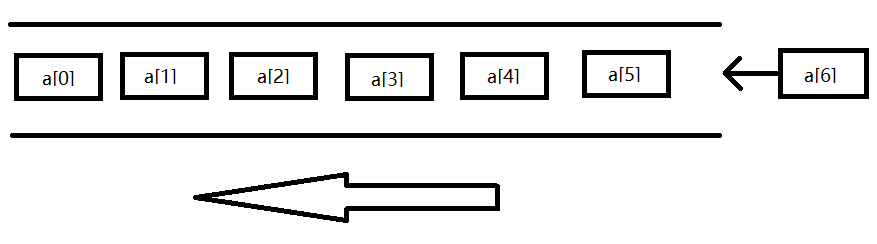
队列可以同时对头和尾进行操作，如果我定义一个数组，我可以取出头a[o]，也可以在a[5]后面添加新的元素a[6]。

 

关于 Queue 接口

队列的方法摘要

修饰语和类型	方法和说明
boolean	add(E e)           将指定的元素插入此队列（如果立即可行且不会违反容量限制），在成功时返回 true，如果当前没有可用的空间，则抛出 IllegalStateException。
E	element()           获取，但是不移除此队列的头。
boolean	offer(E e)           将指定的元素插入此队列（如果立即可行且不会违反容量限制），当使用有容量限制的队列时，此方法通常要优于 add(E)，后者可能无法插入元素，而只是抛出一个异常。
E	peek()           获取但不移除此队列的头；如果此队列为空，则返回 null。
E	poll()           获取并移除此队列的头，如果此队列为空，则返回 null。
E	remove()           获取并移除此队列的头。

 

 

 

 

 

 

 

 

 

 

 

实例

这里我暂且用数组来实现栈

ps:我这里用了java的泛型，关于java的泛型在前面的随笔里我有介绍。

 

import java.util.Arrays;

public class Queue<E> {

    // 新建一个长度为0的数组
    private Object[] src = new Object[0];

    // 将数据加入队列
    public void add(E s) {
        // 复制src数组，长度为原数组的长度+1
        E[] e = (E[]) Arrays.copyOf(src, src.length + 1);
        // 将传入的数据给新数组的最后一个元素
        e[e.length - 1] = (E) s;
        src = e;
    }

    // 查看队列头的数据
    public E peek() {
        //判断队列是否为空
        if(src.length==0) {
            return null;
        }
        // 返回src数组的第一个元素
        return (E) src[0];
    }

    // 弹出队列头的数据[移除]
    public E poll() {
        if (src.length == 0) {
            return null;
        }
        //将src数组复制给新数组，方便弹出队列头的数据
        E[] s = (E[]) Arrays.copyOf(src, src.length);
        //新建一个长度为原数组长度-1的数组，将原数组去掉第一个元素后复制给新数组
        Object[] st =new Object[src.length - 1];
        for (int i = 0; i < st.length; i++) {
            st[i] = (E) src[i + 1];
        }
        src = st;
        return s[0];
    }

    // 获得队列的长度
    public int size() {
        return src.length;
    }

    // 判断队列是否为空
    public boolean empty() {
        return src.length == 0;
    }
    
    public static void main(String[] args) {
        Queue<String> q=new Queue<String>();
        
        //将数据加入队列
        q.add("AA");
        q.add("BB");
        q.add("CC");
        q.add("DD");
        
        System.out.println("队列头的数据为："+q.peek());
        
        System.out.println("队列的长度为："+q.size());
        
        while(!q.empty()) {
            System.out.println("弹出数据："+q.poll());
        }
    }
}

运行结果：

队列头的数据为：AA
队列的长度为：4
弹出数据：AA
弹出数据：BB
弹出数据：CC
弹出数据：DD

 

结果分析

遵循了队列 ‘ 先进先出 ’ 的特性，输入 AA、BB、CC、DD，弹出 AA、BB、CC、DD。

根据这个特性，队列在某些时候是必不可少的。