|
(六)非线性分位数回归
这里的非线性函数为Frank copula函数。
|
## Demo of nonlinear quantile regression model based on Frank copula
vFrank <- function(x, df, delta, u) # 某个非线性过程,得到的是[0,1]的值
-log(1-(1-exp(-delta))/(1+exp(-delta*pt(x,df))*((1/u)-1)))/delta
# 非线性模型
FrankModel <- function(x, delta, mu,sigma, df, tau) {
z <- qt(vFrank(x, df, delta, u = tau), df)
mu + sigma*z
}
n <- 200 # 样本量
df <- 8 # 自由度
delta <- 8 # 初始参数
set.seed(1989)
x <- sort(rt(n,df)) # 生成基于T分布的随机数
v <- vFrank(x, df, delta, u = runif(n)) # 基于x生成理论上的非参数对应值
y <- qt(v, df) # v 对应的T分布统计量
windows(5,5)
plot(x, y, pch="o", col="blue", cex = .25) # 散点图
Dat <- data.frame(x = x, y = y) # 基本数据集
us <- c(.25,.5,.75)
for(i in 1:length(us)){
v <- vFrank(x, df, delta, u = us[i])
lines(x, qt(v,df)) # v为概率,计算每个概率对应的T分布统计量
}
cfMat <- matrix(0, 3, length(us)+1) # 初始矩阵,用于保存结果的系数
for(i in 1:length(us)) {
tau <- us[i]
cat("tau = ", format(tau), ".. ")
fit <- nlrq(y ~ FrankModel(x, delta,mu,sigma, df = 8, tau = tau), # 非参数模型
data = Dat, tau = tau, # data表明数据集,tau分位数回归的分位点
start= list(delta=5, mu = 0, sigma = 1), # 初始值
trace = T) # 每次运行后是否把结果显示出来
lines(x, predict(fit, newdata=x), lty=2, col="red") # 绘制预测曲线
cfMat[i,1] <- tau # 保存分位点的值
cfMat[i,2:4] <- coef(fit) # 保存系数到cfMat矩阵的第i行
cat("\n") # 如果前面把每步的结果显示出来,则每次的结果之间添加换行符
}
colnames(cfMat) <- c("分位点",names(coef(fit))) # 给保存系数的矩阵添加列名
cfMat
|
结果:
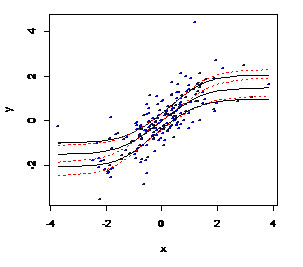
图2.5 非参数散点图、真实T分布和拟合结果的比较
拟合结果:(过程略)
> cfMat
分位点 delta mu sigma
[1,] 0.25 14.87165 -0.20530041 0.9134657
[2,] 0.50 16.25362 0.03232525 0.9638209
[3,] 0.75 12.09836 0.11998614 0.9423476
(七)半参数和非参数分位数回归
非参数分位数回归在局部多项式的框架下操作起来更加方便。可以基于以下函数。
|
# 2-7-1 半参数模型----
fit<-rq(y~bs(x,df=5)+z,tau=.33)
# 其中bs()表示按b-spline的非参数拟合
# 2-7-2 非参数方法
lprq <-function(x,y,h,m=50,tau=0.5){
# 这是自定义的一个非参数计算函数,在其他数据下同样可以使用
xx<-seq(min(x),max(x),length=m) # m个监测点
fv<-xx
dv<-xx
for(i in 1:length(xx)){
z<-x-xx[i]
wx<-dnorm(z/h) # 核函数为正态分布,dnorm计算标准正态分布的密度值
r<-rq(y~z,weights=wx,tau=tau, # 上面计算得到的密度值为权重
ci=FALSE)
fv[i]<-r$coef[1]
dv[i]<-r$coef[2]
}
list(xx=xx,fv=fv,dv=dv) # 输出结果
}
library(MASS)
data(mcycle)
attach(mcycle)
windows(5,5) # 非参数的结果一般是通过画图查看的
plot(times,accel,xlab="milliseconds",ylab="acceleration")
hs<-c(1,2,3,4) # 选择不同窗宽进行估计
for(i in hs){
h=hs[i]
fit<-lprq(times,accel,h=h,tau=0.5) # 关键拟合函数
lines(fit$xx,fit$fv,lty=i)
}
legend(45,-70,c("h=1","h=2","h=3","h=4"),
lty=1:length(hs))
|
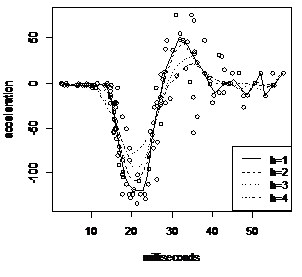
结果:
图2.6 基于正态分布为核函数的非参数拟合结果
|
# 2-7-3 非参数回归的另一个方法----
# 考察较大的跑步速度与体重的关系
data(Mammals)
attach(Mammals)
x<-log(weight) # 取得自变量的值
y<-log(speed) # 取得因变量的值
plot(x,y,xlab="Weightinlog(Kg)",ylab="Speedinlog(Km/hour)",
type="n")
points(x[hoppers],y[hoppers],pch="h",col="red")
points(x[specials],y[specials],pch="s",col="blue")
others<-(!hoppers&!specials)
points(x[others],y[others],col="black",cex=0.75)
fit<-rqss(y~qss(x,lambda=1),tau=0.9) # 关键的拟合步骤
plot(fit,add=T) # add=T表示在上图中添加这里的曲线
|
结果:
图2.7 90%分位点下的附加分位数回归拟合结果
(八)分位数回归的分解
|
# MM2005分位数分解的函数,改变参数可直接使用
MM2005 = function(formu,taus, data, group, pic=F){
# furmu 为方程,如foodexp~income
# taus 为不同的分位数
# data 总的数据集
# group 分组指标,是一个向量,用于按行区分data
# pic 是否画图,如果分位数比较多,建议不画图
engel1 = data[group==1,]
engel2 = data[group==2,]
# 开始进行分解
fita = summary( rq(formu, tau = taus, data = engel1 ) )
fitb = summary( rq(formu, tau = taus, data = engel2 ) )
tab = matrix(0,length(taus),4)
colnames(tab) = c("分位数","总差异","回报影响","变量影响")
rownames(tab) = rep("",dim(tab)[1])
for( i in 1:length(taus) ){
ya = cbind(1,engel1[,names(engel1)!=formu[[2]]] ) %*% fita[[i]]$coef[,1]
yb = cbind(1,engel2[,names(engel2)!=formu[[2]]] ) %*% fitb[[i]]$coef[,1]
# 这里以group==1为基准模型,用group==2的数据计算反常规模型拟合值
ystar = cbind(1,engel2[,names(engel2)!=formu[[2]]] ) %*% fita[[i]]$coef[,1]
ya = mean(ya)
yb = mean(yb)
ystar = mean(ystar)
tab[i,1] = fita[[i]]$tau
tab[i,2] = yb - ya
tab[i,3] = yb - ystar # 回报影响,数据相同,模型不同:模型机制的不同所产生的差异
tab[i,4] = ystar - ya # 变量影响,数据不同,模型相同:样本点不同产生的差异
}
# 画图
if( pic ){
attach(engel)
windows(5,5)
plot(income, foodexp, cex=0.5, type="n",main="两组分位数回归结果比较")
points(engel1, cex=0.5, col=2)
points(engel2, cex=0.5, col=3)
for( i in 1:length(taus) ){
abline( fita[[i]], col=2 )
abline( fitb[[i]], col=3 )
}
detach(engel)
}
# 输出结果
tab
}
# 下面是用一个样本数据做的测试
data(engel)
group = c(rep(1,100),rep(2,135)) # 取前100个为第一组,后135个第二组
taus = c(0.05,0.25,0.5,0.75,0.95) # 需要考察的不同分位点
MM2005(foodexp~income, taus, data = engel, group=group, pic=F) # 参数说明,见①
|
说明:① 自编函数MM2005的参数说明:
函数调用形式MM2005 (formu, taus, data, group, pic=F),其中
# furmu 为回归方程,如foodexp~income;
# taus 为不同的分位数,如taus=c(0.05,0.5,0.95);
# data 总的数据集,如上例中的engel数据集;
# group 分组指标,是一个向量,用于按行区分data,第一组为1,第二组为2;目前仅能分两组;
# pic 逻辑参数:是否画图。如果分位数比较多,建议不画图;默认不画图,pic=F;如果想画图,则添加参数pic=T。
② 最终结果:
> MM2005(foodexp~income, taus, data = engel, group=group, pic=F)
分位数 总差异 回报影响 变量影响
0.05 -30.452061 -72.35939 41.90733
0.25 -2.017317 -46.20125 44.18394
0.50 30.941212 -23.24042 54.18163
0.75 43.729025 -15.76283 59.49185
0.95 52.778985 -11.29932 64.07830
|




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步