栈、队列、链表
2.1 汉诺塔游戏——栈
应该有一部分人在小时候听说过汉诺塔这个游戏。我记得在小时候曾非常流行买电子词典来学习英语,基本上每个人都有一本电子词典。在电子词典中也预设了几个益智的小游戏,其中一个就是汉诺塔。
2.1.1 什么是汉诺塔
汉诺塔是印度的一个古老的益智玩具,其基本设置如图2-1所示。
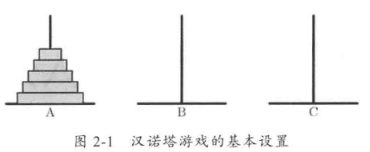
这个游戏的目标是,把A上的所有圆盘重新按顺序堆到C上,但是有两个规则,一是小圆盘不能放置在大圆盘下面,二是每次只能移动一个圆盘。
怎么才能完成这个游戏?大家可以先思考一下。
我们先来举个简单的例子:假如只有三个圆盘,那么怎么玩呢?为了描述方便,我们按照从小到大的顺序将圆盘分别编号为1、2、3号。
最初,三个圆盘都在A柱子上,开始后每次只能移动一个圆盘,那么将1号圆盘放到B上,还是C上?如果将1号圆盘放到B上,那么根据小圆盘不能处于大圆盘之下的规则,2号圆盘只能放到C上:当把1号圆盘放回到2号圆盘上时,1、2号圆盘都在C上,之后再要移动的3号圆盘只能放到B上了。这时你可能会想:如果游戏的目标是把圆盘移动到B上该多好啊,那么此刻就快完成了。但游戏的目标是将所有圆盘按顺序移动到C上。当然,现在圆盘比较少,肯定能完成目标,只是移动的次数有些多。我们反过来思考一下,一开始把1号圆盘移动到C上,这样移动的步数是最少的。
通过这个动手操作的过程,我们反过来思考一下,怎么移动才能让最大的圆盘到最后刚好放到C上?
假设圆盘总数为N,那么我们需要先把上面N-1个圆盘从A移动到B上,然后第N个圆盘才能移动到C上,之后再把B上N-1个圆盘移动到C上,又该怎么移动?此时必须先把最小的N-2个圆盘从B上全部移动到A上,第N-1个圆盘才能移动到C上,同理可依次完成剩下圆盘的移动,直至最终完成游戏。
2.1.2 什么是栈
栈是一个有着特殊规则的数据结构。我们在前面了解了汉诺塔游戏,这里有一个明确的规则,即每次只能移动顶端的一个圆盘。
栈也有这个特点。我们可以将栈视为汉诺塔中的一个柱子,我们往这个柱子上放置圆盘,先放下去的一定是最后才能拿出来的,而最后放下去的一定是最先拿出来的。这也是栈的最重要一个特点——后进先出(LIFO,Last In First Out),也可以说是先进后出(FILO,First In Last Out),我们无论如何只能从一端去操作元素。
栈又叫作堆栈(Stack),这里说明一下不要将它和堆混淆。实际上堆和栈是两个不同的概念,栈是一种只能在一端进行插入和删除的线性数据结构。
一般来说,栈主要有两个操作:一个是进栈(PUSH),又叫作入栈、压栈;另一个是出栈(POP),或者叫作退栈。
其实栈是一种比较简单的数据结构,但是由于其特性,又衍生了不少的相关算法。
2.1.3 栈的存储结构
栈一般使用一段连续的空间进行存储,通常预先分配一个长度,可以简单地使用数组去实现,具体的存储结构如图2-2所示。
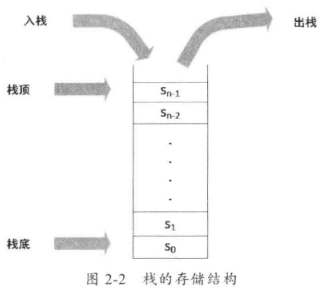
通过图2-2可以清晰地看到,只有一个方向可以对栈内的元素进行操作,而栈中最下面的一个元素成为栈底,一般是数组的第0个元素,而栈顶是栈内最后放入的元素。
一般而言,定义一个栈需要有一个初始的大小,这就是栈的初始容量。当需要放入的元素大于这个容量时,就需要进行扩容。栈扩容的实现类似于在第1章中介绍的集合。
栈出入元素的操作如下。例如我们初始化一个长度为10的数组,并向其中放入元素,根据栈的定义,只能从数组的一端放入元素,我们设定这一端为数组中较大下标的方向。我们放入第1个元素,由于栈内没有元素,于是第1个元素就落到了数组的第0个下标的位置上;接着放入第2个元素,第2个元素该放入下标为1的位置上:以此类推,当放入了5个元素时,第5个入栈的元素应该在数组的第4个下标的位置上。现在我们要进行出栈操作,出栈只能从一端操作,我们之前设定只能从数组下标较大的方向操作,因此需要确定数组中下标最大的一个方向中存在栈元素的位置下标是多少。我们一般会在栈中做个计数器来记录这个值。现在栈中有5个元素,所以将数组中的第5个位置也就是下标为4的元素出栈。此时数组中只剩下4个元素了。
下面是栈的实现代码,这里以整型元素为例,在Java类的高级语言中,数据类型可以换成对象。
public class Test2 { public static void main(String[] args) { MyStack stack = new MyStack(1);// 为了方便看出效果,设定初始数组长度为1 stack.push(1); stack.push(2); System.out.println(stack.size());// 栈内元素个数为2,当前数组长度也为2 stack.push(3); System.out.println(stack.size());// 栈内元素个数为3,当前数组长度为4 System.out.println(stack.peek());// 获取栈顶元素,为3,但是没有出栈 System.out.println(stack.size());// 由于上面一行没有出栈,所以元素个数还是为3 System.out.println(stack.pop());// 栈顶元素出栈,返回3 System.out.println(stack.pop());// 栈顶元素出栈,返回2 System.out.println(stack.size());// 出了两次栈,当前元素个数为1 } } class MyStack { private int size = 0; private int[] array; public MyStack() { array = new int[10]; } public MyStack(int init) { if (init <= 10) { init = 10; } array = new int[init]; } /** * 入栈 * * @param item */ public void push(int item) { if (size == array.length) { array = Arrays.copyOf(array, size * 2); } array[size++] = item; } /** * 获取栈顶元素,但是没有出栈 * * @return */ public int peek() { if (size == 0) { throw new IndexOutOfBoundsException("栈里已经空了"); } return array[size - 1]; } /** * 出栈,同时获取栈顶元素 * * @return */ public int pop() { int item = peek(); size--;// 直接使元素个数减1,不需要真的清除元素,下次入栈会覆盖旧元素的值 return item; } /** * 栈是否满了 * * @return */ public boolean isFull() { return size == array.length; } /** * 栈是否为空栈 * * @return */ public boolean isEmpity() { return size == 0; } public int size() { return size; } }
2.1.4 栈的特点
栈的特点是显而易见的,只能在一端进行操作,遵循先进后出或者后进先出的原则。
2.1.5 栈的适用场景
什么时候使用栈?根据栈先进先出且只能在一端操作的特点,一般有下面几个应用。
(1)逆序输出
由于栈具有先进后出的特点,所以逆序输出是其中一个非常简单的应用。首先把所有元素按顺序入栈,然后把所有元素出栈并输出,轻松实现逆序输出。
(2)语法检查,符号成对出现
在编程语言中.一般括号都是成对出现的,比如“[”和“]”“{”和“}”“(”和“)”“<”和“>”(这里的“<”和“>”排除了作为大于小于号的情况)。
凡是遇到括号的前半部分,即为入栈符号(PUSH);凡是遇到括号的后半部分,就比对是否与栈顶元素相匹配(PEEK),如果相匹配,则出栈(POP),否则就是匹配出错。
(3)数制转换(将十进制的数转换为2~9的任意进制的数)
另一个应用就是用于实现十进制与其他进制的转换规则。
通过求余法,可以将十进制数转换为其他进制,比如要转为八进制,则将原十进制数除以8,记录余数,然后继续将商除以8,一直到商等于0为止,最后将余数倒着写出来就行了。
依照这个原理,当我们要将100转为八进制数时,先将100除以8,商12余4,第1个余数4入栈:之后继续用12除以8,商1余4,第2个余数4入栈;接着用1除以8,商0余1,第3个余数1入栈。最后将三个余数全部出栈,就得到了100的八进制数144。
当然,栈的应用不仅有这些,其他应用还有很多。比如常听到的编程语言调用中的“函数栈”,就是我们在调用方法时计算机会执行PUSH方法,记录调用,在return也就是方法结束之后,执行POP方法,完成前后对应。
2.2 火爆的奶茶店——队列
台湾的奶茶店非常有名,有些店前经常大排长龙。如果想要购买一杯奶茶,则得到队伍末尾去排队,等待队伍前面的人逐个按顺序付款、取奶茶之后,才轮得到自己付钱、取奶茶,排在自己之后的人也是这样购买奶茶的。
当然,现在的一些奶茶店已经开始采取付款之后出排号小票的方式进行售卖了,这样就为制作奶茶提供了一个缓冲时间,相当于将一个队伍分成了两个队伍,付款队伍排完了就会进入取奶茶队伍,提高了奶茶店整体的操作速度。
2.2.1 什么是队列
什么是队列?队列就是一个队伍。队列和栈一样,由一段连续的存储空间组成,是一个具有自身特殊规则的数据结构。我们在2.1节说到栈是后进先出的规则,队列刚好与之相反,是一个先进先出(FIFO,First In First Out)或者说后进后出(LILO,Last In Last Out)的数据结构。想象一下,在排队时是不是先来的就会先从队伍中出去呢?
队列是一种受限的数据结构,插入操作只能从一端操作,这一端叫作队尾;而移除操作也只能从另一端操作,这一端叫作队头。针对上面购买奶茶队伍的例子,排在收银员一端的就是队头,而新来的人则要排到队尾。
我们将没有元素的队列称为空队,也就是在没人要购买奶茶时,就没人排队了。往队列中插入元素的操作叫作入队,相应地,从队列中移除元素的操作叫作出队。
一般而言,队列的实现有两种方式:数组和链表。这里又提到了链表,我们暂时先不做讲解。用数组实现队列有两种方式,一种是顺序队列,一种是循环队列。这两种队列的存储结构及特点在之后进行介绍。
用数组实现队列,若出现队列满了的情况,则这时就算有新的元素需要入队,也没有位置。此时一般的选择是要么去掉,要么等待,等待的时间一般会有程序控制。
2.2.2 队列的存储结构
顺序队列的存储结构如图2-3所示。

顺序队列会有两个标记,一个是队头位置(head),一个是下一个元素可以插入的队尾位置(tail)。一开始两个标记都指向数组下标为0的位置,如图2-4所示。
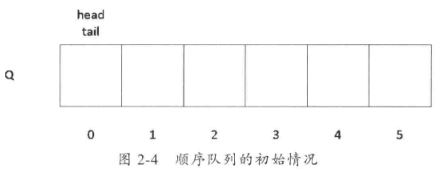
在插入元素之后,tail 标记就会加1,比如入队三个元素,分别为A、B、C,则当前标记及存储情况如图2-5所示。
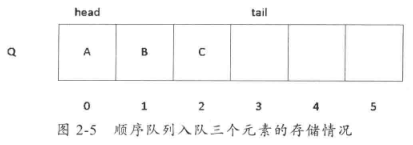
当前head为0时,tail为3。接下来进行出队操作,出队一个元素,head指向的位则加1,比如进行一次出队操作之后,顺序队列的存储情况如图2-6所示。

因此,在顺序队列中,队列中元素的个数我们可以用tail减去head计算。当head与tail相等时,队列为空队,当tail达到数组长度,也就是队列存储之外的位置时,说明这个队列已经无法再容纳其他元素入队了。空间是否都满了?并没有,由于两个标记都是只增不减,所以两个标记最终都会到数组的最后一个元素之外,这时虽然数组是空的,但也无法再往队列里加入元素了。
当队列中无法再加入元素时,我们称之为“上溢”;当顺序队列还有空间却无法入队时,我们称之为“假上溢”:如果空间真的满了,则我们称之为“真上溢”;如果队列是空的,则执行出队操作,这时队列里没有元素,不能出队,我们称之为“下溢”,就像奶茶店根本没人排队,收银员也就没法给别人开出消费单了。
怎么解决顺序队列的“假上溢”问题呢?这时就需要采用循环队列了。
当顺序队列出现假上溢时,其实数组前端还有空间,我们可以不用把标记指向数组外的地方,只需要把这个标记重新指向开始处就能解决。想象一下这个数组首尾相接,成为一个圈。存储结构还是之前提到的,在一个数组上。此时,如果当前队列中元素的情况如图2-7所示,那么在入队E、F元素时,存储结构会如图2-8所示。

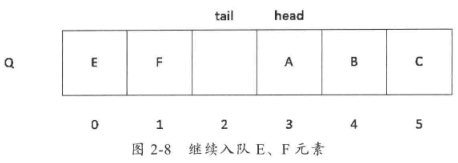
一般而言。我们在对head或者tail加1时,为了方便,可直接对结果取余数组长度,得到我们需要的数组长度。另外由于顺序队列存在“假上溢”的问题,所以在实际使用过程中都是使用循环队列来实现的。
但是循环队列中会出现这样一种情况:当队列没有元素时,head等于tail,而当队列满了时,head也等于tail。为了区分这两种状态,一般在循环队列中规定队列的长度只能为数组总长度减1,即有一个位置不放元素。因此,当head等于tail时,说明队列为空队,而当head等于 (tail+1)%length 时(length为数组长度),说明队满。
下面为顺序列队的代码实现。
package com.example.demo.base.queue; public class MyArrayQueue { private Object[] items; private int head; private int tail; /** * 初始化队列 * * @param capacity */ public MyArrayQueue(int capacity) { this.items = new Object[capacity]; } /** * 入队 * * @param item * @return */ public boolean put(Object item) { if (head == (tail + 1) % items.length) { //说明队满 return false; } items[tail] = item; tail = (tail + 1) % items.length;//tail标记向后移动一位 return true; } /** * 获取队列头元素,不出队 * * @return */ public Object peek() { if (head == tail) { //说明队列为空 return null; } return items[head]; } /** * 出队 * * @return */ public Object poll() { if (head == tail) { //说明队列为空 return null; } Object item = items[head]; items[head] = null;//把没用的元素赋空值,当然不设置也可以,反正标记移动了,之后会被覆盖 head = (head + 1) % items.length;//head标记向后移动一位 return item; } public boolean isFull() { return head == (tail + 1) % items.length; } public boolean isEmpty() { return head == tail; } public int size() { if (tail >= head) { return tail - head; } else { return tail + items.length - head; } } }
测试代码
public class TestMyArrayQueue { public static void main(String[] args) { MyArrayQueue queue = new MyArrayQueue(4); System.out.println(queue.put("A"));//true System.out.println(queue.put("B"));//true System.out.println(queue.put("C"));//true System.out.println(queue.put("D"));//false System.out.println(queue.isFull());//true,当队列已经满了,并且D元素没用入队成功 System.out.println(queue.size());//3,队列中有三个元素 System.out.println(queue.peek());//A,获取队头元素,不出队 System.out.println(queue.poll());//A System.out.println(queue.poll());//B System.out.println(queue.poll());//C System.out.println(queue.isEmpty());//true,当队列为空队 } }
在上面的代码中尽管声明的长度是4,但是只能放入3个元素,这里是通过在初始化数组时多设置一个位置来解决问题的:也可以通过增加一个变量来记录元素的个数去解决问题,不需要两个标记去确定是队空还是队满,元素也能放满而不用空出一位了。
2.2.3 队列的特点
队列的特点也是显而易见的,那就是先进先出。出队的一头是队头,入队的一头是队尾。当然,队列一般来说都会规定一个有限的长度,叫作队长。
2.2.4 队列的适用场景
队列在实际开发中是很常用的。在一般程序中会将队列作为缓冲器或者解耦使用。下面举几个例子具体说明队列的用途。
注:解耦,即当一个项目发展得比较大时,必不可少地要拆分各个模块。为了尽可能地让各个模块独立,则需要解耦,即我们常听说的高内聚.低耦合。如何对各模块进行解耦?其中一种方式就是通过消息队列。
1. 某品牌手机在线秒杀用到的队列
现在,某个品牌的手机推出新型号,想要购买就需要上网预约,到了开抢时间就得赶紧打开网页守着,疯狂地刷新页面,疯狂地点击抢购按钮。一般在每次秒杀中提供的手机只有几千部。假设有两百万人抢购,则从开抢的这一秒开始,两百万人都开始向服务器发送请求。如果服务器能直接处理请求,把抢购结果立刻告诉用户,同时为抢购成功的用户生成订单,让用户付款购买手机,则这对服务器的要求很高,很难实现。那么该怎么解决呢?解决方法是:在接收到每个请求之后,把这些请求按顺序放入队列的队尾中,然后提示用户“正在排队中”,接下来用户开始排队:而在这个队列的另一端,也就是队头,会有一些服务器在处理,根据先后顺序告知用户抢购结果。
这就出现了抢购手机时,抢购界面稍后才告诉我们抢购结果的情况。我有个朋友在抢购成功之后,抢购界面提示他稍后去订单中查看结果,当他查看订单却没有发现新订单,其实是因为他的请求已经进入了服务器处理的队列,服务器处理完之后才会为他生成订单。
注:这种方式也叫作异步处理。异步与同步是相对的,同步是在一个调用执行完成之后,等待调用结束返回;而异步不会立刻返回结果,返回结果的时间是不可预料的,在另一端的服务器处理完成之后才有结果,如何通知执行的结果又是另一回事。
2. 生产者和消费者模式
有个非常有名的设计模式,叫作生产者和消费者模式。这个设计模式就像有一个传送带,生产者在传送带这头将生产的货物放上去,消费者在另一头逐个地将货物从传送带上取下来。这个设计模式的实现原理也比较简单,即存在一个队列,若干个生产者同时向队列中添加元素,然后若干个消费者从队列中获取元素。
这时参考奶茶店的例子,每个购买奶茶的人就是一个生产者,依次进入第1个队列中,收银员就是一个消费者(假设这个收银员称为消费者A),负责“消费”队列中的购买者,让购买者逐个从队列中出来。通过提供给购买者带有编号的一张小票,让购买者进入了第2个队列。此时收很员在第2个队列中又作为生产者出现。
第2个队列的消费者是谁?是制作奶茶的店员,这里称之为消费者B。而一般规模较大的奶茶店,制作奶茶的店员会较多,假设有两人以上,即消费者B比消费者A多。此时第2个队列就起到了缓冲的作用,达到了平衡的效果。排队付款一般较快,等待制作奶茶一般较慢,因此需要安排较多的制作奶茶的店员。
因此对于生产者和消费者的设计模式来说,有一点非常重要,那就是生产的速度要和消费的速度持半。如果生产得太快,而消费得太慢,那么队列会很长。面对于计算机来说,队列太长所占用的空间也会较大。
2.3 用栈实现队列
我们在前面介绍了栈和队列,以及栈和队列特殊的顺序存储结构。一些面试官会出一些题目,比如用栈实现队列和用队列实现栈。下面我们会对这两个题目进行讲解。其实这样的题目在实际工作中并不具有实际应用意义,完全是为了考察人家的思考能力。这里我们对每种数据结构及算法做相应的拓展介绍,既有利于应付面试,也有利于个人能力的提高。
2.3.1 用两个栈实现队列
栈怎样才能实现和队列一样从栈的底层抽出元素呢?一般会用两个栈来实现队列。首先,我们将两个栈分别定义为stack1与stack2。
(1)方案1
我们让入队操作在stack1中执行,而出队操作在stack2中执行。执行方式如下。
- 入队:直接向stack1中入栈。
- 出队:将stack1中的所有元素出栈,依次入栈到stack2中,然后弹出stack2中的栈顶元素,接着把stack2中的所有元素出栈,依次压入stack1中。
为了便于理解,我们借助图2-9解释上述入队操作。
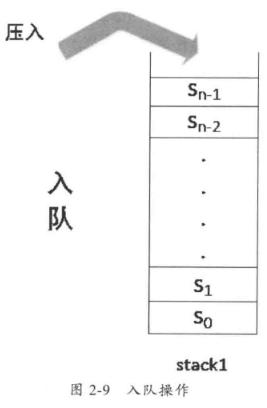
出队操作如图2-10所示。

来回入队、出队比较烦琐,尤其是出队比较麻烦,需要先将元素从stack1倒入stack2里,然后在stack2弹出元素之后又倒回到stack1里。有没有更好的办法呢?当然有,方案2就是改进之后的思路。
(2)方案2
入队都在stack1中进行,stack2用于出队,同时保证所有元素都在一个栈里,且遵守以下规则。
- 入队:不管stack1是否为空栈,都将stack2中的所有元素压入stack1中。
- 出队:若stack2不为空栈,则直接从stack2中弹出元素;若stack2为空栈,则把stack1中的元素倒入stack2中,再从stack2中弹出元素;若两个栈都是空的,则说明队列为空队,不能出队。这与方案1的思路一样,只不过把倒回去的这个操作放到了入队时执行,却使连续入队、出队的效率提高了。
还有更好的办法吗?当然有。方案3就是一种更优的解决办法。
(3)方案3
入队都在stack1中进行,出队在stack2中进行,同时遵守以下规则。
- 入队:直接把元素压入stack1中。
- 出队:如果stack2不为空,则直接弹出stack2中的元素;如果stack2为空,则将stack1中的所有元素倒入stack2中,然后弹出stack2中的栈顶元素。同样,若两个栈都为空栈,则队列为空队,无法出队。
这个方案在入队时非常简单,而在出队时,多数情况下可以直接通过出队stack2实现,若需要把stack1中的元素倒入stack2中,则一般不用每次都进行这样操作。最坏的情况就是出队一个元素、入队一个元素这样的循环操作,导致每次出队都要转移元素。
其实这三种方案的操作是一样的。总体来说,方案3是非常好的方案。
下面为方案3的代码实现。
public class Stack2Queue { private MyStack stack1; private MyStack stack2; private int maxLength; public Stack2Queue(int capacity) { maxLength = capacity * 2; stack1 = new MyStack(capacity); stack2 = new MyStack(capacity); } public boolean put(int item) { if (stack1.isFull() || maxLength == size()) { return false; } stack1.push(item); return true; } public int poll() { if (!stack2.isEmpity()) { return stack2.pop(); } else { while (!stack1.isEmpity()) { stack2.push(stack1.pop()); } return stack2.pop(); } } public int size() { return stack1.size() + stack2.size(); } }
测试代码:
public class TestStack2Queue { public static void main(String[] args) { Stack2Queue queue = new Stack2Queue(5); queue.put(1); queue.put(2); System.out.println(queue.poll());//1 queue.put(3); queue.put(4); System.out.println(queue.poll());//2 System.out.println(queue.poll());//3,本次会把3、4两个元素从stack1倒入stack2 } }
2.3.2 两个队列实现栈
下面介绍一下如何用两个队列实现栈。
栈的主要操作就是入栈和出栈,其特点就是后进先出。
我们先将两个队列分别定义为queue1与queue2。
(1)方案1
入栈和出栈,都在queue1中完成,而queue2作为中转空间。
- 入栈;直接入queue1即可。
- 出栈:把queue1中除最后一个元素外的所有元素都移动到queue2中,再将queue1中的元素出队,此时即出栈;接着将queue2中的所有元素移动到queue1中。
具体操作如图2-11和图2-12所示。
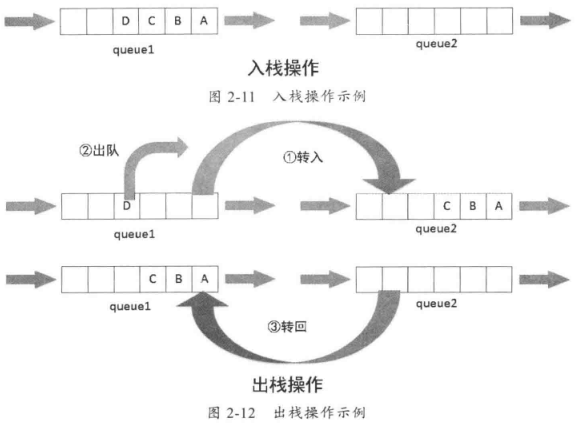
该操作过程与用栈实现队列的方案1一样,都是把第2个结构当作一个中转站,然后将数据来回倒。接下来看一个更优一点的方案。
(2)方案2
从方案1的操作方式中,我们可以看出其劣势,即在出栈时要把queue2中的元素移动到queue1中。在两个队列之间能否不用每次先出栈再把元素移动回去?当然可以。下面是入栈、出栈的具体操作描述。
- 入栈:两个队列哪个不为空,就把元素入队到哪个队列中;如果都为空,则任选一个队列入队,假设这个队列就是queue1。
- 出栈:把不为空的队列中除最后一个元素外的所有元素移动到另一个队列中,然后出队最后一个元素。
这样方案2就更简单了,省去了方案1中最后一步的转回操作。
下面是实现代码
package com.example.demo.base.queue; public class Queue2Stack { private MyArrayQueue queue1; private MyArrayQueue queue2; private int maxLength; public Queue2Stack(int capacity) { maxLength = capacity; queue1 = new MyArrayQueue(capacity); queue2 = new MyArrayQueue(capacity); } /** * 入栈 * * @param item * @return */ public boolean push(int item) { if (size() == maxLength) { return false; } if (queue2.isEmpty()) { queue1.put(item); } else { queue2.put(item); } return true; } /** * 出栈 * * @return */ public Object pop() { if (size() == 0) { throw new IndexOutOfBoundsException("栈里空了"); } else { if (queue2.isEmpty()) { while (queue1.size() > 1) { queue2.put(queue1.poll()); } return queue1.poll(); } else { while (queue2.size() > 1) { queue1.put(queue2.poll()); } return queue2.poll(); } } } public int size() { return queue1.size() + queue2.size(); } }
下面是测试代码
public class TestQueue2Stack { public static void main(String[] args) { Queue2Stack stack = new Queue2Stack(5); stack.push(1); stack.push(2); System.out.println(stack.pop());//2 stack.push(3); stack.push(4); System.out.println(stack.pop());//4 System.out.println(stack.pop());//3 } }
2.4 链表
前面有好几处提及链表,现在我们正式介绍一下。虽然在很多的高级语言中,链表已经尽量地被隐藏起来。但是其应用之处还是很多的。例如,前面介绍的散列表用链表作为解决冲突的方式及栈、队列的操作,其实都可以用链表实现。
2.4.1 什么是链表
链表与数据结构有些不同。栈和队列都是申请一段连续的空间,然后按顺序存储数据;链表是一种物理上非连续、非顺序的存储结构,数据元素之间的顺序是通过每个元素的指针关联的。
链表由一系列节点组成,每个节点一般至少会包含两部分信息;一部分是元素数据本身,另一部分是指向下一个元素地址的指针。这样的存储结构让链表相比其他线性的数据结构来说,操作会复杂一些。
与数组相比,链表具有其优势:链表克服了数组需要提前设置长度的缺点,在运行时可以根据需要随意添加元素;计算机的存储空间并不总是连续可用的,而链表可以灵活地使用存储空间,还能更好地对计算机的内存进行动态管理。
链表分为两种类型:单向链表和双向链表。我们平时说到的链表指的是单向链表。双向链表的每个节点除存储元素数据本身外,还额外存储两个指针,分别指向上一个节点和下一个节点的地址。
当然,除了这些普通的链表,链表由于其特点还衍生了很多特殊的情况,这些都会在稍后的内容中一起介绍。
2.4.2 链表的存储结构
对于链表来说,我们只需关心链表之间的关系,不需要关心链表实际存储的位置,所以在表示一个链表关系时,一般使用箭头来关联两个连续的元素节点。链表的存储结构如图2-13所示。
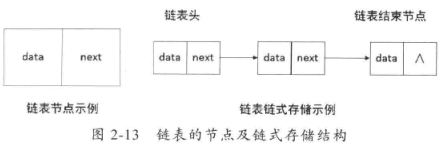
从链表的存储结构可知,链表的每个节点包含两个部分,分别是数据(叫作data)和指向下个节点地址的指针(叫作next)。在存储了一个链表之后怎么找到它?这里需要一个头节点,这个头节点是一个链表的第1个节点,它的指针指向下一个节点的地址,以此类推,直到指针指向为空时,便表示没有下一个元素了。
2.4.3 链表的操作
链表的操作有:创建、插入、删除、输出。
这里提到的插入、删除操作,其位置并不一定是开头或者结尾。由于链表特殊的存储结构,在链表中间进行数据元素的插入与删除也是很容易实现的。
创建操作就是空间的分配,把头、尾指针及链表节点数等信息初始化,这里就不详细介绍了。
在看实现代码之前,我们先通过存储结构看看链表的插入、删除是如何操作的。
1. 插入操作
插入操作分为三种情况,分别是头插入、尾插入、中间插入。
头插入的操作,实际上是增加一个新的节点,然后把新增加的节点的指针指向原来头指针指向的元素,再把头指针指向新增的节点,如图2-14所示。
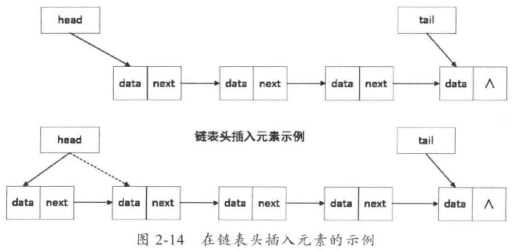
尾插入的操作,也是增加一个指针为空的节点,然后把原尾指针指向节点的指针指向新增加的节点,最后把尾指针指向新增加的节点即可,如图2-15所示(图中的虚线表示被移除的指向)。

中间插入元素的操作会稍微复杂一些。首先增加一个节点,然后把新增加的节点的指针指向插入位置的后一个位置的节点,把插入位置的前一个节点的指针指向新增加的节点即可,如图2-16所示。
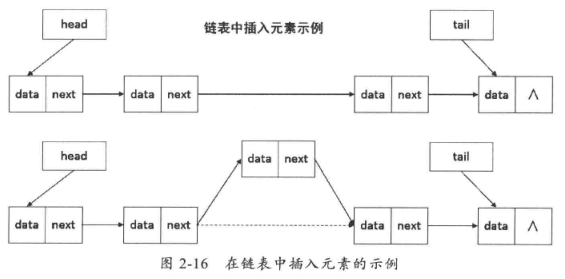
2. 删除操作
删除操作与插入操作类似,也有三种情况,分别是头删除、尾删除、中间删除。
删除头元素时,先把头指针指向下一个节点,然后把原头节点的指针置空,示意如图2-17所示。
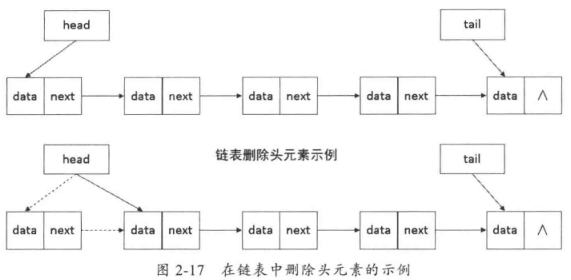
删除尾元素时,首先找到链表中倒数第2个元素,然后把尾指针指向这个元素,接着把原倒数第2个元素的尾指针置空,如2-18所示。

删除中间元素时会相对复杂一些,首先把要删除的节点的之前一个节点的指针指向要删除的节点的下一个节点,接着把要删除节点的指针置空,如图2-19所示。
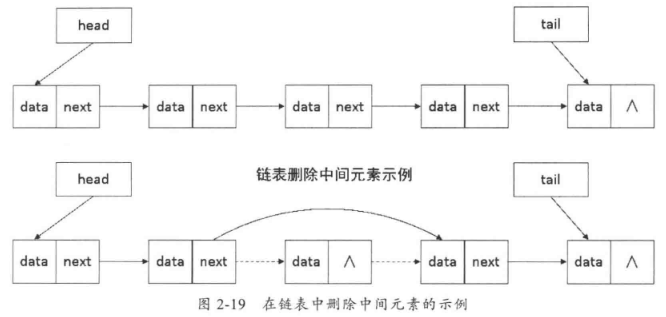
程序代码如下。链表需要两个部分的实现:节点和链表。首先是节点部分的代码。
package com.example.demo.base.link; public class MyNode { private int data; private MyNode next; public int getData() { return data; } public void setData(int data) { this.data = data; } public MyNode getNext() { return next; } public void setNext(MyNode next) { this.next = next; } }
节点的代码实现了两个部分,一个是数据,一个是指向下一个节点的属性(这里用了这个类本身作为下一个元素的类型,这应该很好理解)。
下面是链表的代码实现。
package com.example.demo.base.link; public class MyLink { private int size = 0; private MyNode first; private MyNode last; /** * 链表初始化 */ public MyLink() { } /** * 链表尾部插入 * * @param data */ public void addLast(int data) { if (size == 0) { // 为空初始化前后元素 fillStart(data); } else { MyNode node = new MyNode(); node.setData(data); last.setNext(node); last = node;// 把最后插入的元素设置为链表尾的元素 } size++; } /** * 链表头部插入 * * @param data */ public void addFirst(int data) { if (size == 0) { // 为空初始化前后元素 fillStart(data); } else { MyNode node = new MyNode(); node.setData(data); node.setNext(first);// 把元素的下一个位置的指针指向头元素 first = node;// 把刚插入的元素设置为链表头元素 } size++; } /** * 在链表指定的位置后面插入 * * @param data * @param index */ public void add(int data, int index) { if (size > index) { if (size == 0) { // 为空初始化前后元素 fillStart(data); size++; } else if (index == 0) { addFirst(data); } else if (size == index + 1) { addLast(data); } else { MyNode temp = get(index); MyNode node = new MyNode(); node.setData(data); node.setNext(temp.getNext()); temp.setNext(node); size++; } } else { throw new IndexOutOfBoundsException("链表没有那么长"); } } /** * 删除链表头元素 */ public void removeFirst() { if (size == 0) { throw new IndexOutOfBoundsException("链表没有元素了"); } else if (size == 1) { // 只剩一个元素了清除first和last clear(); } else { MyNode temp = first; first = temp.getNext(); temp = null;// 把空间回收 size--; } } /** * 删除链表尾元素 */ public void removeLast() { if (size == 0) { throw new IndexOutOfBoundsException("链表没有元素了"); } else if (size == 1) { // 只剩一个元素了清除first和last clear(); } else { MyNode temp = get(size - 2); temp.setNext(null);// 把空间回收 size--; } } /** * 删除链表中间元素 * * @param index */ public void removeMiddle(int index) { if (size == 0) { throw new IndexOutOfBoundsException("链表没有元素了"); } else if (size == 1) { // 只剩一个元素了清除first和last clear(); } else { if (index == 0) { removeFirst(); } else if (size == index - 1) { removeLast(); } else { MyNode temp = get(index - 1);// 获取要删除的元素之前的一个元素 MyNode next = temp.getNext(); temp.setNext(next.getNext()); next = null;// 把空间回收 size--; } } } /** * 打印所有元素的数据 */ public void printAll() { // 当然,也可以用 do...while 实现 MyNode temp = first; System.out.println(temp.getData()); for (int i = 0; i < size - 1; i++) { temp = temp.getNext(); System.out.println(temp.getData()); } } /** * 获取指定下标元素 * * @param index * @return */ public MyNode get(int index) { MyNode temp = first; for (int i = 0; i < index; i++) { temp = temp.getNext(); } return temp; } /** * 在链表中插入第1个元素时,头、尾元素都是一个元素 * * @param data */ private void fillStart(int data) { first = new MyNode(); first.setData(data); last = first; } /** * 在元素只有一个时清除first和last元素 */ private void clear() { first = null; last = null; size = 0; } public int size() { return size; } }
下面是测试代码
package com.example.demo.base.link; public class TestMyLink { public static void main(String[] args) { MyLink link = new MyLink(); link.addFirst(2); link.addFirst(1); link.addLast(4); link.addLast(5); link.add(3, 1);// 在下标为1的元素之后插入元素 printAllElements(link);// 1,2,3,4,5 link.printAll();// 这样打印效率会更高 link.removeFirst(); link.removeLast(); link.removeMiddle(1); printAllElements(link);// 移除了头尾之后,剩下3个元素,移除下标为1的元素,剩下两个元素2和4 link.removeFirst(); link.removeFirst(); System.out.println(link.size());// 从头部全部移除 } private static void printAllElements(MyLink link) { for (int i = 0; i < link.size(); i++) { System.out.println(link.get(i).getData()); } } }
链表的实现逻辑有点复杂。在程序中可以看到有抛出异常的情况,在中间插入和删除也考虑到index为头和尾的情况,这样避免调用方法失误而导致程序出错。
2.4.4 链表的特点
链表由于本身存储结构的原因,有以下几个特点。
(1)物理空间不连续,空间开销更大。
链表最大的一个特点是在物理空间上可以不连续。这样的优点是可以利用操作系统的动态内存管理,缺点是需要更多的存储空间去存储指针信息。
(2)在运行时可以动态添加。
由于数组需要在初始化时设定长度,所以在使用数组时往往会出现长度不够的情况,这时只能再声明一个更长的数组,然后把旧数组的数据复制进去,在前面栈的实现中已经看到了这一点。但是若使用链表,则一般不会出现空间不够用的情况。
(3)查找元素需要顺序查找
通过上面的代码可以看出,查找元素时,需要逐个遍历往后查找元素。其实在测试代码中采用循环队列元素的方法的效率并不高,尤其是当链表很长时,所查找的元素的位置越靠后,效率越低。
在执行删除操作时,也会遇到类似的问题。
(4)操作稍显复杂
在增加和删除元素时,不但需要处理数据,还需要处理指针。从代码来看,删除最后一个元素时,获取最后一个元素很方便,但是由于操作需要实现倒数第2个元素的next指向设置为空,所以只能从头遍历并获取倒数第2个元素之后再进行删除操作。
2.4.5 链表的适用场景
现在,计算机的空间越来越大,物理空间的开销已经不是我们要关心的问题了,运效率才是我们在开发中主要考虑的问题。
我们在前面提到,链表除了单向链表,还有双向链表。一般我们会优先使用双向链表,因为多使用的那个指针所占用的空间对于现在的计算机资源来说并不重要。双向链表相对于单向链表的一个优势就是,不管是从头找还是从尾找,操作是一样的。因此对尾元素进行操作时就不用逐个从头遍历了,可以直接从尾向前查找元素。
链表可以在运行时动态添加元素,这对于不确定长度的顺序存储来说很重要。在第1章中介绍的集合(列表)采用数组实现,在空间不够时需要换个更大的数组,然后进行数据复制操作。这时如果采用链表就非常方便了。
链表有什么劣势?劣势就是在查找中间元素时需要遍历。一般而言,链表也经常配合其他结构一同使用,例如散列表、栈、队列等。
一般的程序里可能会使用一个简单的队列进行消息缓冲,而队列的操作只能从头、尾进行,所以此时使用表(双向链表)去实现就非常方便。
如果有兴趣,则可以尝试自已实现一下链表版的队列。
2.4.6 链表的性能分析
一般我们在分析性能时都是以单向链表作为分析对象的。
链表的插入分为三种:头插、尾插和中间插。头、尾插是能够直接插入的,其时间复杂度为O(1);而中间插需要遍历链表,所以时间复杂度为O(L),L为插入下标。
链表的删除同样也分为三种:头删、尾删和中间删。头删的时间复杂度为O(1);中间同样是O(L),尾删的时间复杂度则达到了O(N),N为链表长度。
对于查询来说,时间复杂度是O(L),L为查询下标。
所以对于链表来说,我们可以发现,链表的头插和头删都是O(1)的时间复杂度,这和栈很像,所以栈可以直接使用单向链表实现。
2.4.7 面试举例:如何反转链表
怎么反转链表呢?这个是面试中经常出现的一道题。一般在数据结构或者算法的面试题中,尽量不使用额外的空间去实现,尽管现在的计算机空间很充足,但是面试考察的还是对于整体性能的考虑。
方法其实有很多,我们可以依次遍历链表,然后依次使用头插入的方法来达到目的。
其中有个简单的方法,就是把链表的每个指针反转。
下面就是通过反转指针来实现反转链表的代码。
/** * 翻转链表 */ public void reverse() { MyNode temp = first; last = temp; MyNode next = first.getNext(); for (int i = 0; i < size - 1; i++) { MyNode nextNext = next.getNext();// 下下个 next.setNext(temp); temp = next; next = nextNext; } last.setNext(null); first = temp; }
这部分代码应该在 MyLink 类里,通过反转指针实现链表反转。接下来我们看看测试代码。
package com.example.demo.base.link; public class TestMyLink { public static void main(String[] args) { MyLink link = new MyLink(); link.addLast(1); link.addLast(2); link.addLast(3); link.addLast(4); printAllElements(link); link.reverse(); printAllElements(link); } private static void printAllElements(MyLink link) { for (int i = 0; i < link.size(); i++) { System.out.println(link.get(i).getData()); } } }
这样可以轻松地完成链表反转。


