python的竞争性学习模型尝试

很多时候决定一个决策好不好，需要模拟之后来看后果

决策不好的，在环境中自然就不能生存

以下是通过制作一个竞争性学习的模型，来模仿一些决策行为

决策

博弈有三个要素：参与者、策略与利益
不同的策略带来不同的利益
各个参与者都尽可能的选择为自己带来最高的利益的决策
在研究博弈论时，参与者还会假设其他参与者都会选择为自己带来最高的利益的决策
但是现实生活中不是每个人都像柯南那么聪明，也不是每个人都像开司那样赌术精湛
所以在工作中研究类似过程的时候，除了采用经济学理论来证明
我尝试建立一个竞争性学习的模型
以“优胜劣汰”的形式，为每个机器人设定生命值
每个回合让机器人之间互相进行决策，决策最后获得的利益影响他们的生命值
每个回合结束后会有更新机制，淘汰一部分机器人，新增新的机器人
根据生命值的多少程度决定是否是要淘汰
新增的机器人采用生命值最高的机器人，继承这些机器人的策略并且在小范围内做微调
重复多个回合，最后观察机器人之间的策略选择倾向
以下采用囚徒困境来验证一个竞争性学习模型
囚徒困境可以归纳成一个两个玩家参加的游戏
这两个玩家不可以互相沟通，可以选择以下两个策略：举报对方或不举报

如果两者都举报的，各判8年

如果一个举报而另外一个不举报的，举报那个仅判1年，不举报的判10年

如果两者都不举报，均当场释放

这两个玩家的不同策略与收益可以视为以下的矩阵

-	举报	不举报
举报	(-8,-8)	(-1,-10)
不举报	(-10,-1)	(0,0)

这个博弈的关键点在于：

在全局角度看（帕累托最优），应该双方都选择不举报

但是在各自的角度看，选择举报才是最合理的

如果对方举报，我举报了受的伤害更小(-8<-10)

如果对方不举报，我举报了我也是受到的伤害更小 (-1<0)

这个博弈也是博弈论的经典问题

以这个开始制作竞争性学习模型

代码

#导入包
import pandas as pd
import numpy as np
from random import random,sample
from matplotlib import pyplot as plt

#多个机器人之间互相配对的函数，给个随机列，然后排序，两两组队
def pairing(robotDict):
    dfQueue=pd.DataFrame([{'id':i,'r':random()} for i in robotDict.keys() if robotDict[i]['alive']]).sort_values(by='r')
    pairQueue=[]
    for i in range(0,len(dfQueue),2):
        try:
            pairQueue.append((dfQueue.iloc[i]['id'],dfQueue.iloc[i+1]['id']))
        except:
            continue
    return pairQueue

HP=0  #初始的生命值，生命值允许存在负数，越低的生命值就越有可能淘汰
n=50000
turnover=5000  #每个回合淘汰人数
#创建n个机器人，每个机器人设置一个生命值hp，默认生命值是HP，开始初始化，对于不同策略的喜好也初始化
robotDict={}
for i in range(n):
    robotDict[i]={'hp':HP,'tend':random(),'alive':True,'startRound':0,'endRound':0}

roundMax=50
for r in range(roundMax):
    #开始经历回合，每个回合，机器人之间互相配对
    pairQueue=pairing(robotDict)
    #开始竞争，根据每个机器人的tend，设定每个机器人的应有策略，根据策略调整机器人的hp，每个回合重复50次博弈
    for i in range(50):
        for (robotId0,robotId1) in pairQueue:
            move0=random()>robotDict[robotId0]['tend']  #是否举报
            move1=random()>robotDict[robotId1]['tend'] #是否举报
            if move0 and move1:
                robotDict[robotId0]['hp']-=8
                robotDict[robotId1]['hp']-=8
            elif not move0 and move1:
                robotDict[robotId0]['hp']-=10
                robotDict[robotId1]['hp']-=1
            elif move0 and not move1:
                robotDict[robotId1]['hp']-=10
                robotDict[robotId0]['hp']-=1
            else:
                robotDict[robotId0]['hp']-=0
                robotDict[robotId1]['hp']-=0
    #每回合结束后：淘汰生命值最低的turnover个机器人
    dfTmp=pd.DataFrame(robotDict).T.sort_values(by='hp')
    killSet=set(dfTmp[dfTmp['alive']].iloc[:turnover,:].index)
    for robotId in killSet:
        robotDict[robotId]['alive']=False
    #以生命值最高的turnover个机器人为蓝本，产生新的机器人，新的机器人继承旧机器人的tend并且稍加变化
    burnSet=set(dfTmp[dfTmp['alive']].iloc[-turnover:,:].index)
    for robotId in burnSet:
        robotDict[len(robotDict)]={'hp':0,'tend':robotDict[robotId]['tend']+0.001*random(),'alive':True,'startRound':r,'endRound':r}
    #对所有机器人重新设定生命值，对于还没有挂的，endRound+1
    for robotId in robotDict.keys():
        if robotDict[robotId]['alive']:
            robotDict[robotId]['hp']=0
            robotDict[robotId]['endRound']+=1

训练结果

第0个回合，每个机器人的策略分布是从0到1的随机均匀分布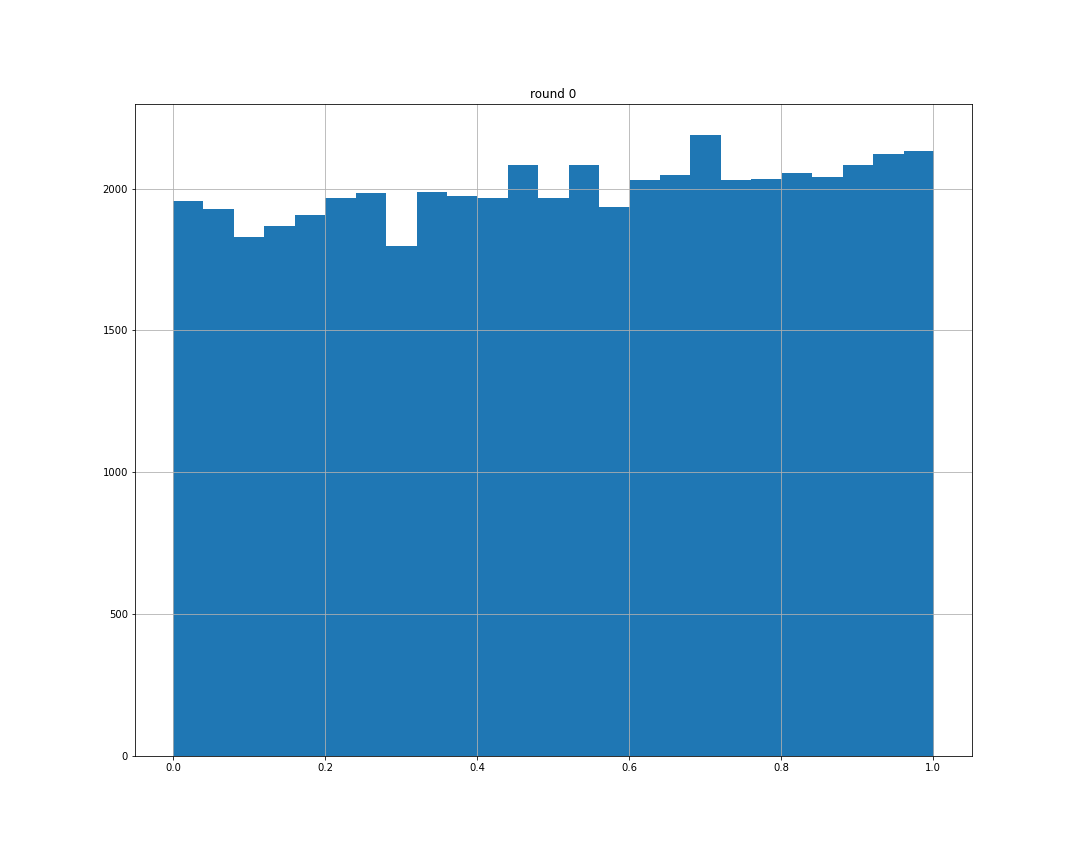

第99个回合（最后一个回合），每个机器人的策略分布如下

对tend每0.2划分一个区间，行程5个策略态度种类，每个测量态度的机器人存活数量变化如下

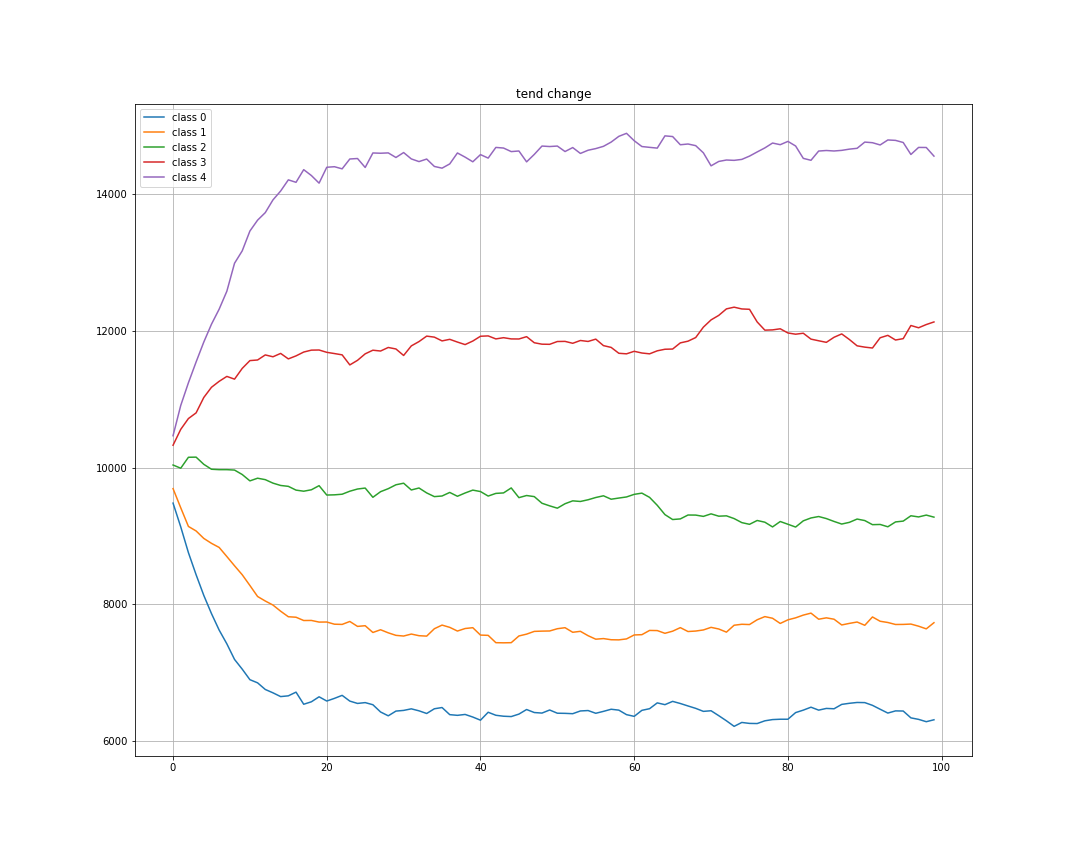
从结果图可以看出，最后是举报的机器人存活的较多，不举报的基本被淘汰，符合理论预期。