数据散布度量（下）

四、MAD实际应用的例子

光说不练假把式。
我们用实际案例来了解一下MAD。
假设，我们处于这样一个应用场景：
我们需要做meta分析，采集了1000个人在住院期间进行各种治疗的数据。
有些治疗仅持续了几天（临时医嘱），有些药物持续了整个住院期间（长期医嘱）。
怎么样判断这些治疗是临时医嘱还是长期医嘱？
我们可以把这个问题等价为，在疗程内每一天治疗的人数构成了一个分布，需要描述这个分布是集中的（临时医嘱）还是散布的（长期医嘱）。
我们模拟不同的单尾正态分布来模拟出不同治疗可能出现的效果，并且计算各自的MAD。

from scipy import stats
import pandas as pd
c=0

#实际情况
case_count=1000  #采集样本数
period=9  #疗程
mean=0  #峰值所在日期
std=3  #分布标准差

#生成画布与坐标轴
fig,axs=plt.subplots(nrows=4,ncols=3)
fig.set_size_inches((22,12))

#对不同的分布标准差来判断
for std in np.linspace(0.2,20,12):
    
    case_count=1000  #采集样本数
    period=15  #疗程
    mean=0  #峰值所在日期
    
    #峰值所在天的Θ值
    theta0=stats.norm.cdf(mean+1, mean, std)-stats.norm.cdf(mean, mean, std)
    
    #坐标轴所在的行号与列号
    row=c//3
    col=c%3
    
    ax=axs[row,col]
    used_list=[]
    for i in range(period):
        #从i天到i+1天的概率累积值，代表了那一天可能服用药物的概率，乘以样本数量即为服用药物的人数
        thetai=stats.norm.cdf(i+1, mean, std)-stats.norm.cdf(i, mean, std)
        used_count=int(thetai/theta0*case_count)  
        used_list.append(used_count)

    drug_count=np.array(used_list).sum()

    #中位天数：先计算每一天的使用数量的累积求和，然后切出累积求和小于或等于样本数一半的那一部分，那一部分的数组长度-1就等于天数中位数
    median=np.array(used_list).cumsum()[np.array(used_list).cumsum()<=drug_count/2].shape[0]-1
    if median<0:
        median=0

    #MAD：（每一个样本的使用天数与中位天数的差）的中位数，借助dataframe计算中位数残差median_dev的累积求和并排序，然后操作同上
    df=pd.DataFrame({'median_dev':abs(np.array(range(period))-median),'used_count':used_list}).sort_values(by='median_dev')
    df['cumsum']=df['used_count'].cumsum()
    if len(df[df['cumsum']<=drug_count/2]['median_dev'])>0:
        MAD=df[df['cumsum']<=drug_count/2]['median_dev'].iloc[-1]
    else:
        MAD=0

    ax.bar(range(period),used_list,label='std=%.2f,MAD=%d'%(std,MAD))
    ax.grid()
    ax.legend()
    c+=1

fig.tight_layout()

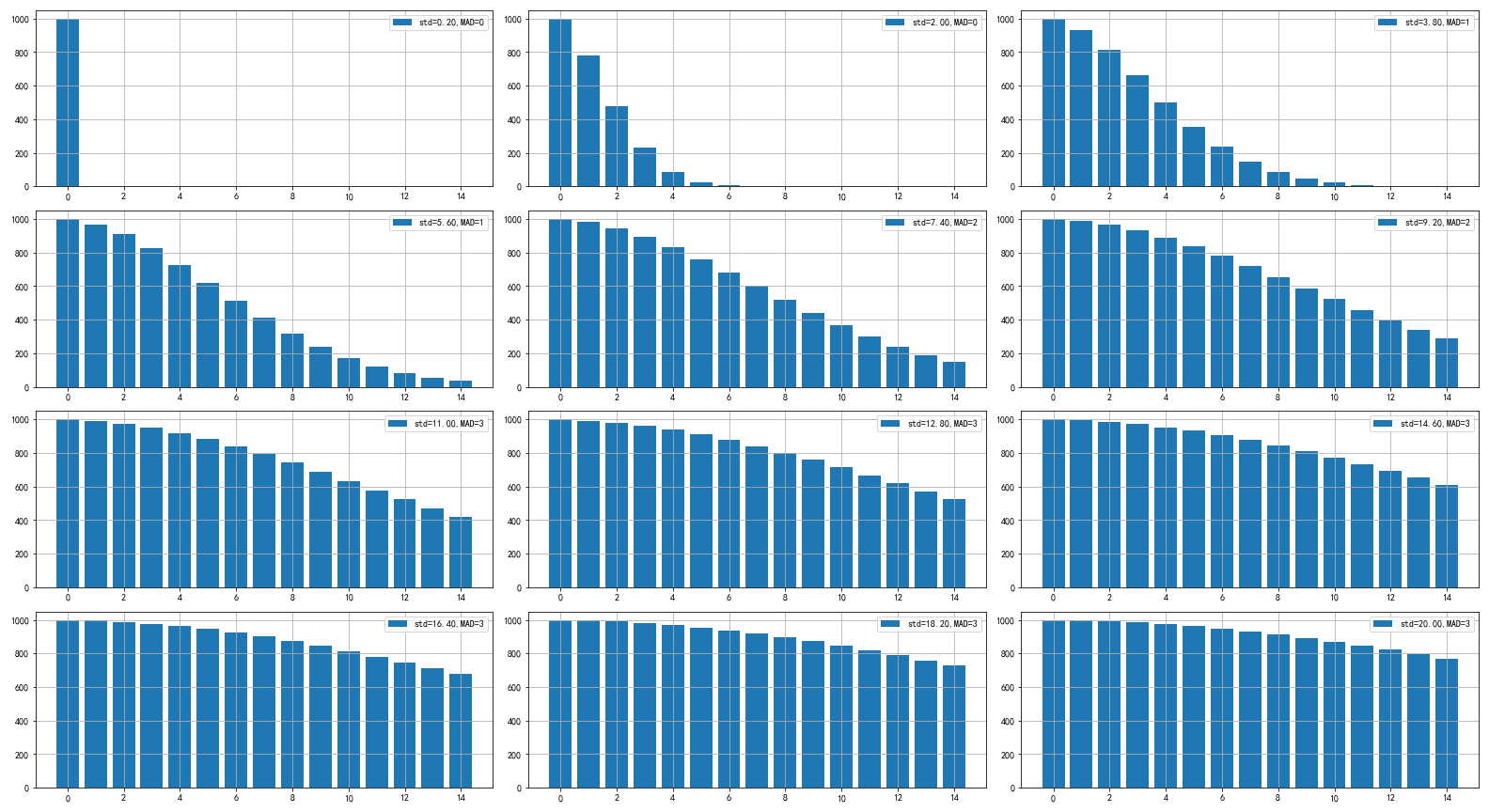
从图上可以看出，当标准差<3的时候，MAD<0，分布集中，这个时候可以视为这种治疗是属于临时医嘱。
理论上，period越高，需要的标准差越低，但是经过计算，标准差都在3左右。
如果均值不在两端，则需要的标准差应该要更低。不同的疗程市场、不同的均值的影响大概如下。

#实际情况
case_count=1000  #采集样本数
period=9  #疗程
mean=0  #峰值所在日期
std=3  #分布标准差

period_list=range(5,30)
std_list=np.linspace(0.1,20,100)
std_result_list=np.zeros(shape=(3,len(period_list)))

#生成画布与坐标轴
fig,axs=plt.subplots(nrows=1,ncols=2)
fig.set_size_inches((22,6))

#对不同的疗程时长、不同的分布标准差来判断
#对不同的分布标准差来判断
ax=axs[0]
is_break=False
for index,period in enumerate(period_list):
    for std in std_list:

        case_count=1000  #采集样本数
        mean=0  #峰值所在日期

        #峰值所在天的Θ值
        theta0=stats.norm.cdf(mean+1, mean, std)-stats.norm.cdf(mean, mean, std)

        used_list=[]
        for i in range(period):
            #从i天到i+1天的概率累积值，代表了那一天可能服用药物的概率，乘以样本数量即为服用药物的人数
            thetai=stats.norm.cdf(i+1, mean, std)-stats.norm.cdf(i, mean, std)
            used_count=int(thetai/theta0*case_count)
            used_list.append(used_count)

        drug_count=np.array(used_list).sum()

        #中位天数：先计算每一天的使用数量的累积求和，然后切出累积求和小于或等于样本数一半的那一部分，那一部分的数组长度-1就等于天数中位数
        median=np.array(used_list).cumsum()[np.array(used_list).cumsum()<=drug_count/2].shape[0]-1
        if median<0:
            median=0

        #MAD：（每一个样本的使用天数与中位天数的差）的中位数，借助dataframe计算中位数残差median_dev的累积求和并排序，然后操作同上
        df=pd.DataFrame({'median_dev':abs(np.array(range(period))-median),'used_count':used_list}).sort_values(by='median_dev')
        df['cumsum']=df['used_count'].cumsum()
        if len(df[df['cumsum']<=drug_count/2]['median_dev'])>0:
            MAD=df[df['cumsum']<=drug_count/2]['median_dev'].iloc[-1]
        else:
            MAD=0
        
        #如果MAD大于0，则停止，记录下对应的std
        if MAD<=2:
            std_result_list[MAD,index]=std
std_result_list[std_result_list==0]=np.nan
for i in range(3):
    ax.plot(period_list,std_result_list[i],label='MAD=%d'%(i))
ax.grid()
ax.legend()
ax.set_xlabel('period疗程时长')
ax.set_ylabel('std标准差')

#对疗程市场为9天、不同的峰值所在日期、不同的分布标准差来判断
#对不同的分布标准差来判断
ax=axs[1]
mean_list=range(0,16)
std_result_list=np.zeros(shape=(3,len(mean_list)))
for mean in mean_list:
    for std in std_list:

        case_count=1000  #采集样本数
        period=15  #峰值所在日期

        #峰值所在天的Θ值
        theta0=stats.norm.cdf(mean+1, mean, std)-stats.norm.cdf(mean, mean, std)

        used_list=[]
        for i in range(period):
            #从i天到i+1天的概率累积值，代表了那一天可能服用药物的概率，乘以样本数量即为服用药物的人数
            thetai=stats.norm.cdf(i+1, mean, std)-stats.norm.cdf(i, mean, std)
            used_count=int(thetai/theta0*case_count)
            used_list.append(used_count)

        drug_count=np.array(used_list).sum()

        #中位天数：先计算每一天的使用数量的累积求和，然后切出累积求和小于或等于样本数一半的那一部分，那一部分的数组长度-1就等于天数中位数
        median=np.array(used_list).cumsum()[np.array(used_list).cumsum()<=drug_count/2].shape[0]-1
        if median<0:
            median=0

        #MAD：（每一个样本的使用天数与中位天数的差）的中位数，借助dataframe计算中位数残差median_dev的累积求和并排序，然后操作同上
        df=pd.DataFrame({'median_dev':abs(np.array(range(period))-median),'used_count':used_list}).sort_values(by='median_dev')
        df['cumsum']=df['used_count'].cumsum()
        if len(df[df['cumsum']<=drug_count/2]['median_dev'])>0:
            MAD=df[df['cumsum']<=drug_count/2]['median_dev'].iloc[-1]
        else:
            MAD=0
        
        #如果MAD大于0，则停止，记录下对应的std
        if MAD<=2:
            std_result_list[MAD,mean]=std
std_result_list[std_result_list==0]=np.nan
for i in range(3):
    ax.plot(mean_list,std_result_list[i],label='MAD=%d'%(i))
ax.grid()
ax.legend()
ax.set_xlabel('mean峰值所在日期')
ax.set_ylabel('std标准差')
fig.tight_layout()

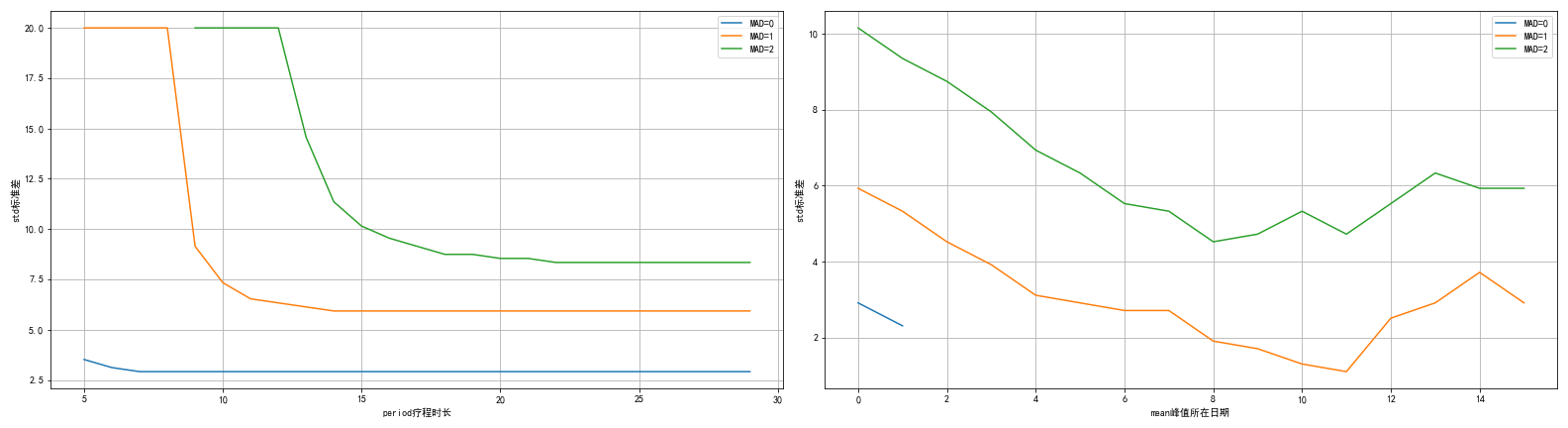
从上图可看出
其实由于MAD的定义，易见，设疗程为period，有以下集中情况：

1. 如果仅仅有疗程第一天(x=0)的时候有使用治疗，其余时间都没有使用治疗，这时候就是典型的临时医嘱，MAD=0。
2. 如果每一天都有使用治疗，这时候就是典型的长期医嘱，MAD=int(int(period/2)/2)。
3. 如果仅仅有疗程第一天(x=0)还有疗程最后一天(x=period)的时候有使用治疗，其余时间都没有使用治疗，这时候就是特别的临时医嘱，即入院第一天跟出院当天需要使用治疗，这时候MAD达到理论上的最大值，MAD=int(period/2)。

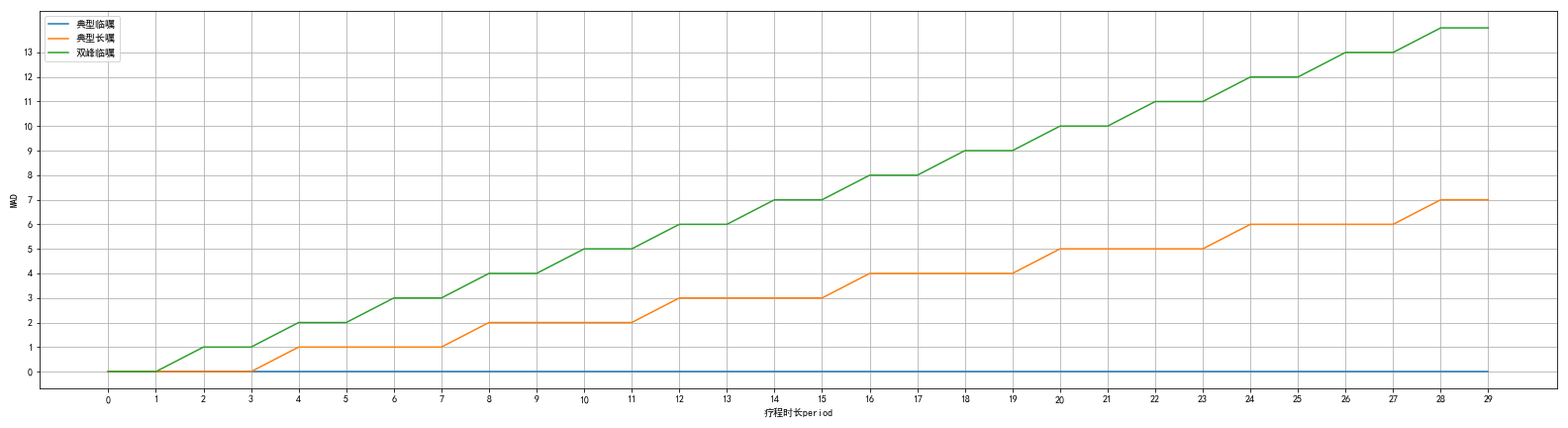
所以对于判定这项治疗属于哪一种形式，可以以0，int(int(period/2)/2)，int(period/2)这三个时间节点来衡量。
不同的疗程时长所对应的三个时间节点如图。