Shader学习08【法线变换】

法线变换：

在了解shader所需要的数学知识的最后，我们来看一种特殊的变换：法线变换

法线（normal），也被称为法矢量（normal vector），在上面我们已经看到如何使用变换矩阵来变换一个顶点或一个方向矢量，但法线是需要我们特殊处理的一种方向矢量，在游戏中，模型的一个顶点往往会携带额外的信息，而顶点法线就是其中一种信息，当我们变换一个模型的时候，不仅需要变换它的顶点，还需要变换顶点法线，以便在后续处理（如片元着色器）中计算光照等。

一般来说，点和绝大部分方向矢量都可以使用同一个4*4或3*3的变换矩阵M_a->b把其从坐标空间A变换到坐标空间B中，但在变换法线的时候，如果使用同一个矩阵，可能就无法确保维持发现的垂直性，先来看一下为什么会出现这样的问题：

先了解一下另一种方向矢量——切线（tangent），也被称为切矢量（tangent vector）。与法线类似，切线往往也是模型顶点携带的一种信息，它通常与纹理空间对齐，而且与法线方向垂直：

 

由于切线是由两个顶点之间的差值计算得到的，因此我们可以直接使用用于变换顶点的变换矩阵来变换切线，假设，我们使用3*3的变换M_a->b来变换顶点（注意下，这里设计的变换矩阵都是3*3的矩阵，不考虑平移变换。这是因为切线和法线都是方向矢量，不会受平移的影响），可以由下面的式子直接得到变换后的切线

 

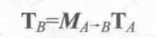
其中Ta和Tb分别表示在坐标空间A下和坐标空间B下的切线方向，但如果直接使用M_a->b来变换发现，得到的新法线方向可能就不会与表面垂直了，下图给出了一个例子

 

 

那么应该使用哪个矩阵来变换法线呢？我们可以由数学约束条件来推出这个矩阵，我们知道同一个顶点的切线Ta和法线Na必须满足垂直条件，即Ta*Na=0。给定变换矩阵MA->B，我们已经知道TB=MA->B*TA。我们现在想要找到一个矩阵G来变换法线NA，使得变换后的法线仍然与切线垂直，即T_B*N_B=(M_A->BT_A)*(GN_A)=0

对上式进行一些推导后得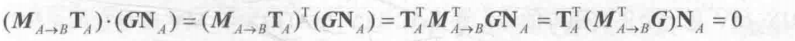

由于 T_A*N_A=0，因此如果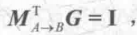，那么上式成立，也就是说，如果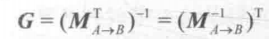，即使使用原变换矩阵的逆转置矩阵来变换法线就可以得到正确的结果。

 

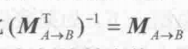值得注意的是，如果变换矩阵M_A->B是正交矩阵，，因此，也就是说我们可以使用用于变换顶点的变换矩阵来直接变换法线。如果变换只包括旋转变换，那么这个变换矩阵就是正交矩阵，而如果变换只包含旋转和统一缩放，我们利用统一缩放系数k来得到变换矩阵M_A->B逆转置矩阵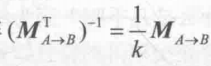。这样就可以避免计算逆矩阵的过程，如果变换中包含了非同一变换，那么我们就必须要求求解逆矩阵来得到变换法线的矩阵。