Shader学习05【矩阵变换】
非常重要的一节!
前言:我们看到了一个矩阵可以理解自己看到了一个变换,在游戏的世界中,这些变换一般包含了旋转,缩放,平移。游戏开发人员希望给定一个点或矢量,再给定一个变换(例如把点平移到另一个位置,把矢量的方向旋转30度等等),就可以通过某个数学运算来求得新的点和矢量。聪明的先人们发现,可以使用矩阵来完美解决这个问题,那么问题就变成了,我们如何使用矩阵来表示这些变换
1:什么是变换
变换(transform),指的是我们把一些数据,如点,方向矢量甚至是颜色等,通过某种方式进行转换的过程。在计算机图形学领域,变换非常重要,尽管通过变换我们能够进行的操作是有限的,但这些操作已经足够奠定变换在图形学领域举足轻重的位置了
首先来看一个非常简单的变换类型——线性变换(linear transform)。线性变换指的是那些可以保留矢量加和标量乘的变换。用数学公式来表示这两个条件就是:
f(x)+f(y)=f(x+y),kf(x)=f(kx)
上面的公式看起来过于抽象,缩放(scale)就是一种线性变换,例如,f(x)=2x,可以表示一个大小为2的统一缩放,即经过变换后矢量的x的模被放大两倍,可以发现,f(x)=2x是满足上面的两个条件的,同样,旋转(rotation)也是一种线性变换,对于线性变换来说,如果我们要对一个三维的矢量进行变换,那么仅仅使用3*3的矩阵就可以表示所有的线性变换
线性变换除了包括旋转和缩放以外,还包括错切(shear) ,镜像(mirroring),也被称为reflection,正交投影(orthographic projection)等,这里着重看一下旋转和缩放变换
但是,仅有线性变换是不够的,我们来考虑平移变换,例如f(x)=x+(1,2,3),这个变换就不是一个线性变换,它满足标量乘法,但不满足矢量加法,如果我们令x=(1,1,1),那么:
f(x)+f(y)=(4,6,8)
f(x+x)=(3,4,5)
可见,两个运算结果是不一样的,因此,我们不能用一个3*3的矩阵来表示一个平移变换,这是我们不希望看到的,毕竟平移变换是非常常见的一种变换。
看到这里读者可能已经对所谓线性变换的理解产生了分歧和不解,这里给出博客链接,整理了关于矩阵和线性变换的内容。
https://www.cnblogs.com/justkillthree/articles/14821600.html
由于平移变换不是线性变换,所以我们又有了仿射变换,仿射变换就是合并线性变换和平移变换的变换类型,仿射变换可以用一个4*4的矩阵来表示,为此,我们需要把矢量扩展到四维空间下,这就是齐次坐标空间(homogeneous space)
下图给出了图形学中常见变换矩阵的名称和它们的特性

在下面的内容里,将会讲到一些基本的变换类型,旋转,缩放,平移。对于正交投影和透视投影,将在后续内容中给出表示方法。
2:齐次坐标
通过上述内容,我们知道,3*3矩阵是不能表示平移操作的,我们将其扩展到了4*4的矩阵(只要多一个维度就可以实现对平移的表示),为此,我们还需要把原来的三维矢量转换成四维矢量,也就是我们所说的齐次坐标(homogeneous coordinate)(事实上齐次坐标的维度可以超过四维,但本书中所说的齐次坐标将泛指四维齐次坐标),我们可以发现,齐次坐标并没有神秘的地方,它只是为了方便计算而使用的一种表示方式而已
如上,齐次坐标是一个四维矢量。那么,我们如何把三维矢量转换成齐次坐标呢?对于一个点,从三维坐标转换成齐次坐标是把其w分量设为1,而对于方向矢量来说,需要把其w分量设为0。这样的设置会导致当用一个4*4矩阵对一个点进行变换时,平移,旋转,缩放都会施加于该点,但是如果是用于变换一个方向矢量,平移的效果就会被忽略,下面讲解其原因
3:分解基础变换矩阵
我们已经知晓,可以使用一个4*4的矩阵表示平移,旋转和缩放。我们表示把纯平移,纯旋转和纯缩放的变换矩阵叫做基础变换矩阵,这些矩阵具有一些共同点,我们可以把一个基础变换矩阵分解成4个组成部分:
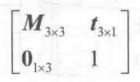
其中,左上角的矩阵M3*3用于表示旋转和缩放,t3*1用于表示平移,01*3是零矩阵,右下角的元素就是标量1
接下来,我们来具体学习如何使用这样一个4*4的矩阵来表示平移,旋转,和缩放
4:平移矩阵
我们可以使用矩阵乘法来表示对一个点进行平移变换
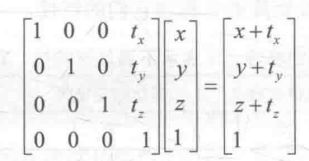
从结果来看,非常容易理解为什么四维矩阵具有平移的效果,点x,y,z分量分别增加的位移给到了另一个维度上,有趣的是如果我们对一个方向矢量进行平移变换,结果如下:
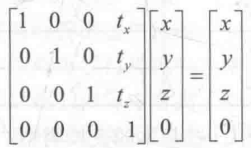
可以发现,平移变换不会对方向矢量产生任何影响,这点很容易理解,我们在学习矢量的时候就说过了,矢量没有位置属性,也就是说它可以位于空间中的任意一点,因此对位置的改变(即平移)不会对四维矢量产生影响
现在,应该明白当给定一个平移操作时如何构建一个平移矩阵,基础变换矩阵中的t3*1矢量对应了平移矢量,左上角的矩阵M3*3为单位矩阵I3,平移矩阵的逆矩阵就是反向平移得到的矩阵,即
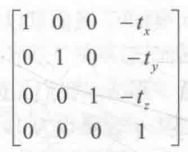
可以看出,平移矩阵并不是一个正交矩阵
5:缩放矩阵
我们可以对一个模型沿空间的x轴,y轴,z轴进行缩放。同样,可以使用一个旋转矩阵来表示一个缩放变换

对方向适量可以使用同样的矩阵进行缩放

如果缩放系数kx=ky=kz,我们把这样的缩放称为统一缩放(uniform scale)否则称为非统一缩放(nonuniform scale)。从外观上看,统一缩放是扩大整个模型,而非统一缩放会拉伸或挤压模型,更重要的是,统一缩放不会改变角度和比例信息,而非统一缩放会改变与模型有关的角度和比例,例如,在对法线进行变换时,如果存在非统一缩放,直接使用用于变换顶点的变换矩阵的话,就会得到错误的结果,正确的变换方法可参见4.7节
缩放矩阵的逆矩阵是使用原缩放系数的倒数来对点或方向矢量进行缩放,即

缩放矩阵一般不是正交矩阵。
上面的矩阵是适用于沿坐标轴方向进行缩放,就需要使用一个复合变换,其中一个方法的主要思想就是,先将缩放轴变换成标准坐标轴,然后进行沿坐标轴的缩放,再使用逆变换得到原来的缩放轴的朝向。
6:旋转矩阵
旋转是三种常见的变换矩阵中最复杂的一种。我们知道,旋转操作需要指定一个旋转轴,这个旋转轴,不一定是空间中的坐标轴,但下面主要探究围绕空间中的X轴Y轴Z轴进行旋转
如果我们需要把点绕着X轴旋转Θ度,可以使用下面的矩阵:
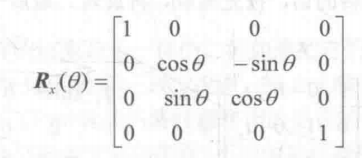
绕Y轴的旋转也是类似的:
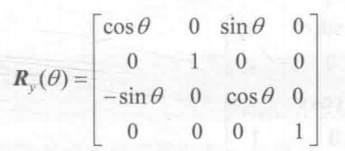
最后是绕Z轴的旋转:
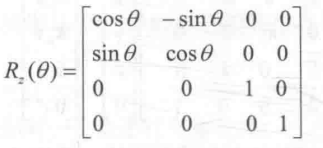
旋转矩阵的逆矩阵是旋转相反角度得到的变换矩阵,旋转矩阵是正交矩阵,而且多个旋转矩阵之间的串联同样是正交的
7:复合变换
我们可以吧平移,旋转,缩放组合起来,来形成一个复杂的变换的过程,例如,可以对一个模型先进行大小为(2,2,2)的缩放,再绕y轴旋转30度,最后向z轴平移4个单位,符合变换可以通过矩阵的串联来实现,上面的变换过程可以使用下面的公式来计算
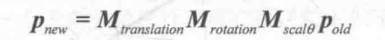
由于我们使用的是列矩阵,因此阅读顺序是从右到左,即先进性缩放变换,再进行旋转变换,最后进行平移变换,需要注意的是,变换的结果是依赖于变换顺序的,由于矩阵乘法不满足交换律,因此矩阵的乘法顺序很重要,也就是说,不同的变换顺序得到的结果可能是一样的,想象一下,如果让读者向前一步然后左转,记住此时的位置,然后回到原位,这次先左转再向前走一步,得到的位置和上一次是不一样的,究其本质,是因为矩阵的乘法不满足交换律,因此不同的乘法顺序得到的结果是不一样的
在绝大多数情况下,我们约定变换的顺序就是先缩放,再旋转,最后平移
为什么规定这样的变换顺序?
答:因为这样的变换顺序是我们需要的,想象我们对奶牛妞妞进行一个复合变换,如果我们按先平移,再缩放的顺序进行变换,假设初始情况下妞妞位于原点,我们先按(0,0,5)平移它,现在它距离原点5个单位,然后再将它放大2倍,这样所有的坐标都变成了原来的2倍,而这意味着妞妞现在的位置是(0,0,10),这不是我们希望的,正确的做法是,先缩放再平移,也就是说,我们先在原点对妞妞进行两倍的缩放,再进行平移,这样妞妞的大小正确了,位置也正确了,从数学公式上来看

这两者得到的变换矩阵也是不一样的
除了需要注意不同类型的变换顺序之外,我们有时还需要小心旋转的变换顺序,在上一个知识点中,我们分别给出了绕x,y,z轴的旋转变换矩阵,一个问题是,如果我们需要同时绕着3个轴进行旋转,是先绕x轴,再绕y轴,再绕z轴旋转,还是按照其他的旋转顺序呢?
当我们直接给出(θx,θy,θz)这样的旋转角度时,需要定义一个旋转顺序,在Unity中,这个旋转顺序是zxy,这在旋转相关的API文档里都有说明,这意味着,当给定(θx,θy,θz)这样的旋转角度时,得到的组合宣祖涵变换矩阵是:
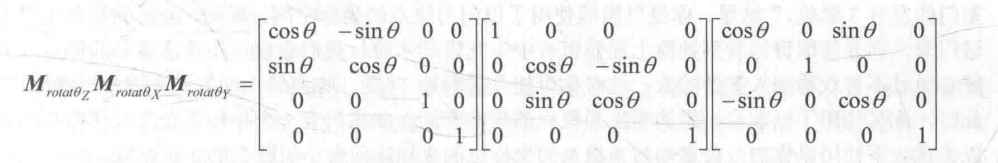
这里,一些读者可能会有疑问:上面的公式书写顺序是不是反了?不是说列矩阵要从右往左读吗?这样一来顺序不就颠倒了吗?实际上,有一个非常重要的东西还没有说清楚,那就是旋转时使用的坐标系,给定一个旋转顺序(例如这里的ZXY),以及它们对应的旋转角度(θx,θy,θz),有两种坐标系可以选择
@1:绕坐标系E下的z轴旋转θz,绕坐标系E下的y轴旋转θy,绕坐标系E下的x轴旋转θx,即进行一次旋转时不一起旋转当前坐标系
@2:绕坐标系E下的z轴旋转θz,在坐标系E下再绕z轴旋转θz后的新坐标系E’下的y轴旋转θy,在坐标系E‘下再绕y轴旋转θy后的新坐标E“下的x轴旋转θx,即在旋转时,把坐标系一起转动
很容易得出结论:这两种选择的结果是不一样的,但如果把它们的旋转顺序颠倒一下,它们得到的结果就会是一样的!说的明白点,在第一种情况下,按zxy顺序旋转和在第二种情况下,按yxz顺序旋转是一样的,而在Unity文档中,说明的旋转顺序指的是在第一种情况下的顺序



 浙公网安备 33010602011771号
浙公网安备 33010602011771号