Shader学习04【矩阵】
前言：矩阵在三维数学中的扮演了举足轻重的角色，在三维数学中，我们通常会使用矩阵来进行变换，一个矩阵可以把一个矢量从一个坐标空间转换到另一个坐标空间，例如，在顶点着色器中我们需要把顶点坐标从模型空间变换到齐次裁剪坐标系中，下面，我们就先来认识一下矩阵的概念
1：矩阵概念 矩阵长下面这副摸样
它是由M*N个标量构成的长方形数组，在上面的式子中，我们使用方括号来围住矩阵中的数字，而一些其他的资料可能会使用圆括号或花括号来表示，这都是等价的
既然网格结构，就意味着矩阵拥有行（row）列（column）之分。例如上面的例子就是一个3*4的矩阵，它有三行四列，据此，我们可以给出矩阵的一般表达式，以3*3的矩阵为例，它可以写成：
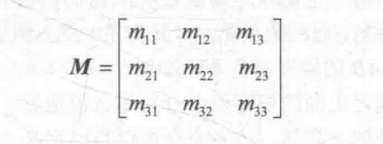
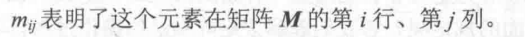
2：将矩阵和矢量联系起来
前面有说，矢量其实就是一个数组，而矩阵也是一个数组，既然都是数组，那就可以使用相同的方式进行思考，很容易就可以想到，我们可以用矩阵表示矢量，实际上，矢量可以看成是n*1的列矩阵（column matrix）或1*n的行矩阵，其中n对应了矢量的维度，例如矢量V（3，8，6）可以写成行矩阵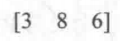
或者列矩阵
，那么为什么要将矢量和矩阵联系到一起呢，这是为了可以让矢量像一个矩阵一样一起参与矩阵运算，这在空间变换中将非常有用
到现在，使用行矩阵或者是列矩阵来表示矢量看起来是没什么分别的，的确，我们可以根据自己的喜好，来选择表示方法，但是，如果要和矩阵一起参与乘法运算时，这种选择会影响我们的书写顺序和结果。
3：矩阵运算
@1：矩阵与标量的乘法，规则就是，它们之间的乘法非常简单，就是矩阵的每一个元素和该标量相乘，以3*3的矩阵为例，公式如下：
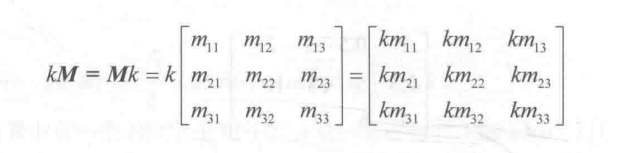
@2：矩阵和矩阵的乘法，一个r*n的矩阵A和一个n*c的矩阵B相乘，他们的结果AB将会是一个r*c大小的矩阵，观察他们的行列关系发现，第一个矩阵的列数必须和第二个矩阵的行数相同，它们相乘得到的矩阵的行数是第一个矩阵的行数，而列数是第二个矩阵的列数
那么如果两个矩阵的行列不满足上面的规定该怎么办呢，那么非常抱歉，这两个矩阵并不能相乘，因为他们之间的乘法是没有被定义的，至于为什么会有上面的规定，理解了矩阵乘法的操作过程自然就会明白
先给出看起来很复杂的数学表达式：
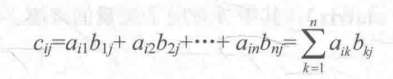
这个表达式看起来相当复杂，但是，我们可以用一个更简单的方式来解释：对于每一个元素C ij，我们找到A中的第i行和第j列，然后把他们对应元素相乘后再加起来，这个和就是Cij，因此，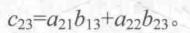
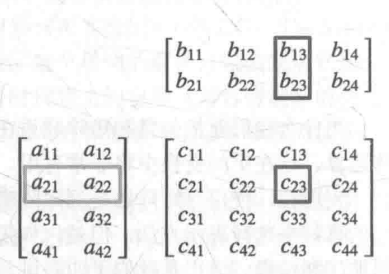
在Shader计算中，我们更多的是使用4*4的矩阵来运算的
矩阵乘法满足一些性质。
性质一：矩阵乘法并不满足交换律，通常情况下：AB≠BA
性质二：矩阵乘法满足结合律
也就是说
(AB)C=A(BC)
同理，矩阵乘法的结合律可以扩展到更多的矩阵相乘
4：特殊矩阵
有些特殊的矩阵类型在Shader中经常见到，这些特殊矩阵往往具有一些重要的性质
@1：方块矩阵(Square matrix)，简称方阵，是指那些行和列数目相等的矩阵，在三维渲染里，最常使用的就是3*3和4*4方阵
方阵之所以单独提出来，是因为矩阵的一些运算和性质是只有方阵才具有的，例如，对角元素（diagonal elements ）。方阵的对角元素指的是行号和列号相等的元素，例如m11,m12,m13等，如果把方阵看成一个正方形的话，这些元素排列在正方形的对角线上，这也是它们名字的由来，如果一个矩阵除了对角元素外所有的元素都为零，那么这个矩阵就叫做对角矩阵（diagonal matrix），下面就是一个4*4的对角矩阵
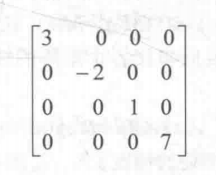
@2：单位矩阵
一个特殊的对角矩阵是单位矩阵（identity matrix），用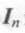
来表示，一个3*3的单位矩阵如下：
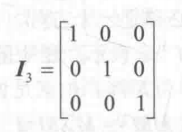
为什么要为这种矩阵单独起一个名字，这是因为，任何矩阵和它相乘的结果还是原来的矩阵，也就是说：MI=IM=M，宛如标量中的数字1
@3：转置矩阵
转置矩阵（transposed matrix）这种矩阵实际上是对原矩阵的一种运算，即转置运算，给定一个r*c的矩阵M，它的转置可以表示成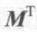
,这是一个c*r的矩阵，转置矩阵的计算非常简单，我们只需要把原来矩阵反转一下即可，也就是说，原矩阵的第i行变成了第i列，而第j列变成了第j行，数学公式是：
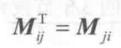，例如：
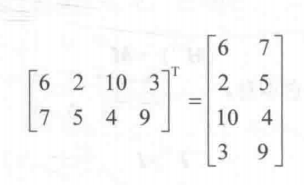
性质1：矩阵转置的转置等于原矩阵：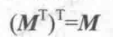
性质2：矩阵串接的转置，等于反向串接各个矩阵的转置，用公式表示就是：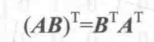
@4：逆矩阵
逆矩阵（inverse matrix）大概是本书讲到的关于矩阵最复杂的一种操作了，不是所有矩阵都有逆矩阵，第一个前提就是，该矩阵必须是一个方阵。
给定一个方阵M，它的逆矩阵用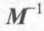
表示，逆矩阵的最重要的性质就是，如果我们把M和
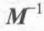相乘，那么他们的结果将会是一个单位矩阵，也就是说
前面说了，并非所有的方阵都有对应的逆矩阵，一个明显的例子就是一个所有元素都为0的矩阵，很显然，任何矩阵和它相乘都会得到一个零矩阵，即所有的元素仍然都是零，如果一个矩阵有对应的逆矩阵，我们就说这个矩阵是可逆的（invertible）或者说是非奇异的（noninvertible）或者说是奇异的（singular），逆矩阵有着如下性质：
性质一：逆矩阵的逆矩阵是原矩阵本身
假设矩阵M是可逆的，那么（M-1）-1=M
性质二：单位矩阵的逆矩阵是它本身
即I-1=I
性质三：转置矩阵的逆矩阵是逆矩阵的转置
即 (MT)-1=(M-1)T
性质四：矩阵串接相乘狗的逆矩阵等于反向串接各个矩阵的逆矩阵。
即(AB)-1=B-1A-1
这个性质可以扩展到更多矩阵的连乘，如(ABCD)-1=D-1C-1B-1A-1
逆矩阵具有几何意义的，我们知道一个矩阵可以表示一个变换，而逆矩阵允许我们还原这个变换，或者说是计算这个变换的反向变换，因此，我们使用变换矩阵M对矢量V进行了一次变换。然后再使用它的逆矩阵M-1进行另一次变换，那么我们就会得到原来的矢量
@5：正交矩阵
另一个特殊的方阵是正交矩阵（orthogonal matrix）。正交是矩阵的一种属性，如果一个方阵M和它的转置矩阵的乘积是单位矩阵的话，我们就说这个矩阵是正交的（orthogonal）。反过来也是成立的。也就是说，矩阵M是正交的等价于：
MMT=MTM=I
读者可能已经看出来，上式和所说的逆矩阵时遇到的公式很像，由此可以得到一个很重要的性质，即如果一个矩阵是正交的，那么它的转置矩阵和逆矩阵是一样的，也就是说，矩阵M是正交的等价于：MT=M-1
这个公式非常有用，因为在三维变换中我们经常会需要使用逆矩阵求解反向的变换，而逆矩阵的求解往往计算量很大，但转置矩阵却非常容易求解：我们只需要把矩阵翻转一下就可以了。那么，我们如何提前判断一个矩阵是否是正交矩阵呢？你们可能会想，判断MMT=I是否成立就可以了，但是求解这样的一个表达式无疑是需要一定的计算量的，这些计算量可能和直接求解逆矩阵无异。而且，如果我们判断出来这不是一正交矩阵，那么这些花在验证是否是正交矩阵上的计算就浪费了。因此，我们更想不需要计算，而仅仅根据一个矩阵的构造过程来判断这个矩阵是否是正交矩阵，为此，我们需要来了解正交矩阵的几何意义
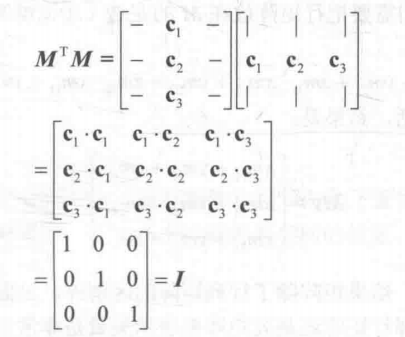
我们可以得出以下结论：矩阵的每一行，即C1，C2，C3是单位矢量，因为只有这样它们与自己的点积才能是1；
矩阵的每一行，即C1，C2，C3之间互相垂直，因为只有这样他们之间的点积才能是0.
上述两条结论对矩阵的每一列满足上面的条件，那么它就是一个正交矩阵，读者可以注意到，一组标准正交基可以精确的满足上述条件，在后续随笔中，我们使用坐标空间的基矢量来构建用于空间变换的矩阵，因此，如果这些基矢量是一组标准正交基的话（例如只存在旋转变换），那么我们就可以直接使用转置矩阵来求得该变换的逆变换。
这里区分一下标准正交，正交的概念：
我们应该知道，一个坐标空间需要指定一组基矢量，也就是我们理解的坐标轴，如果这些基矢量之间是互相垂直的，那么我们就把它们称为是一组正交基（orthogonal basis），但是他们的长度并不要求一定是1，如果他们的长度的确是1的话，那么，我们就成它们是一组标准正交基（orthonarmal basis）.因此，一个正交矩阵的行和列之间分别构成了一组标准正交基。但是，如果我们使用一组正交基来构建一个矩阵的话，这个矩阵可能就不是一个正交矩阵，因为这些基矢量的长度可能不为1。
5：行矩阵还是列矩阵
在学习矩阵的几何意义之前，我们有必要说明一下行矩阵和列矩阵的问题
前面说过，可以把一个矢量转换成一个行矩阵或者是列矩阵，他们本身是没有区别的，但是，当我们需要把它和另一个矩阵相乘时，就会出现一些差异
假设有一个矢量v=(x,y,z)，我们可以把它转换成行矩阵v=(x y z)或者是列矩阵v=(x y z)T,现在，有另一个矩阵M：
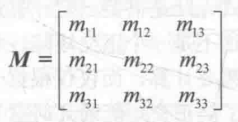
那么M分别和行矩阵以及列矩阵相乘后会是什么结果呢？我们先来看M和行矩阵的相乘，由矩阵乘法的定义可知，我们需要把行矩阵放在M的左边，即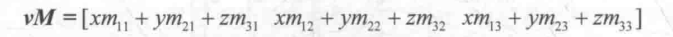
，如果和列矩阵相乘的话，结果是：
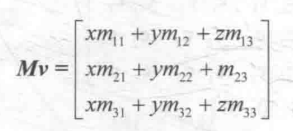，对比一下就会发现，结果矩阵除了行列矩阵的区别外，里面的元素也是不一样的，这就意味着，在和矩阵相乘时选择行矩阵还是列矩阵来表示矢量是非常重要的，因为这决定了矩阵乘法的书写次序和结果值。在Unity中，常规做法是把矢量放在矩阵的右侧，即把矢量转换成列矩阵来运算，因此，在后续进行矩阵变换时，如无特殊情况，我们都将使用列矩阵，这意味着，我们的矩阵乘法通常都是右乘，例如：
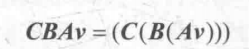
使用列向量的结果是，我们的阅读顺序是从右到左，即先对v使用A进行变换，再使用B进行变换，最后使用C进行变换，上面的计算等价于下面的行矩阵运算：
vATBTCT=(((vAT)BT)CT)
