随机过程中的 Inspection Paradox

笔者在做随机过程作业的时候遇见了一道题泊松过程的题目，凭借直觉填写答案后总觉得逻辑上理不太顺。但是一直也没想具体的原因（实在是懒啊~摸鱼不好吗），

今天上团课时候突然想起来，这里记录一下。

题目为如下的37题（来自龚光鲁11版习题），还算清晰，不再抄题了。

 

 这里求解的是两次替换之间的平均时间 = E(检修队连续两次发现故障并替换期间的时间)，此处的E表示均值的求解。

 

 解析图的符号：三角标志检修队到来检查，下标1,2，.....,i,i+1为次数

　　　　　　　x表示在此处器件已坏，√表示器件正常，或者检修队对坏的器件进行了更换。

这里需要注意的是，在“1”处之前器件已经损坏，当检修队以泊松在‘1’点到来，对其进行了第一次的更换。

在检修队第‘i’次抵达时器件仍然正常，从此处到第‘i+1’次检修队到达之间的时间，器件损坏。检修队第‘i+1’次抵达时候进行第二次的更换。

所以可以推导得：

　　　　两次器件更换的时间间隔 T = T1+T2。T1为从第一次更换后到器件再次毁坏的时间间隔，而T2是从毁坏到再次被检修队发现并且更换的时间间隔。

那么求平均即是 E(T) = E(T1+T2) = E(T1)+E(T2) , 这里的T1是只与器件的寿命有关的，完全服从参数为1/u的指数分布，故可求得第一部分的参数结果。

而在求解第二个分量 E(T2）的时候最开始的时候思路是混乱的，单纯凭借检修队行为是一种泊松过程，邻近两次的到达时间的间隔是服从参数为（后面用y表示）

的指数分布，即Si+1 - Si是服从 E(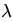）的。但是这里的T2 是Si+1 - Si的一部分，是否符合指数分布呢？如果符合，那就是说指数分布其部分分量也服从了相同参量的

指数分布，那我这里借助于对称性完全可以猜测Si+1 - Si中除了T2的另一部分T3 = {机器坏的时间 - 检修队第i次检修的时间}也服从相同参量的指数分布，那么有

Si+1 - Si = T2+T3，而三者都服从了指数分布，我们知道这是不可能的。（详情参考伽马分布与指数分布）

至此以上的假设必然有一种是错的：（1）泊松过程两个到达时间的间隔服从指数分布（T or F?）

　　　　　　　　　　　　　　　　   (2)  T2服从指数分布（T or F?）

我们知道（1）是以定理形式经过严格的数学推导给出的，不可能错（真的是这样吗？？QAQ~）,那么（2）必然就是错的，但是答案就是1/u+1/,按照这个答案来说

 

那（2）一定是正确的。本着有答案就算对，然后用答案倒推过程的精神，我在这里展开了探索发现这其实是泊松过程中的很经典的inspection 悖论。

 

先说结论：上面的（1）中的结论的确是对的，但是有条件：那就是必须得是两个确定的相邻的两个到达事件之间的间隔时间，而本题中的检修队到达次数 ‘ i ’也是

一个变量，在这种情况下（1）就不能用在本题的题设条件下。结果就是在本题中（1）不可用，（2）是符合的。

本文旨在用题目的解答过程来引出Inspection Paradox的结论，以使读者能够应用，具体的关于T2符合指数分布详细的数学推导和Inspection Paradox相关论证可参考文献。

故本题中T1~E( u ) ， T2~E（），最后结果：E(T) = E(T1+T2) = E(T1)+E(T2) = 1/u+1/