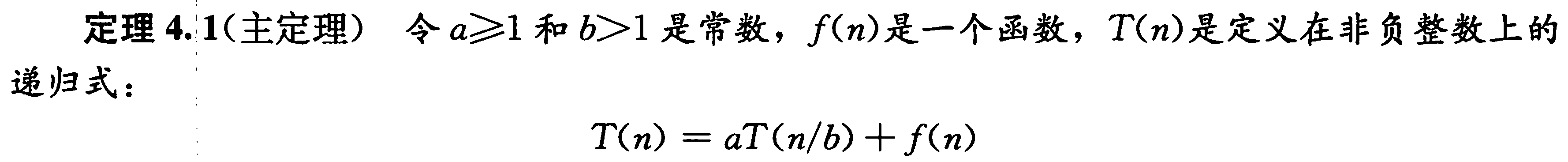算法导论笔记——第四章 分治策略

第四章 分治策略

　　分解，解决，合并

　　时间复杂度，求解递归式：代入法，递归树法，主方法

　　忽略细节：是否为整数，边界条件

4.1 最大数组问题

股票最大收益问题（LC有类似题目,存在线性算法：如果当前和大于0，与下一个累加。如果小于0，舍弃，从下一个重现开始求和。）

　　每日股票价格变为每日股票变化量，再计算最大子数组

　　可采用分治法，将其分为相等子数组，然后分别求最大子数组位于左边，右边，或者跨越中点，取最大值即可

　　T(n)=2T(n/2)+O(n)

4.2 代入法求解递归式

　　猜测，再递归证明

4.3 递归树法求解递归式

　　画出递归树

4.4 主方法求解递归式

　　T(n)=aT(n/b)+f(n)　　a>=1,b>1,f(n)为渐进正函数

　　它表示将规模为n的问题分解为a个子问题，每个子问题规模为n/b。

　　主定理：