bc38 1002, bc39 1002
比赛的时候是对于每个数，记录下来a[i]， 并记录该树的下标hash[a[i]]
然后枚举a[i]的倍数，如果a[i]的倍数存在(设为k*a[i])，那么vis[k*a[i]]是不为0的
那么可以这样枚举得到最小的下标，但是比赛的时候不懂算时间复杂度，就随便提交了一下，没想到过了。
后来看了下题解，原来时间复杂度是这样算的
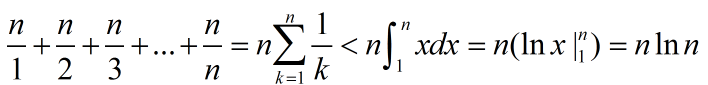
1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef long long LL; 16 const int INF = 1<<30; 17 /* 18 19 */ 20 const int N = 10000 + 10; 21 int vis[N]; 22 int a[N]; 23 int main() 24 { 25 int n, i, ans,j; 26 while (scanf("%d", &n) != EOF) 27 { 28 memset(vis, 0, sizeof(vis)); 29 for (i = 1; i <= n; ++i) 30 { 31 scanf("%d", &a[i]); 32 vis[a[i]] = i; 33 } 34 ans = 0; 35 for (i = 1; i <= n; ++i) 36 { 37 bool find = false; 38 int index; 39 for (j = 2; j*a[i] <= 10000; ++j) 40 { 41 int v = j * a[i]; 42 //找到最小的下标 43 if (!vis[v]) 44 continue; 45 if (vis[v] < i) 46 continue; 47 if (!find) 48 { 49 index = vis[v]; 50 find = true; 51 } 52 else 53 index = min(index, vis[v]); 54 55 } 56 if (find) 57 ans += index; 58 } 59 printf("%d\n", ans); 60 } 61 return 0; 62 }
然后想起bc38场的第2题好像也是类似这样子。
我可以hash每个数，即hash[a[i]]++
然后从大到小枚举约数，然后再枚举约数的倍数，如果出现过两次约数的倍数，那么该约数就是最大的约数。 需要注意的是因为a[i]可能重复，所以hash[a[i]]++
这题的时间复杂度和上面一样，也是O(nlgn)
1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef long long LL; 16 const int INF = 1<<30; 17 /* 18 19 */ 20 const int N = 100000 + 10; 21 int a[N]; 22 int vis[N]; 23 int main() 24 { 25 int t, n, i, k; 26 int ans,Max; 27 scanf("%d", &t); 28 for (k = 1; k <= t; ++k) 29 { 30 Max = -1; 31 scanf("%d", &n); 32 memset(vis, 0, sizeof(vis)); 33 for (i = 0; i < n; ++i) 34 { 35 scanf("%d", &a[i]); 36 Max = max(Max, a[i]); 37 vis[a[i]] ++; 38 } 39 for (i = Max; i >= 1; --i)//枚举约数 40 { 41 int flag = 0; 42 for (int j = 1; j*i <= Max; ++j)//枚举约数的倍数， 43 { 44 int v = j * i; 45 flag += vis[v]; 46 if (flag >=2) 47 break; 48 } 49 if (flag >= 2) 50 break; 51 } 52 printf("Case #%d: %d\n", k, i); 53 } 54 return 0; 55 }
