求有重边的无向图的割边算法
如果图没有重边，那么一般的求割边tarjan算法是这么操作的。
dfs访问每一个点时，为这个点分配一个时间戳dfn[]，根据访问次序的先后，时间戳从小到大
对于边(u,v)是不是割边，如果lowv > dfn[u],那么边(u,v)是割边，反之不是。 lowv表示的是从点v开始dfs，所能访问到的最小时间戳。
如果从点v开始dfs，访问到的时间戳<=dfn[u]那么说明v或者v的子树有一条连向u或者u祖先的边。
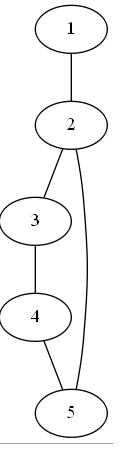
从点1开始dfs，dfn[1] = 1, 沿边访问到点2，然后从点2开始dfs，但是点2没有连回1的边，所以边(1,2)是割边
1 #include <stdio.h> 2 #include <string.h> 3 #include <vector> 4 using namespace std; 5 const int N = 1000 + 10; 6 vector<int> g[N]; 7 int dfs_clock,pre[N]; 8 int cnt; 9 int dfs(int u, int fa) 10 { 11 int lowu = pre[u] = ++dfs_clock; 12 int i,v,lowv; 13 for(i=0; i<g[u].size(); ++i) 14 { 15 v = g[u][i]; 16 if(!pre[v]) 17 { 18 lowv = dfs(v,u); 19 lowu = min(lowu,lowv); 20 if(lowv > pre[u])//相对于割点，只把等号给去掉了 21 cnt++; 22 } 23 else if(v!=fa && pre[v]<lowu)//v!=fa，说明不能用反向边来更新 24 lowu = pre[v]; 25 } 26 return lowu; 27 } 28 int main() 29 { 30 int i,x,y; 31 int n,m; 32 scanf("%d%d",&n,&m); 33 for(i=0; i<m; ++i) 34 { 35 scanf("%d%d",&x,&y); 36 g[x].push_back(y); 37 g[y].push_back(x); 38 } 39 dfs(1,-1); 40 41 printf("%d\n",cnt); 42 }
但是事实上，图经常有重边，而且题目经常喜欢重边，但是又不会给出说明，所以为了安全起见，要学会怎么处理有重边的无向图的割桥。
上面的tarjan算法有两个参数(u,fa),其中参数fa用来判断(x,t)是不是刚刚走过来的那条边，即如果fa==t，说明是刚刚走过来的那条边
在有重边的情况下， 这样就不太好判断了
如图
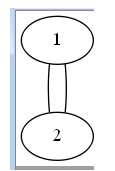因为是重边，所以边(1,2)不是割桥。，1走到2，我们可以从2走到1，但是如果按照上面的tarjan算法，由于是用点来判断某条边是不是走过
那么重边的情况下，就会误判。
为了防止误判，我们要用边来判断。
具体实现是我们给边编号，因为存边的时候，是分为两条有向边存储的，我们让编号从0开始，那么如果两条有向边的编号/2是相等的，那么就说明这两条边是一条边
而参数fa改成刚刚走过的边的编号
1从id为0的边走到2，不能从id为1的边走到1，但是可以从id为3的边走到1.
1 #include <stdio.h> 2 #include <string.h> 3 #include <vector> 4 using namespace std; 5 const int N = 5000; 6 struct node 7 { 8 int v,id; 9 }; 10 vector<node> g[N]; 11 int dfn[N],dfs_clock,cntCut; 12 int dfs(int u, int id) 13 { 14 int lowu = dfn[u] = ++dfs_clock; 15 int lowv,i,v; 16 for(i=0; i<g[u].size();++i) 17 { 18 v = g[u][i].v; 19 if(!dfn[v]) 20 { 21 lowv = dfs(v,g[u][i].id); 22 lowu = min(lowu,lowv); 23 if(lowv > dfn[u]) 24 cntCut++; 25 } 26 else if(id/2 != g[u][i].id/2 &&dfn[v]<lowu)//如果刚才走过来的边的id/2和这个边的id/2不相等，那么说明这两条有向边不是从一条边分离出来的 27 lowu = dfn[v]; 28 } 29 return lowu; 30 } 31 int main() 32 { 33 int n,m,i,a,b; 34 scanf("%d%d",&n,&m); 35 for(i=0; i<m; ++i) 36 { 37 scanf("%d%d",&a,&b); 38 node t; 39 t.v = a; 40 t.id = i * 2;//给边编号 41 g[b].push_back(t); 42 t.v = b; 43 t.id = i * 2 + 1; 44 g[a].push_back(t); 45 } 46 dfs(1,-2); 47 printf("%d\n",cntCut); 48 return 0; 49 }
其实还有更简单的办法，因为如果有重边(u,v), 那么边(u,v)肯定被存了两次，所以我们只要让它第二次访问时通过就可以了
1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 typedef long long LL; 15 const int INF = 1<<30; 16 const int N = 1000 + 10; 17 int dfn[N],low[N],dfs_clock; 18 vector<int> g[N]; 19 int cntCut; 20 void tarjan(int u, int fa) 21 { 22 dfn[u] = low[u] = ++dfs_clock; 23 bool flag = false; 24 for(int i=0; i<g[u].size(); ++i) 25 { 26 int v = g[u][i]; 27 if(v==fa && !flag)//如果有重边，那么边(u,v)被存了两次，所以，如果第二次访问，就让他通过 28 { 29 flag = true; 30 continue; 31 } 32 if(dfn[v]==0) 33 tarjan(v,u); 34 low[u] = min(low[u],low[v]); 35 if(low[v] > dfn[u]) 36 cntCut++; 37 } 38 } 39 int main() 40 { 41 int n,m,i,a,b; 42 scanf("%d%d",&n,&m); 43 for(i=0; i<m; ++i) 44 { 45 scanf("%d%d",&a,&b); 46 g[a].push_back(b); 47 g[b].push_back(a); 48 } 49 tarjan(1,-1); 50 printf("%d\n",cntCut); 51 return 0; 52 }
