【大语言模型基础】图解GPT原理-60行numpy实现GPT
写在前面
本文主要是对博客 https://jaykmody.com/blog/gpt-from-scratch/ 的精简整理,并加入了自己的理解。
中文翻译:https://jiqihumanr.github.io/2023/04/13/gpt-from-scratch/#circle=on
项目地址:https://github.com/jaymody/picoGPT
本文将用60行代码实现一个GPT,它可以加载OpenAI预训练的GPT-2模型权重来成文本。 注:本文仅实现了GPT模型的推理(无batch,不能训练)
一、GPT简介
GPT(Generative Pre-trained Transformer)基于Transformer解码器自回归地预测下一个Token,从而进行了语言模型的建模。
只要能足够好地预测下一个Token,语言模型便可能有足够潜力实现真正的智能
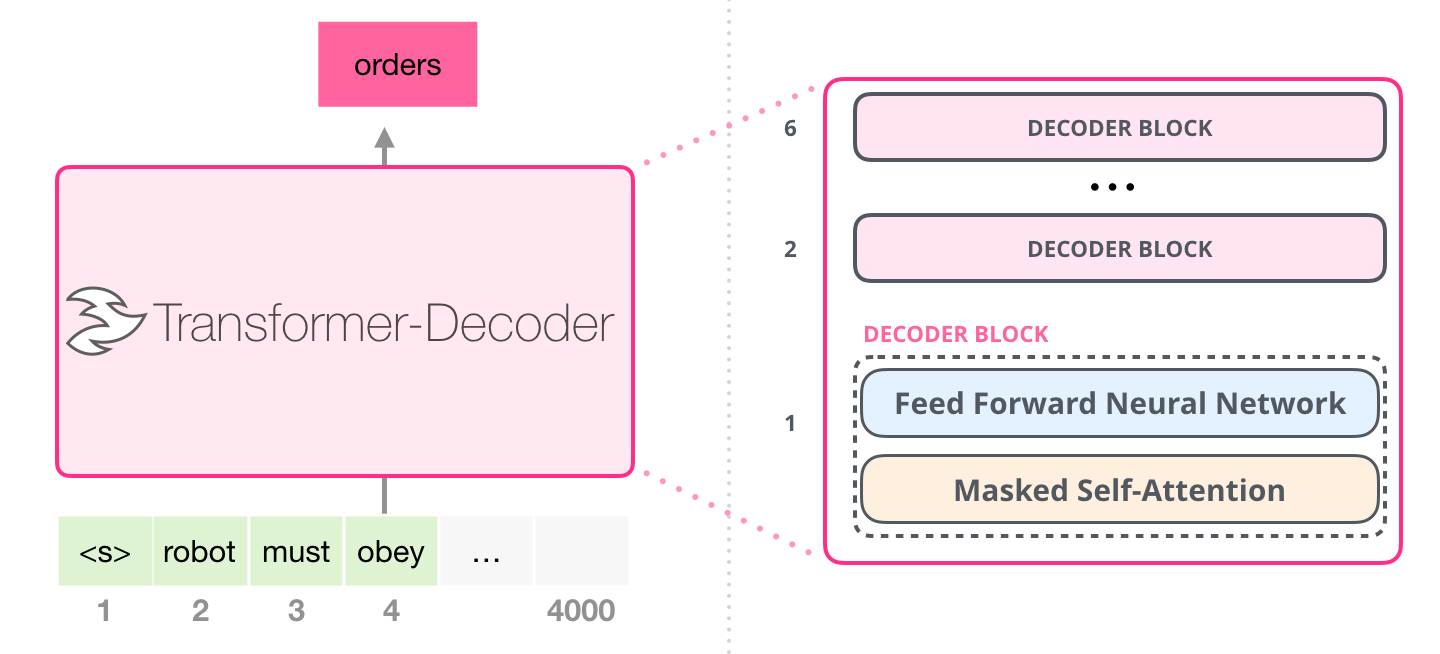
1.1 输入 / 输出
GPT的函数签名大致如下:
def gpt(inputs: list[int]) -> list[list[float]]:
""" GPT代码,实现预测下一个token
inputs:List[int], shape为[n_seq],输入文本序列的token id的列表
output:List[List[int]], shape为[n_seq, n_vocab],预测输出的logits列表
"""
output = # 需要实现的GPT内部计算逻辑
return output
输入
输入是一些由整数表示的文本序列,每个整数都与文本中的token对应。例如:
text = "robot must obey orders"
tokens = ["robot", "must", "obey", "orders"]
inputs = [1, 0, 2, 4]
token, 即词元,是文本的子片段,使用某种分词器生成。
分词器将文本分割为不可分割的词元单位,实现文本的高效表示,且方便模型学习文本的结构和语义。
分词器对应一个词汇表,我们可用词汇表将token映射为整数:
# 词汇表中的token索引表示该token的整数ID
# 例如,"robot"的整数ID为1,因为vocab[1] = "robot"
vocab = ["must", "robot", "obey", "the", "orders", "."]
# 一个根据空格进行分词的分词器tokenizer
tokenizer = WhitespaceTokenizer(vocab)
# encode()方法将str字符串转换为list[int]
ids = tokenizer.encode("robot must obey orders") # ids = [1, 0, 2, 4]
# 通过词汇表映射,可以看到实际的token是什么
tokens = [tokenizer.vocab[i] for i in ids] # tokens = ["robot", "must", "obey", "orders"]
# decode()方法将list[int] 转换回str
text = tokenizer.decode(ids) # text = "robot must obey orders"
简而言之:
- 通过语料数据集和分词器tokenizer可以构造一个包含文本中的所有token的词汇表vocab。
- 使用tokenizer将文本text分割为token序列,再使用词汇表vocab将token映射为token id整数,从而得到输入文本token序列。
最后,可以通过vocab将token id序列再转换回文本。
输出
output是一个二维数组,其中output[i][j]表示文本序列的第i个位置的token(inputs[i])是词汇表的第j个token(vocab[j])的概率(实际为未归一化的logits得分)。例如:
inputs = [1, 0, 2, 4] # "robot" "must" "obey" "orders"
vocab = ["must", "robot", "obey", "the", "orders", "."]
output = gpt(inputs)
# output[0] = [0.75, 0.1, 0.15, 0.0, 0.0, 0.0]
# 给定 "robot",模型预测 "must" 的概率最高
# output[1] = [0.0, 0.0, 0.8, 0.1, 0.0, 0.1]
# 给定序列 ["robot", "must"],模型预测 "obey" 的概率最高
# output[-1] = [0.0, 0.0, 0.1, 0.0, 0.85, 0.05]
# 给定整个序列["robot", "must", "obey"],模型预测 "orders" 的概率最高
next_token_id = np.argmax(output[-1]) # next_token_id = 4
next_token = vocab[next_token_id] # next_token = "orders"
在上述例子中,输入序列为["robot", "must", "obey"],GPT模型根据输入,预测序列的下一个token是"orderst",因为 output[-1][4]的值为0.85,是词表中最高的一个。
- output[0] 表示给定输入token "robot",模型预测下一个token可能性最高的是"must",为0.75。
- output[-1] 表示给定整个输入序列 ["robot", "must", "obey"],模型预测下一个token是"orders"的可能性最高,为0.85。
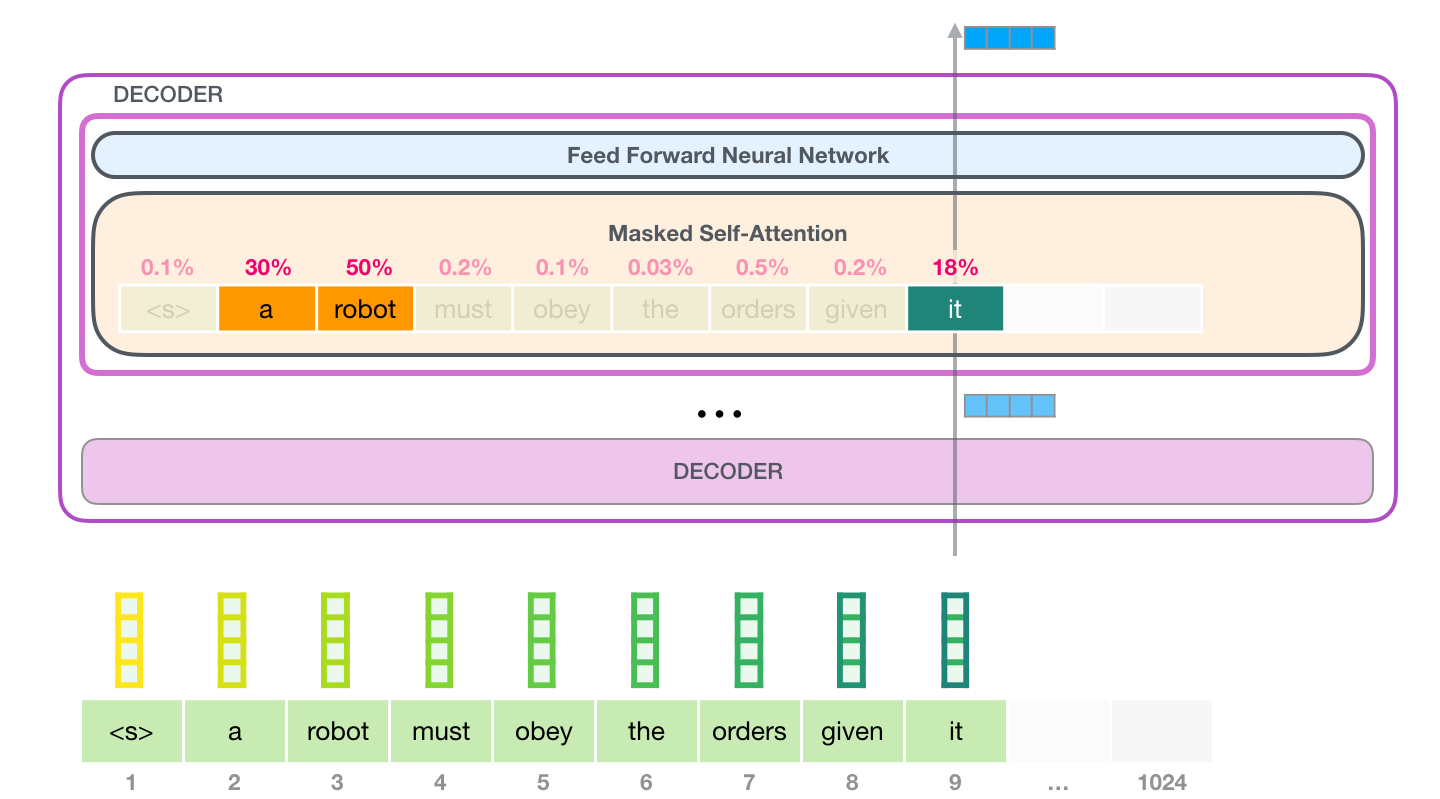
为预测序列的下一个token,只需在output的最后一个位置中选择可能性最高的token。那么,通过迭代地将上一轮的输出拼接到输入,并送入模型,从而持续地生成token。
这种生成方式称为贪心采样。实际可以对类别分布用温度系数T进行蒸馏(放大或减小分布的不确定性),并截断类别分布的按top-k,再进行类别分布采样。
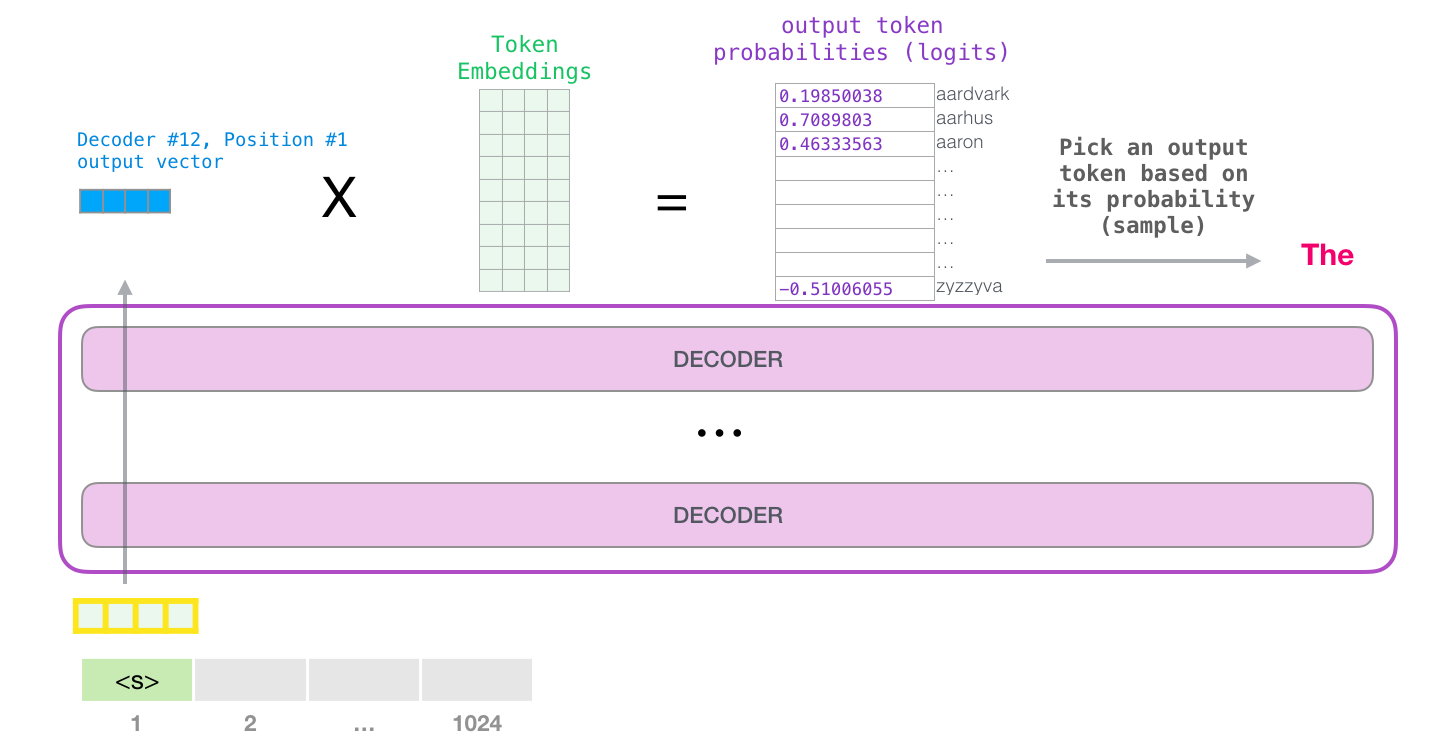
具体地,在每次迭代中,将上一轮预测出的token添加到输入末尾,然后预测下一个位置的值,如此往复,就是整个自回归的预测过程:
def generate(inputs, n_tokens_to_generate):
""" GPT生成代码
inputs: list[int], 输入文本的token ids列表
n_tokens_to_generate:int, 需要生成的token数量
"""
# 自回归式解码循环
for _ in range(n_tokens_to_generate):
output = gpt(inputs) # 模型前向推理,输出预测词表大小的logits列表
next_id = np.argmax(output[-1]) # 贪心采样
inputs.append(int(next_id)) # 将预测添加回输入
return inputs[len(inputs) - n_tokens_to_generate :] # 只返回生成的ids
# 随便举例
input_ids = [1, 0, 2] # ["robot", "must", "obey"]
output_ids = generate(input_ids, 1) # output_ids = [1, 0, 2, 4]
output_tokens = [vocab[i] for i in output_ids] # ["robot", "must", "obey", "orders"]
二、GPT结构与实现
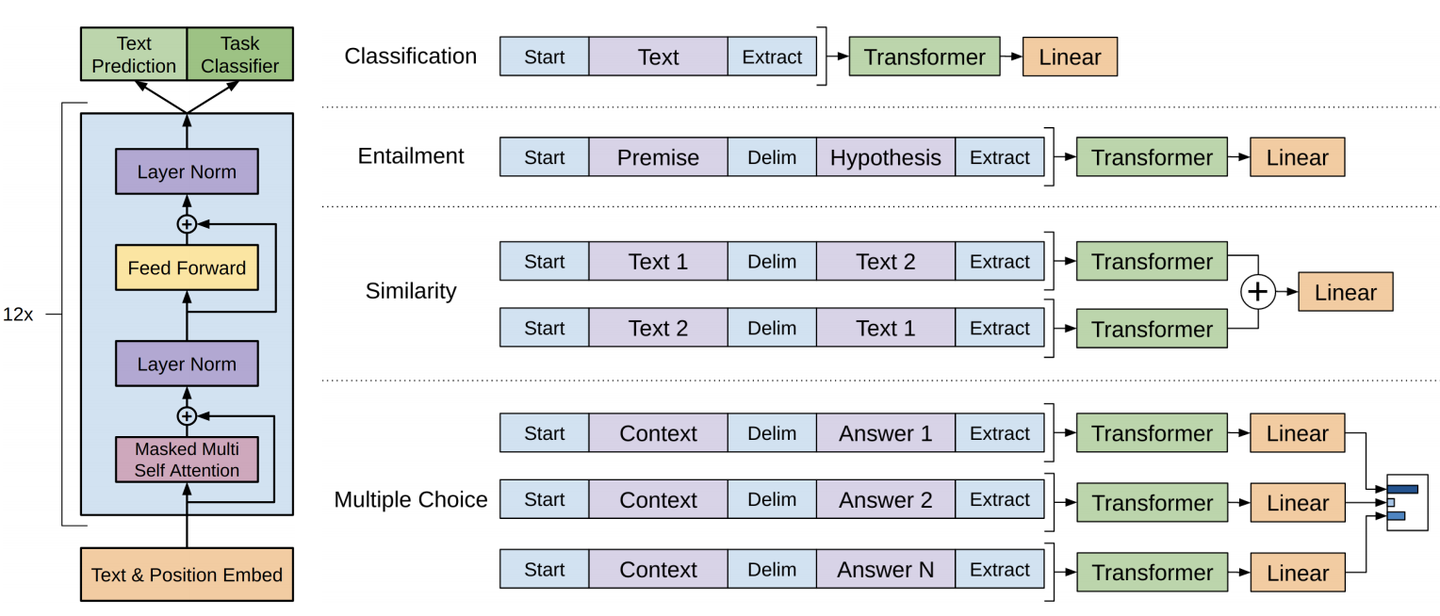
2.1 基本组成部分
首先,导入相关可视化函数
import random
import numpy as np
import matplotlib.pyplot as plt
def plot(x, y, x_axis=None, y_axis=None):
plt.plot(x, y)
if x_axis and isinstance(x_axis, tuple):
plt.xlim(x_axis[0], x_axis[1])
if y_axis and isinstance(y_axis, tuple):
plt.ylim(y_axis[0], y_axis[1])
plt.show()
def plotHot(w):
plt.figure()
plt.imshow(w, cmap='hot', interpolation='nearest')
plt.show()
GELU
GPT-2的FFN中的非线性激活函数是GELU(高斯误差线性单元),是ReLU的一种替代方法。它由以下函数近似表示:
def gelu(x):
return 0.5 * x * (1 + np.tanh(np.sqrt(2 / np.pi) * (x + 0.044715 * x**3)))
def relu(x):
return np.maximum(0, x)
GELU与ReLU的对比
print(gelu(np.array([1, 2, -2, 0.5])))
print(relu(np.array([1, 2, -2, 0.5])))
x = np.linspace(-4, 4, 100)
plot(x, np.array([gelu(x), relu(x)]).transpose())
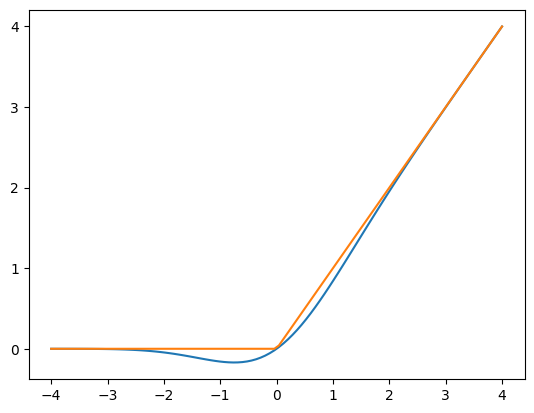
Softmax
原始Softmax公式:$$\text{softmax}(x)_i = \frac{e^{x_i}}{\sum_j e^{x_j}}$$
相比原始Softmax, 这里使用了减去最大值max(x)技巧来保持数值稳定性。
def softmax(x):
# 减去最大值,避免溢出,不影响分布
exp_x = np.exp(x - np.max(x, axis=-1, keepdims=True))
return exp_x / np.sum(exp_x, axis=-1, keepdims=True)
def rawSoftmax(x):
exp_x = np.exp(x)
return exp_x / np.sum(exp_x)
num = 100 # 生成不重复的随机数,比较 原始值、原始softmax和修正后的softmax
numbers = []
for i in range(num):
number = random.uniform(1, 3)
while number in numbers:
number = random.uniform(1, 3)
numbers.append(number)
plot(np.array(range(num)), np.array([numbers, rawSoftmax(numbers), softmax(numbers)]).transpose())
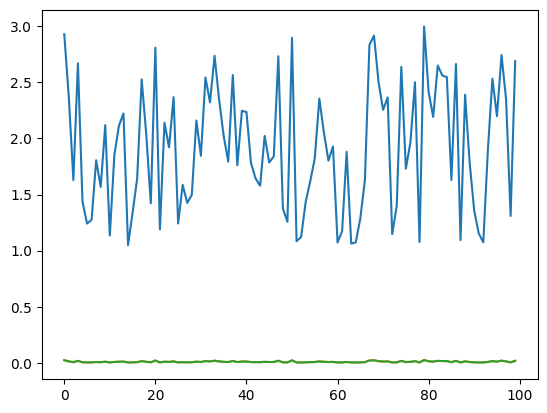
raw_x = np.array([[-200, 100, -300, 0, 70000000]])
x1 = softmax(raw_x)
x2 = rawSoftmax(np.array(raw_x))
print(x1, x1.sum(axis=-1), softmax(x1))
print(x2, x2.sum(axis=-1), softmax(x2))
在输入存在异常值时,输出结果比较(原始softmax出现nan)
[[0. 0. 0. 0. 1.]] [1.] [[0.14884758 0.14884758 0.14884758 0.14884758 0.40460968]]
[[ 0. 0. 0. 0. nan]] [nan] [[nan nan nan nan nan]]
tmp.py:7: RuntimeWarning: overflow encountered in exp exp_x = np.exp(x)
tmp.py:8: RuntimeWarning: invalid value encountered in divide return exp_x / np.sum(exp_x)
层归一化
层归一化(Layer Normalization)是基于特征维度将数据进行标准化(均值为0方差为1),同时乘以缩放系数、加上平移系数,保留其非线性能力:
层归一化可以有效地缓解优化过程中潜在的不稳定、收敛速度慢等问题。
def layer_norm(x, g, b, eps: float = 1e-5):
""" 层归一化操作
x: np.array, 输入
g: float, 可学习的缩放参数 gamma
b: float, 可学习的平移参数 beta
eps: float, 避免方差为0从而除零的极小值
"""
mean = np.mean(x, axis=-1, keepdims=True)
variance = np.var(x, axis=-1, keepdims=True)
x = (x - mean) / np.sqrt(variance + eps) # 将x沿着最后一个轴,进行标准化
return g * x + b # 将标准化后的x进行重新缩放和平移
可视化例子
num, dim = 5, 5
x = np.array([[random.randint(-10, 10) for _ in range(dim)] for _ in range(num)] )
g, b = 1, 0 # 不缩放和平移
x_norm = layer_norm(x, g, b)
print(x)
print(x_norm)
plotHot(x)
plotHot(x_norm)
输出结果
# 层归一化前
[[ -9 3 -2 -6 -6]
[-10 -6 -10 8 4]
[ -1 5 -4 -3 -5]
[ 8 7 -5 -5 9]
[ 10 -1 -5 3 9]]
# 层归一化后
[[-1.2056067 1.68784939 0.48224268 -0.48224268 -0.48224268]
[-0.96768591 -0.43008263 -0.96768591 1.45152886 0.91392558]
[ 0.16876312 1.8563943 -0.67505247 -0.39378061 -0.95632434]
[ 0.8124999 0.65624992 -1.21874985 -1.21874985 0.96874988]
[ 1.18444594 -0.73156955 -1.42830246 -0.03483665 1.01026272]]
层归一化前
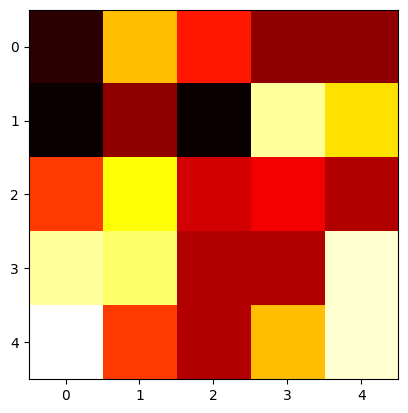
层归一化后(每行数据经过标准化后,分布差异变小了,从而输入网络的数据的分布得到了限制)
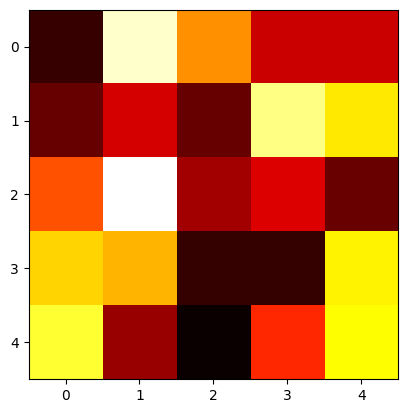
通过折线图可视化(每条折线代表一个行向量),可以更明显地看到变化:
axis = np.array(range(x.shape[0]))
plot(axis, x)
plot(axis, x_norm)
层归一化前
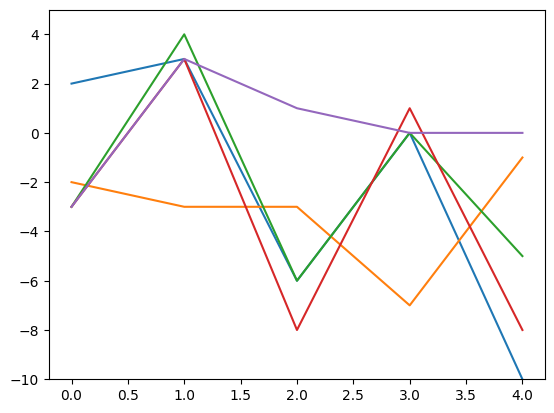
层归一化后
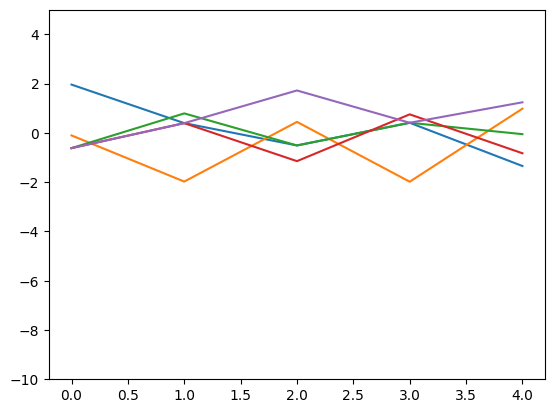
线性层(仿射变换)
标准的矩阵乘法+偏置:
def linear(x, w, b): # [m, in], [in, out], [out] -> [m, out]
return x @ w + b
例子
n_num = 3
in_dim, hid_dim = 4, 4
x = np.random.normal(size=(n_num, in_dim))
w = np.random.normal(size=(in_dim, hid_dim))
b = np.random.normal(size=(hid_dim,))
h = linear(x, w, b)
print(f"shape of w: {w.shape}")
print(f"input shape: {x.shape}, output shape: {h.shape}")
plotHot(w)
shape of w: (4, 4)
input shape: (3, 4), output shape: (3, 4)
权重可视化
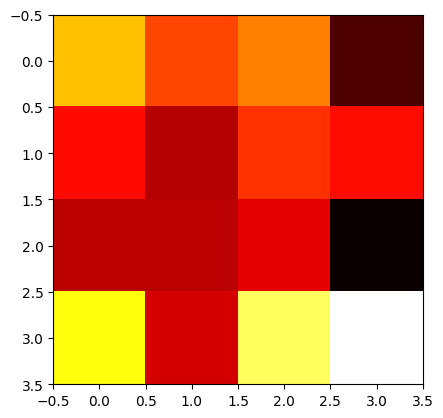
2.2 GPT架构
从整体上来看,GPT架构分为三个部分:
- 嵌入表示层:文本词元嵌入(token embeddings) + 位置嵌入(positional embeddings)
- transformer解码器堆栈:多个transformer decoder block堆叠
- 预测:输出投影回词汇表(projection to vocab)
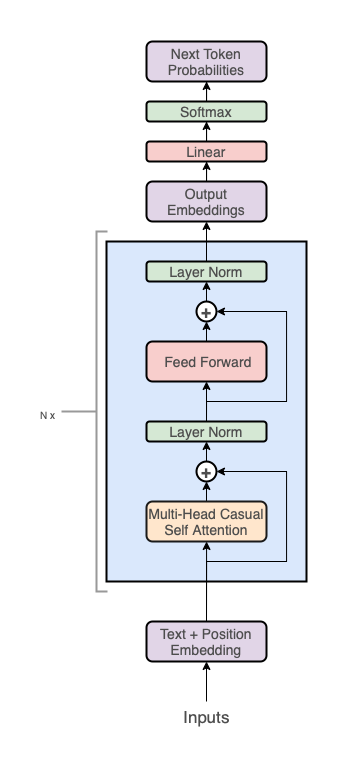
GPT实现
def gpt2(inputs, wte, wpe, blocks, ln_f, n_head):
""" GPT2模型实现
输入输出tensor形状: [n_seq] -> [n_seq, n_vocab]
n_vocab, 词表大小
n_seq, 输入token序列长度
n_layer, 自注意力编码器的层数
n_embd, 词表的词元嵌入大小
n_ctx, 输入最大序列长度(位置编码支持的长度,可用ROPE旋转位置编码提升外推长度)
params:
inputs: List[int], token ids, 输入token ids
wte: np.ndarray[n_vocab, n_embd], token嵌入矩阵 (与输出分类器共享参数)
wpe: np.ndarray[n_ctx, n_embd], 位置编码嵌入矩阵
blocks:object, n_layer层因果自注意力编码器
ln_f:tuple[float], 层归一化参数
n_head:int, 注意力头数
"""
# 1、在词元嵌入中添加位置编码信息:token + positional embeddings
x = wte[inputs] + wpe[range(len(inputs))] # [n_seq] -> [n_seq, n_embd]
# 2、前向传播n_layer层Transformer blocks
for block in blocks:
x = transformer_block(x, **block, n_head=n_head) # [n_seq, n_embd] -> [n_seq, n_embd]
# 3、Transformer编码器块的输出投影到词汇表概率分布上
# 预测下个词在词表上的概率分布[ 输出语言模型的建模的条件概率分布p(x_t|x_t-1 ... x_1) ]
x = layer_norm(x, **ln_f) # [n_seq, n_embd] -> [n_seq, n_embd]
# 就是和嵌入矩阵进行内积(编码器块的输出相当于预测值,内积相当于求相似度最大的词汇)
return x @ wte.T # [n_seq, n_embd] -> [n_seq, n_vocab]
当最后一个 transformer block产生输出之后(即经过了它自注意力层和神经网络层的处理),模型会将输出的向量乘上Token Embeddings矩阵
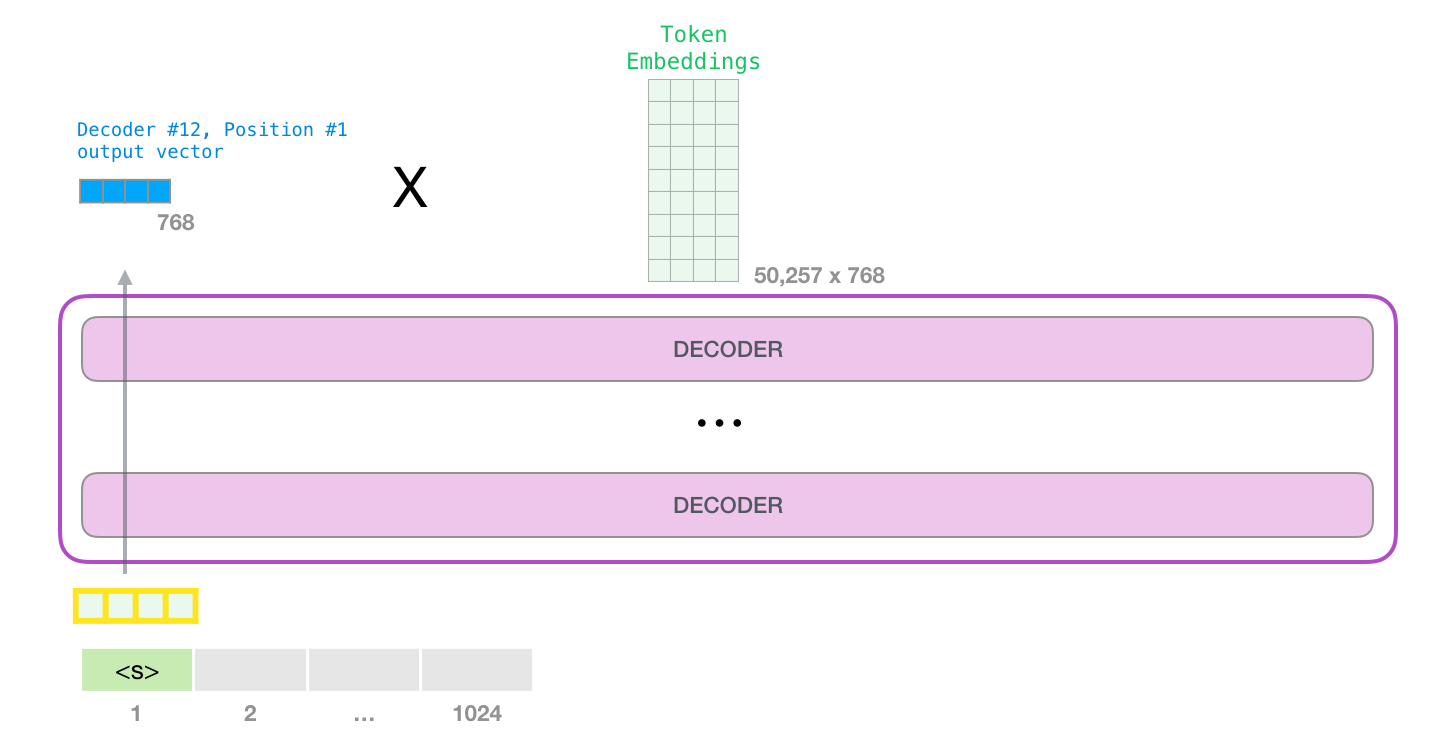
Token Embeddings矩阵的每一行都对应模型的词汇表中一个Token的嵌入向量。该乘法操作得到的结果就是预测的下一个Token和词汇表中每个Token的相似度得分(内积值,此处Token Embeddings矩阵可视为分类器的权重矩阵)。
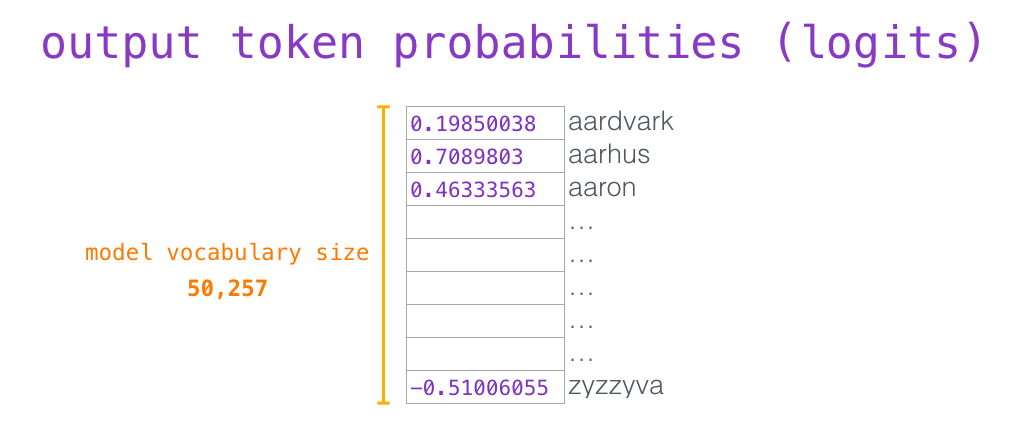
嵌入表示层
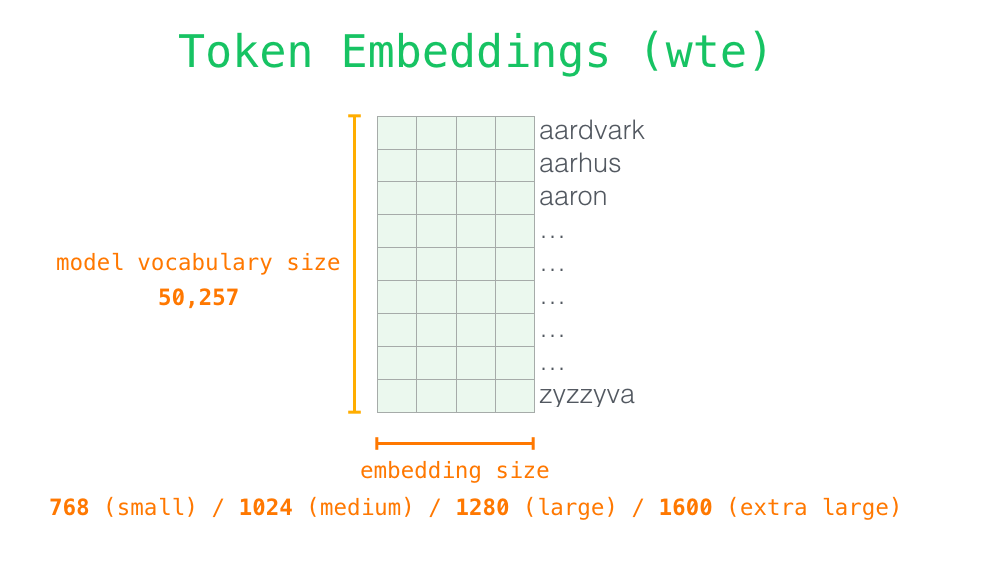
Token embeddings
wte是一个[n_vocab, n_embd]可学习参数矩阵,它充当一个token嵌入查找表,其中矩阵的第\(i\)行对应于我们词汇表中第 \(i\)个token的embedding。
Positional embeddings
为了编码序列的顺序信息,通过在输入表示中添加位置编码(positional encoding)嵌入来注入位置信息。
位置编码可以通过学习得到也可以直接固定得到。
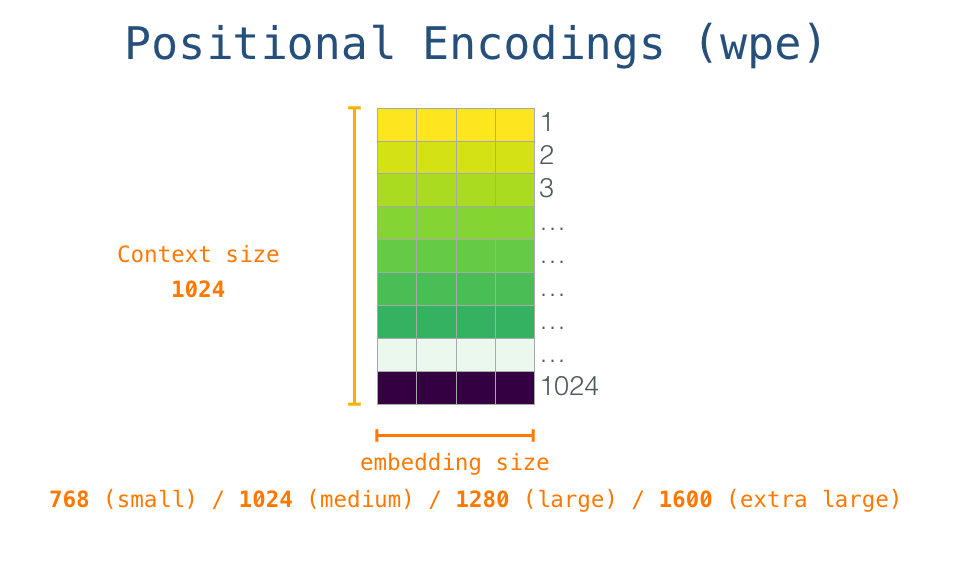
在GPT中,位置嵌入矩阵wpe和token embeddings类似,先随机初始化,后通过训练学习得到。wpe[inputs] 使用整数数组索引inputs来检索与输入中每个token对应的位置嵌入。
Token + Positional embeddings
将Token embeddings与位置嵌入拼接后的嵌入,将token信息和位置信息都编码进来了,它将作为transoformer decoder blocks的实际输入。
x = wte[inputs] + wpe[range(len(inputs))] # [n_seq] -> [n_seq, n_embd]

GPT解码层
GPT的解码层中,堆叠了\(n\)个如下的transformer_block解码器模块:
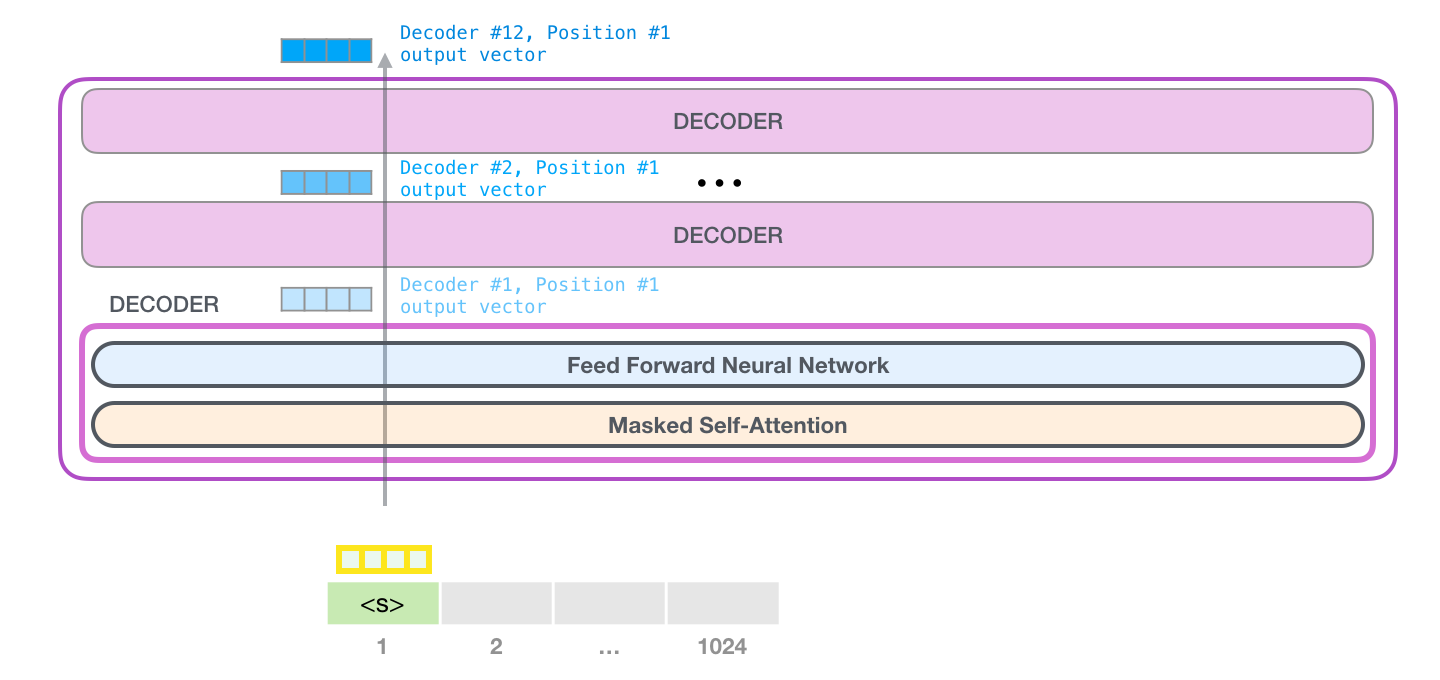
transformer_block解码器模块由两个子层组成:
- 多头因果自注意力(Multi-head causal self attention)
- 位置感知的前馈网络(Position-wise feed forward neural network)
解码器模块实现
def transformer_block(x, mlp, attn, ln_1, ln_2, n_head):
""" 解码器模块 (只实现逻辑,各个子模块参数需传入)
输入输出tensor形状: [n_seq, n_embd] -> [n_seq, n_embd]
n_seq, 输入token序列长度
n_embd, 词表的词元嵌入大小
params:
x: np.ndarray[n_seq, n_embd], 输入token嵌入序列
mlp: object, 前馈神经网络
attn: object, 注意力编码器层
ln1: object, 线性层1
ln2: object, 线性层2
n_head:int, 注意力头数
"""
# Multi-head Causal Self-Attention (层归一化 + 多头自注意力 + 残差连接 )
# Self-Attention中的层规一化和残差连接用于提升训练的稳定性
x = x + mha(layer_norm(x, **ln_1), **attn, n_head=n_head) # [n_seq, n_embd] -> [n_seq, n_embd]
# Position-wise Feed Forward Network
x = x + ffn(layer_norm(x, **ln_2), **mlp) # [n_seq, n_embd] -> [n_seq, n_embd]
return x
接下来,将先介绍 1)位置感知的前馈网络,再介绍 2)因果自注意力
残差连接
残差连接引入输入直接到输出的通路,便于梯度回传从而缓解在优化过程中由于网络过深引起的梯度消失问题。
位置感知的前馈网络
对序列中的所有位置的表示进行变换时使用的是同一个2层隐藏层的MLP,故称其为position-wise的前馈网络(Position-wise Feed Forward Network)。
def ffn(x, c_fc, c_proj):
""" 2层前馈神经网络实现 (只实现逻辑,各个子模块参数需传入)
输入输出tensor形状: [n_seq, n_embd] -> [n_seq, n_embd]
n_seq, 输入token序列长度
n_embd, 词表的词元嵌入大小
n_hid, 隐藏维度
params:
x: np.ndarray[n_seq, n_embd], 输入token嵌入序列
c_fc: np.ndarray[n_embd, n_hid], 升维投影层参数, 默认:4*n_embd
c_proj: np.ndarray[n_hid, n_embd], 降维投影层参数
"""
# project up:将n_embd投影到一个更高的维度 4*n_embd
a = gelu(linear(x, **c_fc)) # [n_seq, n_embd] -> [n_seq, 4*n_embd]
# project back down:投影回n_embd
x = linear(a, **c_proj) # [n_seq, 4*n_embd] -> [n_seq, n_embd]
return x
这里仅仅是升维再降维,具体地将n_embd投影到一个更高的维度4*n_embd,然后再将其投影回n_embd。
多头因果自注意力
这里将通过分别解释“多头因果自注意力”的每个词,来一步步理解“多头因果自注意力”:
- 注意力(Attention)
- 自(Self)
- 因果(Causal)
- 多头(Multi-Head)
缩放点积注意力(scaled dot-product attention)
其中,查询向量\(\mathbf Q\in\mathbb R^{T\times d}\)、 键向量\(\mathbf K \in\mathbb R^{T\times d}\)、值向量\(\mathbf V\in\mathbb R^{T\times d}\),\(T\)为序列长度。
注意力得分除以\(\sqrt{d}\)进行缩放, 是考虑到在\(d\)过大时,点积值较大会使得后续Softmax操作溢出导致梯度爆炸,不利于模型优化。
def attention_raw(q, k, v):
""" 原始缩放点积注意力实现
输入输出tensor形状: [n_q, d_k], [n_k, d_k], [n_k, d_v] -> [n_q, d_v]
params:
q: np.ndarray[n_seq, n_embd], 查询向量
k: np.ndarray[n_seq, n_embd], 键向量
v: np.ndarray[n_seq, n_embd], 值向量
"""
return softmax(q @ k.T / np.sqrt(q.shape[-1])) @ v
# 以通过对q、k、v进行投影变换来增强自注意效果
def self_attention_raw(x, w_k, w_q, w_v, w_proj):
""" 自注意力原始实现
输入输出tensor形状: [n_seq, n_embd] -> [n_seq, n_embd]
params:
x: np.ndarray[n_seq, n_embd], 输入token嵌入序列
w_k: np.ndarray[n_embd, n_embd], 查询向量投影层参数
w_q: np.ndarray[n_embd, n_embd], 键向量投影层参数
w_v: np.ndarray[n_embd, n_embd], 值向量投影层参数
w_proj: np.ndarray[n_embd, n_embd], 自注意力输出投影层参数
"""
# qkv projections
q = x @ w_k # [n_seq, n_embd] @ [n_embd, n_embd] -> [n_seq, n_embd]
k = x @ w_q # [n_seq, n_embd] @ [n_embd, n_embd] -> [n_seq, n_embd]
v = x @ w_v # [n_seq, n_embd] @ [n_embd, n_embd] -> [n_seq, n_embd]
# perform self attention
x = attention(q, k, v) # [n_seq, n_embd] -> [n_seq, n_embd]
# out projection
x = x @ w_proj # [n_seq, n_embd] @ [n_embd, n_embd] -> [n_seq, n_embd]
return x
# 将w_q、w_k和w_v组合成一个单独的矩阵w_fc,执行投影操作,然后拆分结果,我们就可以将矩阵乘法的数量从4个减少到2个
def self_attention(x, c_attn, c_proj):
""" 自注意力优化后实现(w_q 、w_k 、w_v合并成一个矩阵w_fc进行投影,再拆分结果)
同时GPT-2的实现:加入偏置项参数(所以使用线性层,进行仿射变换)
输入输出tensor形状: [n_seq, n_embd] -> [n_seq, n_embd]
params:
x: np.ndarray[n_seq, n_embd], 输入token嵌入序列
w_fc: np.ndarray[n_embd, 3*n_embd], 查询向量投影层参数
w_proj: np.ndarray[n_embd, n_embd], 自注意力输出投影层参数
"""
# qkv projections
x = linear(x, **c_attn) # [n_seq, n_embd] -> [n_seq, 3*n_embd]
# split into qkv
q, k, v = np.split(x, 3, axis=-1) # [n_seq, 3*n_embd] -> 3 of [n_seq, n_embd]
# perform self attention
x = attention(q, k, v) # [n_seq, n_embd] -> [n_seq, n_embd]
# out projection
x = linear(x, **c_proj) # [n_seq, n_embd] @ [n_embd, n_embd] = [n_seq, n_embd]
return x
因果
为了防止序列建模时出现信息泄露,需要修改注意力矩阵(增加Mask)以隐藏或屏蔽我们的输入,从而避免模型在训练阶段直接看到后续的文本序列(信息泄露)进而无法得到有效地训练。
# 输入是 ["not", "all", "heroes", "wear", "capes"]
# 原始自注意力
not all heroes wear capes
not 0.116 0.159 0.055 0.226 0.443
all 0.180 0.397 0.142 0.106 0.175
heroes 0.156 0.453 0.028 0.129 0.234
wear 0.499 0.055 0.133 0.017 0.295
capes 0.089 0.290 0.240 0.228 0.153
# 因果自注意力 (行为j, 列为i)
# 为防止输入的所有查询都能预测未来,需要将所有j>i位置设置为0 :
not all heroes wear capes
not 0.116 0. 0. 0. 0.
all 0.180 0.397 0. 0. 0.
heroes 0.156 0.453 0.028 0. 0.
wear 0.499 0.055 0.133 0.017 0.
capes 0.089 0.290 0.240 0.228 0.153
# 在应用 softmax 之前,我们需要修改我们的注意力矩阵,得到掩码自注意力
# 即,在softmax之前将要屏蔽项的注意力得分设置为 −∞(归一化系数为0)
# mask掩码矩阵
0 -1e10 -1e10 -1e10 -1e10
0 0 -1e10 -1e10 -1e10
0 0 0 -1e10 -1e10
0 0 0 0 -1e10
0 0 0 0 0
使用 -1e10 而不是 -np.inf ,因为 -np.inf 可能会导致 nans
加入掩码矩阵的注意力实现:
def attention(q, k, v, mask):
""" 缩放点积注意力实现
输入输出tensor形状: [n_q, d_k], [n_k, d_k], [n_k, d_v] -> [n_q, d_v]
params:
q: np.ndarray[n_seq, n_embd], 查询向量
k: np.ndarray[n_seq, n_embd], 键向量
v: np.ndarray[n_seq, n_embd], 值向量
mask: np.ndarray[n_seq, n_seq], 注意力掩码矩阵
"""
return softmax(q @ k.T / np.sqrt(q.shape[-1]) + mask) @ v
因果注意力掩码矩阵可视化
x = np.array([1, 1, 1, 1, 1])
causal_mask = (1 - np.tri(x.shape[0], dtype=x.dtype))* -1e10
print(causal_mask)
plotHot(causal_mask)
[[-0.e+00 -1.e+10 -1.e+10 -1.e+10 -1.e+10]
[-0.e+00 -0.e+00 -1.e+10 -1.e+10 -1.e+10]
[-0.e+00 -0.e+00 -0.e+00 -1.e+10 -1.e+10]
[-0.e+00 -0.e+00 -0.e+00 -0.e+00 -1.e+10]
[-0.e+00 -0.e+00 -0.e+00 -0.e+00 -0.e+00]]
注意力Mask可视化
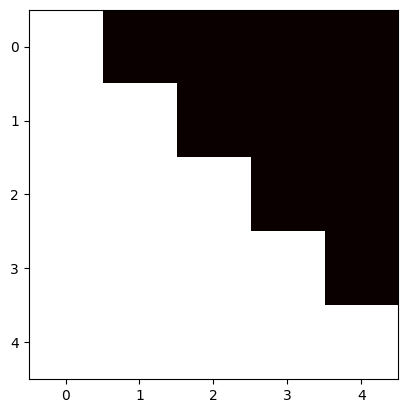
因果注意力的最终实现
def causal_self_attention(x, c_attn, c_proj):
""" 因果自注意力优化后实现(w_q 、w_k 、w_v合并成一个矩阵w_fc进行投影,再拆分结果)
同时GPT-2的实现:加入偏置项参数(所以使用线性层,进行仿射变换)
输入输出tensor形状: [n_seq, n_embd] -> [n_seq, n_embd]
params:
x: np.ndarray[n_seq, n_embd], 输入token嵌入序列
c_attn: np.ndarray[n_embd, 3*n_embd], 查询向量投影层参数
c_proj: np.ndarray[n_embd, n_embd], 自注意力输出投影层参数
"""
# qkv projections
x = linear(x, **c_attn) # [n_seq, n_embd] -> [n_seq, 3*n_embd]
# split into qkv
q, k, v = np.split(x, 3, axis=-1) # [n_seq, 3*n_embd] -> 3 of [n_seq, n_embd]
# causal mask to hide future inputs from being attended to
causal_mask = (1 - np.tri(x.shape[0], dtype=x.dtype))* -1e10 # [n_seq, n_seq]
# perform causal self attention
x = attention(q, k, v, causal_mask) # [n_seq, n_embd] -> [n_seq, n_embd]
# out projection
x = linear(x, **c_proj) # [n_seq, n_embd] @ [n_embd, n_embd] = [n_seq, n_embd]
return x
实际,用\(-1e10\)替换-np.inf, 因为-np.inf会导致nans错误。
注意力计算矩阵乘法步骤图解:
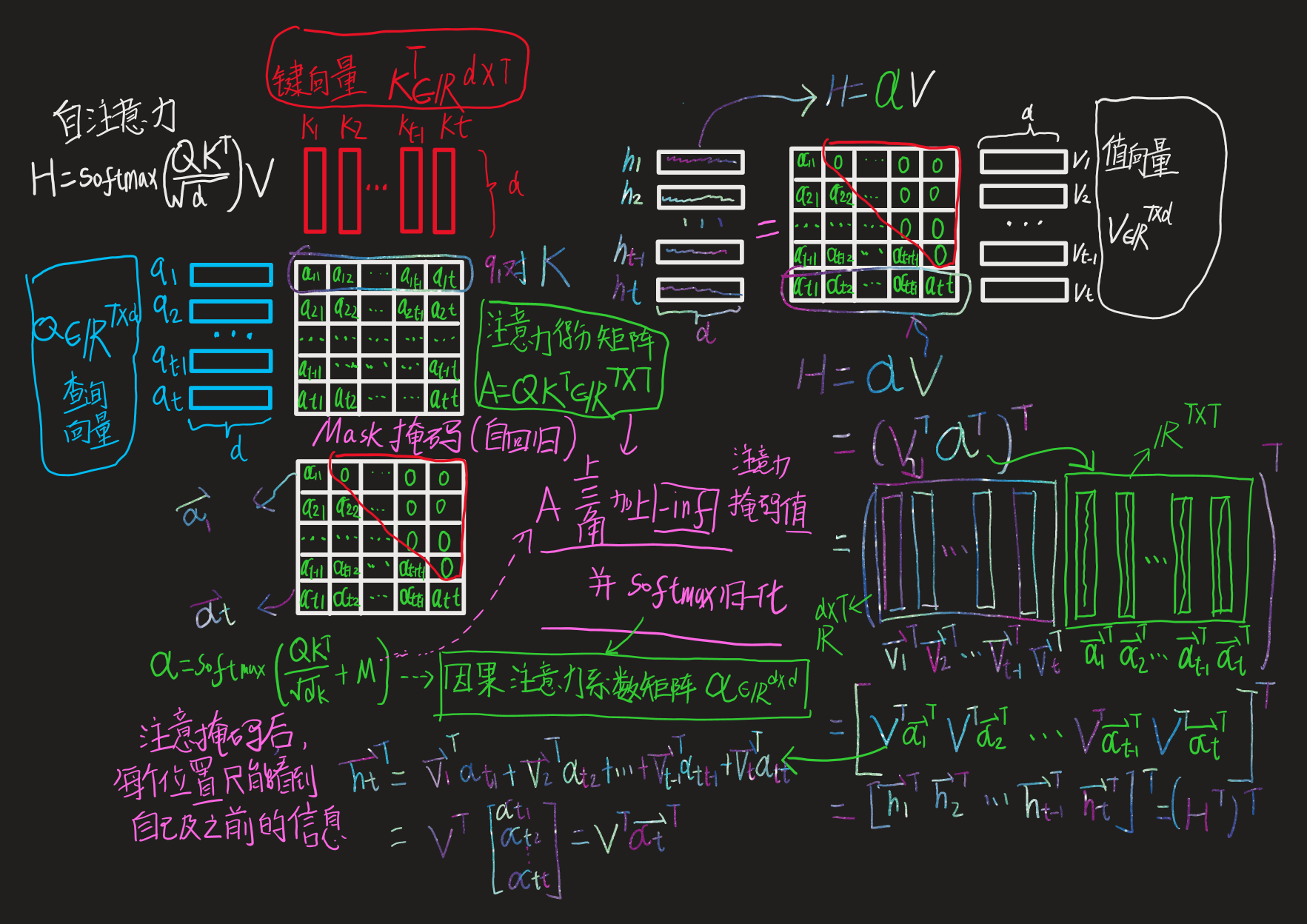
多头自注意力(Multi-Head-self-Attention)
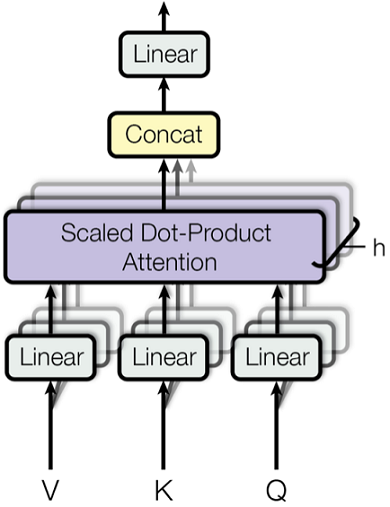
将Q、K、V切分为n_head个,分别计算后(适合并行计算),在合并
def mha(x, c_attn, c_proj, n_head):
""" 多头自注意力实现
输入输出tensor形状: [n_seq, n_embd] -> [n_seq, n_embd]
每个注意力计算的维度从n_embd降低到 n_embd/n_head。
通过降低维度,模型利用多个子空间进行建模
params:
x: np.ndarray[n_seq, n_embd], 输入token嵌入序列
c_attn: np.ndarray[n_embd, 3*n_embd], 查询向量投影层参数
c_proj: np.ndarray[n_embd, n_embd], 自注意力输出投影层参数
"""
# qkv投影变换
x = linear(x, **c_attn) # [n_seq, n_embd] -> [n_seq, 3*n_embd]
# 划分为qkv
qkv = np.split(x, 3, axis=-1) # [n_seq, 3*n_embd] -> [3, n_seq, n_embd]
# 将n_embd继续划分为_head个注意力头
qkv_heads = list(map(lambda x: np.split(x, n_head, axis=-1), qkv)) # [3, n_seq, n_embd] -> [3, n_head, n_seq, n_embd/n_head]
# 构造causal mask矩阵
causal_mask = (1 - np.tri(x.shape[0], dtype=x.dtype))* -1e10 # [n_seq, n_seq]
# 单独执行每个头的因果自注意力(可多核多线程并行执行)
out_heads = [attention(q, k, v, causal_mask) for q, k, v in zip(*qkv_heads)] # [3, n_head, n_seq, n_embd/n_head] -> [n_head, n_seq, n_embd/n_head]
# 合并多个heads的结果
x = np.hstack(out_heads) # [n_head, n_seq, n_embd/n_head] -> [n_seq, n_embd]
# 多头因果自注意力输出projection
x = linear(x, **c_proj) # [n_seq, n_embd] -> [n_seq, n_embd]
return x
将所有代码组合起来
main函数为推理代码,其流程为:加载分词器和模型,对输入分词,然后预测,最后将预测的词元id解码为文本
def main(prompt: str, n_tokens_to_generate: int=40, model_size: str="124M", models_dir: str="models"):
from utils import load_encoder_hparams_and_params
# 从open-ai的gpt-2文件中加载f分词器encoder、超参数hparams和模型参数params
encoder, hparams, params = load_encoder_hparams_and_params(model_size, models_dir)
# 使用BPE Tokenizer将输入文本编码为Token Ids
input_ids = encoder.encode(prompt)
assert len(input_ids) + n_tokens_to_generate < hparams["n_ctx"]
# 调用generate函数, 输出预测的Token Ids
output_ids = generate(input_ids, params, hparams["n_head"], n_tokens_to_generate)
# 将output_ids解码为文本
output_text = encoder.decode(output_ids)
return output_text
将所有代码组合起来就得到了gpt2.py,总共的代码只有120行(如果移除注释、空格之类的,那就只有60行)。
架构改进
停止生成
当前实现需要事先指定要生成的确切token数量n_tokens_to_generate。这并不是一个很好的方法,因为生成的文本不一定符合要求,要么太长、太短,不是一个完整的句子。
为了解决这个问题,可以引入一个特殊的句子结束token EOS。在预训练期间,输入的末尾附加EOS token(比如,tokens = ["not", "all", "heroes", "wear", "capes", ".", "<|EOS|>"])。在生成过程中,只需要在遇到EOS token时停止(或者达到最大序列长度):
def generate(inputs, eos_id, max_seq_len):
prompt_len = len(inputs)
while inputs[-1] != eos_id and len(inputs) < max_seq_len:
output = gpt(inputs)
next_id = np.argmax(output[-1])
inputs.append(int(next_id))
return inputs[prompt_len:]
GPT-2没有使用 EOS token进行预训练,因此无法在我们的代码中使用这种方法,但现在大多数 LLMs 都已经使用 EOS token了。
无条件生成
使用当前模型生成文本需要提供输入。但是我们也可以让模型执行无条件生成,即模型在没有任何输入时生成文本。
无条件生成不是特别有用,但它是演示GPT能力的一种有趣方式。
这是通过在预训练期间在输入开头加上一个特殊的句子开头token (BOS)来实现的(例如 tokens = ["<|BOS|>", "not", "all", "heroes", "wear", "capes", "."])。要进行无条件文本生成的话,仅需输入一个包含BOS token的列表:
def generate_unconditioned(bos_id, n_tokens_to_generate):
inputs = [bos_id]
for _ in range(n_tokens_to_generate):
output = gpt(inputs)
next_id = np.argmax(output[-1])
inputs.append(int(next_id))
return inputs[1:]
GPT-2的预训练是带有BOS token的(不过它有一个令人困惑的名字<|endoftext|>),因此在我们的实现中要运行无条件生成的话,只需要简单地将这行代码更改为:
input_ids = encoder.encode(prompt) if prompt else [encoder.encoder["<|endoftext|>"]]
然后运行,
python gpt2.py ""
然后即可生成:
The first time I saw the new version of the game, I was so excited. I was so excited to see the new version of the game, I was so excited to see the new version
因为使用的是贪心采样,所以输出结果不是很好(重复的内容较多),而且每次运行代码的结果都是确定的。为了获得更高质量的、不确定性更大的生成结果,可以直接从概率分布中进行采样(Top-k截断后进行采样)。
二、项目实战
将仓库clone下来(本文在colab上运行),安装依赖:
%git clone https://github.com/jaymody/picoGPT
%cd picoGPT
%pip install -r requirements.txt
项目主要文件:
- encoder.py 包含了OpenAI的BPE分词器的代码,直接从gpt-2仓库拿过来的
- utils.py 包含下载并加载GPT-2模型的权重,分词器和超参数
- gpt2.py 包含了实际GPT模型和生成的代码,可以作为脚本运行
效果展示
下载预训练GPT2模型
from utils import load_encoder_hparams_and_params
encoder, hparams, params = load_encoder_hparams_and_params("124M", "models")
Fetching checkpoint: 1.00kb [00:00, 4.65Mb/s]
Fetching encoder.json: 1.04Mb [00:01, 846kb/s]
Fetching hparams.json: 1.00kb [00:00, 4.18Mb/s]
Fetching model.ckpt.data-00000-of-00001: 498Mb [00:39, 12.7Mb/s]
Fetching model.ckpt.index: 6.00kb [00:00, 4.19Mb/s]
Fetching model.ckpt.meta: 472kb [00:00, 545kb/s]
Fetching vocab.bpe: 457kb [00:00, 619kb/s]
在picoGPT的models/124M下,有如下文件:
checkpoint hparams.json model.ckpt.index vocab.bpe
encoder.json model.ckpt.data-00000-of-00001 model.ckpt.meta
查看超参数
hparams
{'n_vocab': 50257, 'n_ctx': 1024, 'n_embd': 768, 'n_head': 12, 'n_layer': 12}
编码器
ids = encoder.encode("Alan Turing theorized that computers")
ids
[36235, 39141, 18765, 1143, 326, 9061]
分词得到的Token(本质上,是将word分割为sub-word,以word为处理单位)
[encoder.decoder.get(tk) for tk in ids]
['Alan', 'ĠTuring', 'Ġtheor', 'ized', 'Ġthat', 'Ġcomputers']
encoder.decode(ids)
"Alan Turing theorized that computers"
词汇表以及决定字符串如何分解的字节对组合(byte-pair merges),是通过训练分词器获得的。加载分词器,就会从encoder.json词汇表和vocab.bpe字节对组合中加载。
GPT预测
python gpt2.py "Alan Turing theorized that computers" --n_tokens_to_generate 20
could be used to solve problems in a way that was not possible with human brains.
权重加载
GPT2权重下载和参数加载
import json
import os
import re
import numpy as np
import requests
import tensorflow as tf
from tqdm import tqdm
from encoder import get_encoder
# 通过给定的 model_size 和 model_dir,从特定URL下载GPT-2模型文件。
def download_gpt2_files(model_size, model_dir):
assert model_size in ["124M", "355M", "774M", "1558M"]
file_names = ["checkpoint","encoder.json","hparams.json","model.ckpt.data-00000-of-00001","model.ckpt.index","model.ckpt.meta","vocab.bpe"]
for filename in file_names:
url = "https://openaipublic.blob.core.windows.net/gpt-2/models"
r = requests.get(f"{url}/{model_size}/{filename}", stream=True)
r.raise_for_status()
with open(os.path.join(model_dir, filename), "wb") as f:
file_size = int(r.headers["content-length"])
chunk_size = 1000
with tqdm(ncols=100, desc="Fetching " + filename, total=file_size, unit_scale=True, unit="b") as pbar:
# 1k for chunk_size, since Ethernet packet size is around 1500 bytes
for chunk in r.iter_content(chunk_size=chunk_size):
f.write(chunk)
pbar.update(chunk_size)
该函数从给定的 TensorFlow CheckPoint文件 tf_ckpt_path 和 GPT-2 模型参数 hparams 中加载 GPT-2 模型的参数。
def load_gpt2_params_from_tf_ckpt(tf_ckpt_path, hparams):
# 根据变量名的特征,将加载的参数值组织成一个嵌套字典,对应于 GPT-2模型的层次结构, 并返回
def set_in_nested_dict(d, keys, val):
if not keys:
return val
if keys[0] not in d:
d[keys[0]] = {}
d[keys[0]] = set_in_nested_dict(d[keys[0]], keys[1:], val)
return d
# 建一个字典 params,其中包含键为 "blocks",值为长度为 hparams["n_layer"]
params = {"blocks": [{} for _ in range(hparams["n_layer"])]}
for name, _ in tf.train.list_variables(tf_ckpt_path):
array = np.squeeze(tf.train.load_variable(tf_ckpt_path, name))
name = name[len("model/") :]
if name.startswith("h"):
m = re.match(r"h([0-9]+)/(.*)", name)
n = int(m[1])
sub_name = m[2]
set_in_nested_dict(params["blocks"][n], sub_name.split("/"), array)
else:
set_in_nested_dict(params, name.split("/"), array)
return params
tf从原始的OpenAI TensorFlow checkpoint加载的参数
tf.train.list_variables(tf_ckpt_path)返回参数结构元组的列表
[('model/h0/attn/c_attn/b', [2304]),
('model/h0/attn/c_attn/w', [1, 768, 2304]),
('model/h0/attn/c_proj/b', [768]),
('model/h0/attn/c_proj/w', [1, 768, 768]),
('model/h0/ln_1/b', [768]),
('model/h0/ln_1/g', [768]),
('model/h0/ln_2/b', [768]),
('model/h0/ln_2/g', [768]),
('model/h0/mlp/c_fc/b', [3072]),
('model/h0/mlp/c_fc/w', [1, 768, 3072]),
('model/h0/mlp/c_proj/b', [768]),
('model/h0/mlp/c_proj/w', [1, 3072, 768]),
...
('model/h11/attn/c_attn/b', [2304]),
('model/h11/attn/c_attn/w', [1, 768, 2304]),
('model/h11/attn/c_proj/b', [768]),
('model/h11/attn/c_proj/w', [1, 768, 768]),
('model/h11/ln_1/b', [768]),
('model/h11/ln_1/g', [768]),
('model/h11/ln_2/b', [768]),
('model/h11/ln_2/g', [768]),
('model/h11/mlp/c_fc/b', [3072]),
('model/h11/mlp/c_fc/w', [1, 768, 3072]),
('model/h11/mlp/c_proj/b', [768]),
('model/h11/mlp/c_proj/w', [1, 3072, 768]),
('model/ln_f/b', [768]),
('model/ln_f/g', [768]),
('model/wpe', [1024, 768]),
('model/wte', [50257, 768])]
load_variable函数加载模型对应模块的参数(从模型的二进制编码参数文件中,将对应参数加载为numpy的ndarray)
load_variable(ckpt_dir_or_file, name)
Returns the tensor value of the given variable in the checkpoint.
Args:
ckpt_dir_or_file: Directory with checkpoints file or path to checkpoint.
name: Name of the variable to return.
Returns:
A numpy `ndarray` with a copy of the value of this variable.
查看3个示例
>>> tf.train.load_variable(tf_ckpt_path, 'model/h10/attn/c_attn/w').shape
(1, 768, 2304)
>>> np.squeeze(tf.train.load_variable(tf_ckpt_path, 'model/h6/mlp/c_fc/w')).shape
(768, 3072)
>>> tf.train.load_variable(tf_ckpt_path, 'model/wte').shape
(50257, 768)
加载并返回GPT-2模型的编码器(encoder)、超参数(hparams)和参数(params
def load_encoder_hparams_and_params(model_size, models_dir):
assert model_size in ["124M", "355M", "774M", "1558M"]
model_dir = os.path.join(models_dir, model_size)
tf_ckpt_path = tf.train.latest_checkpoint(model_dir)
# 如果在models_dir中找不到 GPT-2 模型文件,则会调用 download_gpt2_files 函数下载这些文件
if not tf_ckpt_path: # download files if necessary
os.makedirs(model_dir, exist_ok=True)
download_gpt2_files(model_size, model_dir)
tf_ckpt_path = tf.train.latest_checkpoint(model_dir)
encoder = get_encoder(model_size, models_dir)
hparams = json.load(open(os.path.join(model_dir, "hparams.json")))
# 模型参数
params = load_gpt2_params_from_tf_ckpt(tf_ckpt_path, hparams)
return encoder, hparams, params
看一下参数结构
import numpy as np
def shape_tree(d):
if isinstance(d, np.ndarray):
return list(d.shape)
elif isinstance(d, list):
return [shape_tree(v) for v in d]
elif isinstance(d, dict):
return {k: shape_tree(v) for k, v in d.items()}
else:
ValueError("uh oh")
shape_tree(params) # 递归打印
blocks里面装了12个dncoder的参数
{'blocks':
[{'attn': {'c_attn': {'b': [2304], 'w': [768, 2304]},
'c_proj': {'b': [768], 'w': [768, 768]}},
'ln_1': {'b': [768], 'g': [768]},
'ln_2': {'b': [768], 'g': [768]},
'mlp': {'c_fc': {'b': [3072], 'w': [768, 3072]},
'c_proj': {'b': [768], 'w': [3072, 768]}}},
{'attn': {'c_attn': {'b': [2304], 'w': [768, 2304]},
'c_proj': {'b': [768], 'w': [768, 768]}},
'ln_1': {'b': [768], 'g': [768]},
'ln_2': {'b': [768], 'g': [768]},
'mlp': {'c_fc': {'b': [3072], 'w': [768, 3072]},
'c_proj': {'b': [768], 'w': [3072, 768]}}},
...
{'attn': {'c_attn': {'b': [2304], 'w': [768, 2304]},
'c_proj': {'b': [768], 'w': [768, 768]}},
'ln_1': {'b': [768], 'g': [768]},
'ln_2': {'b': [768], 'g': [768]},
'mlp': {'c_fc': {'b': [3072], 'w': [768, 3072]},
'c_proj': {'b': [768], 'w': [3072, 768]}}}],
'ln_f': {'b': [768], 'g': [768]},
'wpe': [1024, 768],
'wte': [50257, 768]}
为了对比,这里显示了params的形状,但是数字被hparams替代:
{
"wpe": [n_ctx, n_embd],
"wte": [n_vocab, n_embd],
"ln_f": {"b": [n_embd], "g": [n_embd]},
"blocks": [
{
"attn": {
"c_attn": {"b": [3*n_embd], "w": [n_embd, 3*n_embd]},
"c_proj": {"b": [n_embd], "w": [n_embd, n_embd]},
},
"ln_1": {"b": [n_embd], "g": [n_embd]},
"ln_2": {"b": [n_embd], "g": [n_embd]},
"mlp": {
"c_fc": {"b": [4*n_embd], "w": [n_embd, 4*n_embd]},
"c_proj": {"b": [n_embd], "w": [4*n_embd, n_embd]},
},
},
... # repeat for n_layers
]
}
Tokenizer分词器
BPE分词算法原理
核心思想,就是构造sub-word(子词)来处理OOV(Out of Vocabulary Words),即用子词来处理:未登录词和稀有词。
算法直接将传统的压缩算法BPE,用到分词上。思路就是:迭代地将语料中最高频一对byte(字符) <'A', 'B'>合并(替换)为<'AB'>,直到到达指定合并次数(或指定词表大小)。
首先初始化词表vocab为语料中的字符集合,统计词频(例如英文进行空格分割后统计),然后经过上述流程不断更新pair频率和词表。
这样,最终的词表是由初始的字符集以及高频的字符pair构成,这样可以实现对语料的压缩,减少需要编码token的数量,同时又能处理oov。
后续将专门开一篇文章来讲解Tokenizer的实现,包括BPE、WordPiece(在BPE的基础上,获取语言模型,基于似然最大的字符pair来进行合并)和SentencePiece(一种语言无关的Unicode格式 分词框架,将空格表示为特殊的字符,从而可以处理多语言语料,并使用了优先队列进行算法优化,复杂度为O(Nlog(N)))
在语料上训练后,将得到Tokenizer的sub-word集合即词表,vocab问题。而,encoder.json中则存放Tokenizer的配置参数
encoder.py代码
"""Byte pair encoding utilities.
Copied from: https://github.com/openai/gpt-2/blob/master/src/encoder.py.
"""
import json
import os
from functools import lru_cache
import regex as re
@lru_cache()
def bytes_to_unicode():
"""
Returns list of utf-8 byte and a corresponding list of unicode strings.
The reversible bpe codes work on unicode strings.
This means you need a large # of unicode characters in your vocab if you want to avoid UNKs.
When you're at something like a 10B token dataset you end up needing around 5K for decent coverage.
This is a significant percentage of your normal, say, 32K bpe vocab.
To avoid that, we want lookup tables between utf-8 bytes and unicode strings.
And avoids mapping to whitespace/control characters the bpe code barfs on.
"""
bs = list(range(ord("!"), ord("~") + 1)) + list(range(ord("¡"), ord("¬") + 1)) + list(range(ord("®"), ord("ÿ") + 1))
cs = bs[:]
n = 0
for b in range(2**8):
if b not in bs:
bs.append(b)
cs.append(2**8 + n)
n += 1
cs = [chr(n) for n in cs]
return dict(zip(bs, cs))
def get_pairs(word):
"""Return set of symbol pairs in a word.
Word is represented as tuple of symbols (symbols being variable-length strings).
"""
pairs = set()
prev_char = word[0]
for char in word[1:]:
pairs.add((prev_char, char))
prev_char = char
return pairs
class Encoder:
def __init__(self, encoder, bpe_merges, errors="replace"):
self.encoder = encoder
self.decoder = {v: k for k, v in self.encoder.items()}
self.errors = errors # how to handle errors in decoding
self.byte_encoder = bytes_to_unicode()
self.byte_decoder = {v: k for k, v in self.byte_encoder.items()}
self.bpe_ranks = dict(zip(bpe_merges, range(len(bpe_merges))))
self.cache = {}
# Should have added re.IGNORECASE so BPE merges can happen for capitalized versions of contractions
self.pat = re.compile(r"""'s|'t|'re|'ve|'m|'ll|'d| ?\p{L}+| ?\p{N}+| ?[^\s\p{L}\p{N}]+|\s+(?!\S)|\s+""")
def bpe(self, token):
if token in self.cache:
return self.cache[token]
word = tuple(token)
pairs = get_pairs(word)
if not pairs:
return token
while True:
bigram = min(pairs, key=lambda pair: self.bpe_ranks.get(pair, float("inf")))
if bigram not in self.bpe_ranks:
break
first, second = bigram
new_word = []
i = 0
while i < len(word):
try:
j = word.index(first, i)
new_word.extend(word[i:j])
i = j
except:
new_word.extend(word[i:])
break
if word[i] == first and i < len(word) - 1 and word[i + 1] == second:
new_word.append(first + second)
i += 2
else:
new_word.append(word[i])
i += 1
new_word = tuple(new_word)
word = new_word
if len(word) == 1:
break
else:
pairs = get_pairs(word)
word = " ".join(word)
self.cache[token] = word
return word
def encode(self, text):
bpe_tokens = []
for token in re.findall(self.pat, text):
token = "".join(self.byte_encoder[b] for b in token.encode("utf-8"))
bpe_tokens.extend(self.encoder[bpe_token] for bpe_token in self.bpe(token).split(" "))
return bpe_tokens
def decode(self, tokens):
text = "".join([self.decoder[token] for token in tokens])
text = bytearray([self.byte_decoder[c] for c in text]).decode("utf-8", errors=self.errors)
return text
加载tokenier数据,获取分词器
def get_encoder(model_name, models_dir):
with open(os.path.join(models_dir, model_name, "encoder.json"), "r") as f:
encoder = json.load(f)
with open(os.path.join(models_dir, model_name, "vocab.bpe"), "r", encoding="utf-8") as f:
bpe_data = f.read()
bpe_merges = [tuple(merge_str.split()) for merge_str in bpe_data.split("\n")[1:-1]]
return Encoder(encoder=encoder, bpe_merges=bpe_merges)


