Codeforces Round #506 (Div. 3)ABCDEF

并没有参加比赛，全是赛后AC

A题

　　题意：现有一个长度为n的字符串s。你需要构建一个长度最小的字符串t，使得t中恰好包含k个s（允许部分重叠），输出这个字符串

 

　　

/*
    我们可以非常容易的发现我们构造出来的字符串t有着鲜明的特征。即t中有大量重复的子串，可以证明的是t = S + (K-1)*A， A是S串中删去一段字符串（这段字符串满足既是S的前缀又是S的后缀）。
*/
#include<cstdio>
#include<iostream>

using namespace std;

const int maxn = 50 + 5;

char a[maxn];
int n, k;

int main(void) {
    scanf("%d%d", &n, &k);
    scanf("%s", a + 1);
    string s1 = "", s2 = ""; int res = 0;
    for (int i = 1, j = n; i < n; ++ i, -- j) {
        s1 = s1 + a[i];
        s2 = a[j] + s2;
        if (s1 == s2) res = max(res, i);
    }
    int len = n - res; 
//    cout << len << endl;
    string ans = "";
    for (int i = n; i >= n - len + 1; -- i) ans = a[i] + ans;
    for (int i = 1; i <= n; ++ i) printf("%c", a[i]);
    for (int i = 1; i < k; ++ i) cout << ans; puts("");
    return 0;
}

 

B题

　　题意：给出一个长度为n的数组A，数组A中的元素a[i]满足（1<=a[i]<=10^9），且a[i]严格大于a[i-1](2<=i<=n)。现在要你找出一个数组B，满足数组B中所有元素在A中都是有序排列的，即B是A的非连续子序列，数组B中的元素要满足b[i]>=2*b[i-1]，输出这个数组B的最大长度。

/*
一个类似导弹拦截的DP+决策单调性优化（这个优化由单调队列实现）
*/
#include<cstdio>
#include<algorithm>

using namespace std;

const int maxn = 2e5 + 5;

int n, a[maxn], f[maxn], Stack[maxn], val[maxn];


int main(void) {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++ i) scanf("%d", &a[i]);
    int L = 1, R = 1;
    Stack[1] = 1;
    val[1] = 1;
    int ans = 1;
    // a值小f值大 和 a值大f值小 
    for (int i = 2; i <= n; ++ i) {
        while (L <= R && a[Stack[L]] * 2 < a[i]) ++ L;
        if (L <= R) {
            int cur = val[L] + 1;
            ans = max(ans, cur);
            while (L <= R && cur >= val[R]) -- R;
            ++ R; Stack[R] = i; val[R] = cur;        
        } else {
            int cur = 1;
            ++ R; Stack[R] = i; val[R] = cur;
        }
    }
    printf("%d\n", ans);
    return 0;
}

 

C题：

　　题意：给出n个区间（2<=n<=3e5）,区间的左右边界均在[0,1e9]之间，现要你去掉一个区间，求出剩下n-1个区间的区间交，使得这个区间交的长度最大。输出这个长度

 

/*
    我们维护两个东西，一个是区间并的前缀f[i]，另一个是区间并的后缀g[i]。如果我们去掉i这个区间，答案就是f[i-1]这个区间和g[i+1]这个区间的区间并。
    
*/
#include<bits/stdc++.h>

using namespace std;

const int maxn = 3e5 + 5;

int n, l[maxn], r[maxn];

struct node {
    int l, r;
} f[maxn], g[maxn];

pair<int, int> Make(int l0, int r0, int l1, int r1) {
    if (l0 > l1) {
        swap(l0, l1); swap(r0, r1);
    }
    // [l0, r0] [l1, r1]  l0 <= l1
    if (r0 <= l1) return make_pair(-1, -1);
    if (r0 >= r1) return make_pair(l1, r1);
    return make_pair(l1, r0);
} // 输入两个区间，返回他们的并区间

int Get_Ans(pair<int, int> tmp) {
    return tmp.second - tmp.first;
} //得到区间tmp的长度。

int main(void) {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++ i) scanf("%d%d", &l[i], &r[i]);
    
    int L = l[1], R = r[1];
    f[1].l = L; f[1].r = R;
    for (int i = 2; i <= n; ++ i) {
        pair<int, int> tmp = Make(L, R, l[i], r[i]);
        L = f[i].l = tmp.first;    R = f[i].r = tmp.second;
    }
    
    L = l[n]; R = r[n];
    g[n].l = L; g[n].r = R;
    for (int i = n - 1; i >= 1; -- i) {
        pair<int, int> tmp = Make(L, R, l[i], r[i]);
        L = g[i].l = tmp.first; R = g[i].r = tmp.second;
    }
    
    int ans = max(Get_Ans(make_pair(g[2].l, g[2].r)), Get_Ans(make_pair(f[n - 1].l, f[n - 1].r)));
    
    for (int i = 2; i < n; ++ i) {
        ans = max(ans, Get_Ans(Make(f[i - 1].l, f[i - 1].r, g[i + 1].l, g[i + 1].r)));
    }
    printf("%d\n", ans);
    return 0;
}

 

D题：

　　题意：给出一个长度为n的数组A和一个k，满足1<=n<= 2e5, 2<=k<=1e9,1<=a[i]<=1e9。现在你可以拿出A数组里面的两个数字a[i]和a[j]（i！=j），将a[i]和a[j]拼在一起形成一个大数（例如5和123拼在一起可以拼出5123）如果这个拼成的大数是k的倍数，那么++ Ans。要求输出Ans。

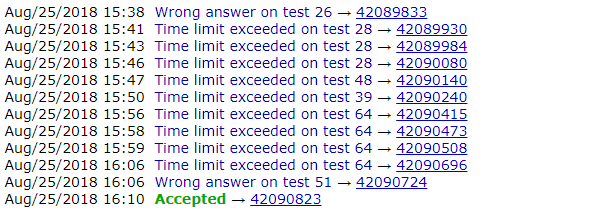
　　我好菜啊：

 

/*
这题我。。。唉。（因为某个智障错误我的代码比别人的代码慢了20%，T了11发才发现。。）
思路：我们考虑连接好的大数x，可以发现x%k==0这个条件等价于把x减去好多好多的k，直到把x减到0为止。于是乎，我们就发现了一个算法，就是我们把a[i]*（10^(a[j]的长度)）对K取模，得到一个小于k的数字x2，
然后在把a[j]对k取模，得到一个小于k的数字y2。那么（x2+y2）%k等价于原来的大数%k。我们这么处理后就可以用map来维护这个东西。计算答案就简单啦。
    智障错误是：我计算i的时候为了防止a[i]和a[i]拼在一起的情况出现，直接在map里面消除了a[i]的影响，算完后再加上去，这个操作复杂度是log的还带上一个巨大的常数，结果就T了几百ms，别人算法的这个操作都是O(1)的。。。。我好菜啊
*/
#pragma GCC diagnostic error "-std=c++11"
#pragma GCC target("avx")
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")
#include<iostream>
#include<cstdio>
#include<map>
#define ll long long
#define LG 32
#define N 200100
using namespace std;

ll n,m,ten[40],num[N],ans;
map<ll,ll>cnt[40];

inline ll ws(ll u){ll res=0;for(;u;u/=10) res++;return res;}

int main()
{
    ll i,j,p,q;
    cin>>n>>m;
    ten[0]=1;
    for(i=1;i<=LG;i++) ten[i]=ten[i-1]*10%m;
    for(i=1;i<=n;i++)
    {
        scanf("%lld",&num[i]);
        cnt[ws(num[i])][num[i]%m]++;
    }
    for(i=1;i<=n;i++)
    {
        p=num[i];
        for(j=1;j<=LG;j++)
        {
            p=p*10%m;
            if(cnt[j].count((m-p)%m))
                ans+=cnt[j][(m-p)%m];
        }
        if((num[i]*ten[ws(num[i])]+num[i])%m==0) ans--;
    }
    cout<<ans;
}

 

E题：

　　题意：给出一个节点数量为n的树，边权都为1,。然后定义dis[i]为i号节点到1号节点的最短路径的距离。然后有一个加边的操作，你可以随意连接两个点，边权为1。显然这个加边操作可以显著缩小某些点的dis值。现问你最少要加几条边才可以让所有的点的dis值全部小于3。输出这个加边操作的最小数量。

/*
这题就是贪心啊，我们可以知道如果我们对这颗树（当然若干次操作后就不是一颗树了）上加一条边，那么这条边的一头一定是1（因为这样最优啊）。然后如果我们设Mx为当前最大的dis值，那么这条边连接的一定是一个dis值为Mx - 1的节点（因为这样最优啊）。于是我们就得到了一个贪心。写得优美点就是下面的程序啦！
*/
#pragma GCC optimize(3)
#include<cstdio>
#include<vector>

using namespace std;

const int maxn = 2e5 + 5;

int n, ans = 0;
vector<int> G[maxn];

int dfs(int x, int fat) {
    int dis = 2;
    for (unsigned i = 0; i < G[x].size(); ++ i) {
        int v = G[x][i]; if (v == fat) continue;
        dis = min(dis, dfs(v, x));
    }
    if (dis == 0 && x != 1 && fat != 1) ++ ans;
    return (dis + 1) % 3;
}

int main(void) {
    scanf("%d", &n);
    for (int i = 1; i < n; ++ i) {
        int x, y; scanf("%d%d", &x, &y);
        G[x].push_back(y);
        G[y].push_back(x);
    }
    dfs(1, 0);
    printf("%d\n", ans);
    return 0;
}

 

F题：

　　题意：现有一面长宽可无线延伸的网格，现要求将aa个格子染成红色，bb个格子染成蓝色。要求染成的图形为矩形，且至少有一种颜色染成了矩形。求染成的图形的最小周长。

 

/*
枚举（a+b）大小的矩形的边长，并暴力判断（注意暴力判断的顺序）能否成立，更新答案。
*/
#include <bits/stdc++.h>

#define forn(i, n) for (int i = 0; i < int(n); i++)

typedef long long li;

using namespace std;

const int N = 1000 * 1000;

int lens[N];
int k;

li solve(li a, li b){
    k = 0;
    for (li i = 1; i * i <= b; ++i)
        if (b % i == 0)
            lens[k++] = i;
    
    li ans = 2 * (a + b) + 2;
    li x = a + b;
    int l = 0;
    for (li i = 1; i * i <= x; ++i){
        if (x % i == 0){
            while (l + 1 < k && lens[l + 1] <= i)
                ++l;
            if (b / lens[l] <= x / i)
                ans = min(ans, (i + x / i) * 2);
        }
    }
    
    return ans;
}

int main() {
    li a, b;
    scanf("%lld%lld", &a, &b);
    printf("%lld\n", min(solve(a, b), solve(b, a)));
    return 0;
}