NOIP2010提高组真题部分整理(没有关押罪犯)
\(NOIP2010\)提高组真题部分整理
\(T1\)机器翻译:
题目背景:
小晨的电脑上安装了一个机器翻译软件,他经常用这个软件来翻译英语文章。
题目描述:
这个翻译软件的原理很简单,它只是从头到尾,依次将每个英文单词用对应的中文含义来替换。对于每个英文单词,软件会先在内存中查找这个单词的中文含义,如果内存中有,软件就会用它进行翻译;如果内存中没有,软件就会在外存中的词典内查找,查出单词的中文含义然后翻译,并将这个单词和译义放入内存,以备后续的查找和翻译。
假设内存中有\(M\)个单元,每单元能存放一个单词和译义。每当软件将一个新单词存入内存前,如果当前内存中已存入的单词数不超过\(M-1\),软件会将新单词存入一个未使用的内存单元;若内存中已存入\(M\)个单词,软件会清空最早进入内存的那个单词,腾出单元来,存放新单词。
假设一篇英语文章的长度为\(N\)个单词。给定这篇待译文章,翻译软件需要去外存查找多少次词典?假设在翻译开始前,内存中没有任何单词。
输入输出格式:
输入格式:
共\(2\)行。每行中两个数之间用一个空格隔开。
第一行为两个正整数\(M,N\),代表内存容量和文章的长度。
第二行为\(N\)个非负整数,按照文章的顺序,每个数(大小不超过\(1000\))代表一个英文单词。文章中两个单词是同一个单词,当且仅当它们对应的非负整数相同。
输出格式:
一个整数,为软件需要查词典的次数。
输入输出样例:
输入样例:
3 7
1 2 1 5 4 4 1
输出样例:
5
说明:
每个测试点\(1s\)
对于\(10\%\)的数据有\(M=1,N≤5\)。
对于\(100\%\)的数据有\(0≤M≤100,0≤N≤1000\)。
整个查字典过程如下:每行表示一个单词的翻译,冒号前为本次翻译后的内存状况:
空:内存初始状态为空。
$1. $$1$:查找单词1并调入内存。
\(2.\) \(1 2\):查找单词\(2\)并调入内存。
\(3.\) \(12\):在内存中找到单词\(1\)。
\(4.\) \(1 2 5\):查找单词\(5\)并调入内存。
$5. $$2 5 4$:查找单词\(4\)并调入内存替代单词\(1\)。
\(6.\)\(2 5 4\):在内存中找到单词\(4\)。
\(7.\)\(5 4 1\):查找单词\(1\)并调入内存替代单词\(2\)。
共计查了\(5\)次词典。
题解:
这道题应该是一道典型的队列题目。用队列来模拟翻译软件内存的调用与存储情况,如果有当前单词,就继续,如果没有,就将当前单词入队。然后根据队列中的元素个数来判断是否要将队尾元素出队。
这道题做完了,我只想总结一下队列的\(STL\)函数:
\(queue<int>q:\) 定义一个\(int\)类型的队列\(p\)
\(q.push(x):\)将元素\(x\)放入队头
\(q.pop():\)弹出队尾元素
\(q.front():\)这个函数的返回值为队头的元素
\(q.back():\)这个函数的返回值为队尾的元素
\(q.empty():\)判断队列是否为空
\(q.size():\)返回队列中的元素个数
代码:
#include<cstdio>
#include<iostream>
#include<queue> //队列的STL函数所必备的头文件
using namespace std;
inline int read()//读入优化(就是传说中的快读)
{
int F=1,num=0;
char c=getchar();
while(!isdigit(c)){if(c=='-') F=-1; c=getchar();}
while(isdigit(c)){num=num*10+c-'0'; c=getchar();}
return num*F;
}
queue<int>q;//定义队列q
bool a[1500];//用a[i]来判断单词i是否在队列中出现过
int n,m;
int ans=0;//查询单词的次数
int main()
{
m=read(),n=read();
for(int i=1;i<=n;++i)//循环读入单词
{
int x=read();
if(a[x]==true) continue;//如果队列中有该单词,就继续读入
else if(q.size()<m)//如果队列中的元素不超过m个,即内存没有满
{
q.push(x);//将这个单词加入队列(加入内存)
ans++;//从外存查询单词的次数加一
a[x]=true;//现在队列中有了该元素,即内存中有了该单词
}
else if(q.size()==m)//如果队列已满,即内存炸了
{
a[q.front()]=false;//将队头元素弹出之前要将该元素标为“没有在队列中出现”
q.pop();//弹出队头元素
q.push(x);//将当前元素入队
ans++;//又在外存中查询了一次词典
a[x]=true;//当前的元素标记为已出现
}
}
printf("%d",ans);//直接输出查词典的数量就结束了
return 0;
}
\(T2\)乌龟棋
题目背景:
小明过生日的时候,爸爸送给他一副乌龟棋当作礼物。
题目描述:
乌龟棋的棋盘是一行\(N\)个格子,每个格子上一个分数(非负整数)。棋盘第\(1\)格是唯一的起点,第\(N\)格是终点,游戏要求玩家控制一个乌龟棋子从起点出发走到终点。
乌龟棋中\(M\)张爬行卡片,分成\(4\)种不同的类型(\(M\)张卡片中不一定包含所有\(4\)种类型的卡片,见样例),每种类型的卡片上分别标有\(1,2,3,4\)四个数字之一,表示使用这种卡片后,乌龟棋子将向前爬行相应的格子数。游戏中,玩家每次需要从所有的爬行卡片中选择一张之前没有使用过的爬行卡片,控制乌龟棋子前进相应的格子数,每张卡片只能使用一次。
游戏中,乌龟棋子自动获得起点格子的分数,并且在后续的爬行中每到达一个格子,就得到该格子相应的分数。玩家最终游戏得分就是乌龟棋子从起点到终点过程中到过的所有格子的分数总和。
很明显,用不同的爬行卡片使用顺序会使得最终游戏的得分不同,小明想要找到一种卡片使用顺序使得最终游戏得分最多。
现在,告诉你棋盘上每个格子的分数和所有的爬行卡片,你能告诉小明,他最多能得到多少分吗?
输入输出格式:
输入格式:
每行中两个数之间用一个空格隔开。
第\(1\)行\(2\)个正整数\(N,M\),分别表示棋盘格子数和爬行卡片数。
第\(2\)行\(N\)个非负整数,\(a_1,a_2,…,a_N\),其中\(a_i\)表示棋盘第\(i\)个格子上的分数。
第\(3\)行\(M\)个整数,\(b_1,b_2,…,b_M\),表示\(M\)张爬行卡片上的数字。
输入数据保证到达终点时刚好用光\(M\)张爬行卡片。
输出格式:
\(1\)个整数,表示小明最多能得到的分数。
输入输出样例:
输入样例:
9 5
6 10 14 2 8 8 18 5 17
1 3 1 2 1
输出样例:
73
说明:
每个测试点\(1s\)
小明使用爬行卡片顺序为\(1,1,3,1,2\),得到的分数为\(6+10+14+8+18+17=73\)。注意,由于起点是\(1\),所以自动获得第\(1\)格的分数\(6\)。
对于\(30\%\)的数据有\(1≤N≤30,1≤M≤12\)。
对于\(50\%\)的数据有\(1≤N≤120,1≤M≤50\),且\(4\)种爬行卡片,每种卡片的张数不会超过\(20\)。
对于\(100\%\)的数据有\(1≤N≤350,1≤M≤120\),且\(4\)种爬行卡片,每种卡片的张数不会超过\(40\);\(0≤a_i≤100,1≤i≤N,1≤b_i≤4,1≤i≤M\)。
题解:
\(30\)分题解:
这道题我刚开始想到的是深度优先搜索(主要是最近做的搜索题太多了),但是这种方法只能得到\(30\)分,原因就是数据太毒,如果用搜索的话,复杂度应该是\(O(2^n)\)的,根本不能对其有任何奢望。但是代码还是可以看看的:
\(30\)分代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
inline int read()//读入优化
{
int F=1,num=0;
char c=getchar();
while(!isdigit(c)){if(c=='-') F=-1; c=getchar();}
while(isdigit(c)){num=num*10+c-'0'; c=getchar();}
return F*num;
}
int pos[5]={0,1,2,3,4};//这个数组存储当前出的卡片种类
int n,m;
int qi_pan[400];//棋盘上的对应得分
int ka_pian[150];//对应卡片的种类
int ans,sum;//ans是答案,sum是当前搜索的得分(将这两个值进行比较,就能得出最大值)
int num[5];//num[i]表示卡片类型为i的卡片数量
void dfs(int k,int d)//dfs(k,d)表示当前位置是k,已经用了d张卡牌
{
if(k==n)//如果当前位置已经到了终点
{
ans=max(ans,sum);//比较最大值
return ;//回溯
}
if(d==m)//如果当前已经用了所有的卡牌(因为题目保证用完所有卡牌后正好走到终点,所以这两个判断都是一样的)
{
ans=max(ans,sum);//比较最大值
return ;//回溯
}
else//如果没有到达终点
{
for(int i=1;i<=4;++i)//调用四种前进方式
{
if(num[pos[i]]>0)//如果当前前进方式仍有卡牌
{
int r=k+pos[i];//定义r为接下来搜索的起点
num[pos[i]]--;//减少一张卡牌
sum+=qi_pan[r];//已经得到的分加上当前的得分
dfs(r,d++);//继续搜索
sum-=qi_pan[r];
d--;
num[pos[i]]++;//回溯,将三个被更改过的变量进行还原
}
else//如果没有卡牌可以使用
continue;//看看下一张有没有用过(因为总会有没有用过的卡片的)
}
}
}
int main()
{
n=read(),m=read();//读入n和m
for(int i=1;i<=n;++i) qi_pan[i]=read();//读入这个棋盘
for(int i=1;i<=m;++i)
{
ka_pian[i]=read();//读入每个卡片的种类
num[ka_pian[i]]++;//处理num数组
}
dfs(1,0);//从第一个位置开始搜索,一张卡片都没有用
printf("%d",ans+qi_pan[1]);//输出时别忘了加上第一格所加的分数
return 0;//然后我们就愉快地得到30分啦!
}
\(100\)分题解:
搜索会炸,那么我们应该如何优化呢?
答案就是\(dp\)!
但是我们如何设状态呢?
接下来提供一种思路:
\(dp[a][b][c][d]\)表示第\(1\)种卡片用了\(a\)张,第\(2\)种卡片用了\(b\)张,第\(3\)种卡片用了\(c\)张,第\(4\)种卡片用了\(d\)张时的最大得分。
这样我们就可以以\(a\)(第\(1\)张卡片)为例推导一下状态转移方程:
\(if(num[a]>0)\space\space dp[a][b][c][d]=max(dp[a][b][c][d],dp[a-1][b][c][d]+qipan[now])\)
\(now=1+a+2*b+3*c+4*d\)
其余的方程大家可以自己推一下,都是一样的。
\(100\)分代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
inline int read()//一模一样的快读
{
int F=1,num=0;
char c=getchar();
while(!isdigit(c)){if(c=='-') F=-1; c=getchar();}
while(isdigit(c)){num=num*10+c-'0'; c=getchar();}
return num*F;
}
int n,m;
int qi_pan[400];//定义同上
int num[5];//定义同上
int dp[45][45][45][45];//4维dp的每一维都要在40位以上,否则就会RE
int main()
{
n=read(),m=read();
for(int i=1;i<=n;++i) qi_pan[i]=read();
for(int i=1;i<=m;++i)
{
int x=read();
num[x]++;
}
for(int i=0;i<=num[1];++i)
for(int j=0;j<=num[2];++j)
for(int k=0;k<=num[3];++k)
for(int l=0;l<=num[4];++l)
{
int now=1+1*i+2*j+3*k+4*l;//计算当前的得分
if(i) dp[i][j][k][l]=max(dp[i][j][k][l],dp[i-1][j][k][l]+qi_pan[now]);
if(j) dp[i][j][k][l]=max(dp[i][j][k][l],dp[i][j-1][k][l]+qi_pan[now]);
if(k) dp[i][j][k][l]=max(dp[i][j][k][l],dp[i][j][k-1][l]+qi_pan[now]);
if(l) dp[i][j][k][l]=max(dp[i][j][k][l],dp[i][j][k][l-1]+qi_pan[now]);//状态转移方程
}
printf("%d",dp[num[1]][num[2]][num[3]][num[4]]+qi_pan[1]);//我们要的答案就是所有卡牌都用上后的最大得分加上第一个位置对应的分数
return 0;//AC了
}
\(T4\)引水入城:
(\(T3\)关押罪犯博主暂时不会,就先咕咕咕了)
题目描述:
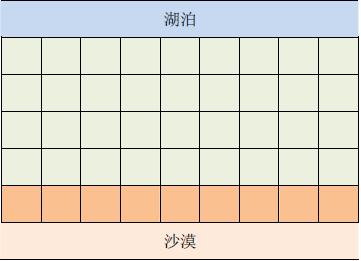
在一个遥远的国度,一侧是风景秀美的湖泊,另一侧则是漫无边际的沙漠。该国的行政区划十分特殊,刚好构成一个\(N\) 行\(\times M\) 列的矩形,如上图所示,其中每个格子都代表一座城市,每座城市都有一个海拔高度。
为了使居民们都尽可能饮用到清澈的湖水,现在要在某些城市建造水利设施。水利设施有两种,分别为蓄水厂和输水站。蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中。
因此,只有与湖泊毗邻的第\(1\)行的城市可以建造蓄水厂。而输水站的功能则是通过输水管线利用高度落差,将湖水从高处向低处输送。故一座城市能建造输水站的前提,是存在比它海拔更高且拥有公共边的相邻城市,已经建有水利设施。由于第\(N\) 行的城市靠近沙漠,是该国的干旱区,所以要求其中的每座城市都建有水利设施。那么,这个要求能否满足呢?如果能,请计算最少建造几个蓄水厂;如果不能,求干旱区中不可能建有水利设施的城市数目。
输入输出格式:
输入格式:
每行两个数,之间用一个空格隔开。输入的第一行是两个正整数\(N,M\),表示矩形的规模。接下来\(N\) 行,每行\(M\) 个正整数,依次代表每座城市的海拔高度。
输出格式:
两行。如果能满足要求,输出的第一行是整数\(1\),第二行是一个整数,代表最少建造几个蓄水厂;如果不能满足要求,输出的第一行是整数\(0\),第二行是一个整数,代表有几座干旱区中的城市不可能建有水利设施。
输入输出样例:
输入样例\(1\):
2 5
9 1 5 4 3
8 7 6 1 2
输出样例\(1\):
1
1
输入样例\(2\):
3 6
8 4 5 6 4 4
7 3 4 3 3 3
3 2 2 1 1 2
输出样例\(2\):
1
3
说明:
样例\(1\)说明:
只需要在海拔为\(9\)的那座城市中建造蓄水厂,即可满足要求。
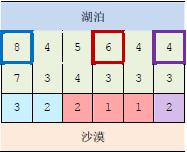
样例\(2\)说明:
上图中,在\(3\)个粗线框出的城市中建造蓄水厂,可以满足要求。以这\(3\)个蓄水厂为源头在干旱区中建造的输水站分别用\(3\) 种颜色标出。当然,建造方法可能不唯一。
数据范围:
题解:
刚拿到题时,本人表示一脸懵逼。我$@%@#%@#@#,这@%@#%&什么!@#@^!题啊???
解决方法当然是问大佬啊!\(\Omega\omega\Omega\)
首先我们考虑一个问题:
如果将湖边的某一个城市作为蓄水厂,那么这个城市所对应的下游沙漠边缘的城市一定是一条连续的序列
怎么证明呢???
反证法:(摘自洛谷中某位大佬的题解)
假设存在一种情况使得覆盖情况如下, 覆盖不连续:
假设蓝色覆盖路线如下:
因为右边红色被覆盖了, 所以从红色水库到下方必然有一条路径
发现路径必有交(紫色部分), 所以红色水库的水也会流入蓝色那部分, 假设不成立
这样的话,我们可以跑一个搜索,处理出第一行每一个城市所对应的最后一行区间左右端点。然后跑一边贪心,处理区间覆盖问题就可以了
代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
inline int read()//又是这个快读
{
int F=1,num=0;
char c=getchar();
while(!isdigit(c)){if(c=='-') F=-1; c=getchar();}
while(isdigit(c)){num=num*10+c-'0'; c=getchar();}
return num*F;
}
int dx[5]={0,1,0,-1,0},dy[5]={0,0,1,0,-1};//存储搜索时的4个方向
int l[550][550],r[550][550];//l[x][y]和r[x][y]存储对应坐标(x,y)向下的左右区间端点
bool vis[550][550];//判断坐标是否被访问过
int map[550][550];//存图
int n,m;
void dfs(int x,int y)//搜索点(x,y)
{
vis[x][y]=true;//先标记为搜过
for(int i=1;i<=4;++i)//四个方向
{
int nx=x+dx[i],ny=y+dy[i];
if(nx<1||ny<1||nx>n||ny>m) continue;//如果出界了,就继续下一个方向
if(map[nx][ny]>=map[x][y]) continue;//如果不能流下,就继续下一个方向
if(!vis[nx][ny]) dfs(nx,ny);//如果当前点没有被搜索过,就搜索
l[x][y]=min(l[x][y],l[nx][ny]);//当前点的左端点为该点与下一个点的左端点的最小值(最靠左)
r[x][y]=max(r[x][y],r[nx][ny]);//当前点的右端点为该点与下一个点的右端点的最大值(最靠右)
}//其实这是一个递归过程,程序先找到最深的一层,然后用这一层的数值来更新前面几层的数值
}
int main()
{
n=read(),m=read();
memset(l,0x3f,sizeof(l));//清空l数组
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
map[i][j]=read();
for(int i=1;i<=m;++i) l[n][i]=r[n][i]=i;//初始化,令最后一排的每个城市的左端点和右端点都为自己
for(int i=1;i<=m;++i) if(!vis[1][i]) dfs(1,i);//如果第一行的某城市还没有被搜索过,就搜索这个城市
int how=0;//how是用来记录解的个数的
for(int i=1;i<=m;++i) if(!vis[n][i]) ++how;//从左往右扫一遍,如果有没有访问过的点,how+1
if(how!=0)//如果有未访问过的点
{
printf("0\n%d",how);//输出未访问过的点的个数,即没有水的城市的个数
return 0;//直接结束程序
}
int lft=1;//这个是用来存储当前的左端点的
while(lft<=m)//如果没有完全覆盖
{
int maxn=0;//其实是代表了右端点的最值
for(int i=1;i<=m;++i) if(l[1][i]<=lft) maxn=max(maxn,r[1][i]);//扫描一遍第一排的左端点,并且进行比较,来更新maxn的值,区间覆盖问题的思路
how++;//每选一个就将答案加一
lft=maxn+1;//然后找下一个区间
}
printf("1\n%d",how);//输出
return 0;
}