图论练习题——医院设置

目录：

·题目描述

·题目分析

·思路分析

·代码实现

·总结

---

 

·题目描述：

　　（洛谷P1364 医院设置）

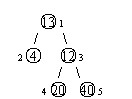
　　设有一棵二叉树，如图：

　　

 

　　其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为1。如上图中，

　　若医院建在1 处，则距离和=4+12+2*20+2*40=136；若医院建在3 处，则距离和=4*2+13+20+40=81

·题目分析：

　　这道题是图论算法中的Floyd算法（因为数据太水），下面简单介绍一下Floyd算法：

　　在一个无向图上，求任意两点的最短距离，可以使用Floyd算法。算法的大体框架是这样的：　　

　　如果i,j两点之间存在一点k，使得g[i][k]+g[k][j]<g[i][j],此时更新最小值，g[i][j]=g[i][k]+g[k][j]。并且在写代码时，必须将k放在最外层。 否则会导致g[i][j]过早的被确定下来。

·思路分析：

　　对于这道题，可以先跑一遍Floyd，然后枚举每一个结点，求出最小值

·代码实现：

#include<iostream>

using namespace std;

int a[101];
int g[101][101];//g[i][j]表示第i点到第j点的最短距离 

int main()
{
    int n,i,j,k,l,r,min,total;
    //freopen("hospital.in","r",stdin);
    //freopen("hospital.out","w",stdout);
    cin>>n;
    for(i=1;i<=n;i++)//注意初始化
    {
        for(j=1;j<=n;j++)
        {
            g[i][j]=1000000;
        }
    }
    for(i=1;i<=n;i++)//读入数据，初始化 
    {
        g[i][i]=0;
        cin>>a[i]>>l>>r;
        if(l>0) g[i][l]=g[l][i]=1;
        if(r>0) g[i][r]=g[r][i]=1;    
    }
    for(k=1;k<=n;k++)//floyd算法，求任意两点间的最短距离 
    {
        for(i=1;i<=n;i++)
        {
            if(i!=k)
            {
                for(j=1;j<=n;j++)
                {
                    if(i!=j&&k!=j&&g[i][k]+g[k][j]<g[i][j])
                        g[i][j]=g[i][k]+g[k][j];
                }
            }
        }
    }
    min=0x7fffffff;
    for(i=1;i<=n;i++)//穷举医院建在n个节点，找出最短距离。 
    {
        total=0;//一定要记得清零 
        for(j=1;j<=n;j++)
        {
            total+=g[i][j]*a[j];
        }
        if(total<min) min=total;
    }
    cout<<min<<endl;
    return 0; 
}

·总结：

　　Floyd算法是图论算法中最基础的算法（没有之一），一定要牢记。因为在关键时刻还是可以骗点分的QwQ