高级算法--贪心

下面是对信息学奥赛一本通网站评测上的AC代码的总结

·例一：

题目描述：

　　设有n个活动的集合E={1,2,…,n}，其中每个活动都要求使用同一资源，如演讲会场等，而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间si和一个结束时间fi,且si <fi。如果选择了活动i，则它在半开时间区间[si, fi)内占用资源。若区间[si, fi)与区间[sj, fj)不相交,则称活动i与活动j是相容的。也就是说，当si≥fj或sj≥fi时，活动i与活动j相容。选择出由相互兼容的活动组成的最大集合。

代码实现：

 

#include<algorithm>
#include<iostream>
#include<cstdio>

using namespace std;

struct node
{
    int st;
    int ed;
}a[1005];

bool cmp(node x,node y)
{
    return x.ed<y.ed;
}

int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;++i)    scanf("%d%d",&a[i].st,&a[i].ed);
    sort(a+1,a+n+1,cmp);
    int t=a[1].ed;
    int ans=1;
    for(int i=2;i<=n;++i)
    {
        if(a[i].st>=t)
        {
            ans++;
            t=a[i].ed;
        }
    }
    printf("%d",ans);
    return 0;
}

 

·例二：

题目描述：

　　现在我们国家开展新农村建设，农村的住房建设纳入了统一规划，统一建设，政府要求每一住户门口种些树。门口路边的地区被分割成块，并被编号成1..N。每个部分为一个单位尺寸大小并最多可种一棵树。每个居民房子门前被指定了三个号码B，E，T。这三个数表示该居民想在B和E之间最少种T棵树。当然，B≤E，居民必须记住在指定区不能种多于区域地块数的树，所以T≤E-B+l。居民们想种树的各自区域可以交叉。你的任务是求出能满足所有要求的最少的树的数量，尽量较少政府的支出。

代码实现：

#include<iostream>
#include<cstdio>
#include<algorithm>

using namespace std;

struct line{int s,e,v;}a[5005];

int n,m;

bool used[30005]={0};

bool cmp(const line &x,const line &y){return x.e<y.e;}

void init()
{
    int i;
    scanf("%d%d",&n,&m);
    for(i=1;i<=m;++i) scanf("%d%d%d",&a[i].s,&a[i].e,&a[i].v);
    sort(a+1,a+m+1,cmp);
}

void solve()
{
    int i,j,k,ans=0;
    for(int i=1;i<=m;++i)
    {
        k=0;
        for(j=a[i].s;j<=a[i].e;++j)    if(used[j]) ++k;
        if(k>=a[i].v) continue;
        for(j=a[i].e;j>=a[i].s;--j)
            if(!used[j])
            {
                used[j]=1;
                k++;
                ans++;
                if(a[i].v==k) break;
            }
    }
    printf("%d",ans);
}

int main()
{
    init();
    solve();
    return 0;
}

·例三：

题目描述：

长L米，宽W米的草坪里装有n个浇灌喷头。每个喷头都装在草坪中心线上（离两边各W/2米）。我们知道每个喷头的位置（离草坪中心线左端的距离），以及它能覆盖到的浇灌范围。

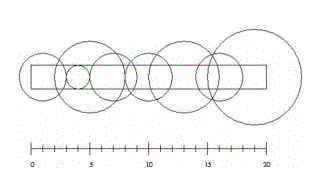
请问：如果要同时浇灌整块草坪，最少需要打开多少个喷头？

代码实现：

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#define N 300005
 
using namespace std;
 
const double Eps = 1e-5 ;
 
inline int wread(){
    char c=getchar ();int flag=1,wans=0;
    while (c<'0'||c>'9'){if (c=='-') flag=-1;c=getchar ();}
    while (c>='0'&&c<='9'){wans=wans*10+c-'0';c=getchar ();}
    return wans*=flag;
}
 
int T;
int n,L,W;
struct node {double lx,rx;int pos,r;}a[N];
bool e666 (node x,node y){return x.lx<y.lx;}
 
int main (){
    T=wread();
    while (T--){
        memset (a,0,sizeof a);
        n=wread();L=wread();W=wread();
        for (int i=1;i<=n;++i){
            a[i].pos=wread(),a[i].r=wread();
            if (a[i].r*a[i].r-(W*1.0/2.0)*(W*1.0/2.0)<0)    a[i].pos=-1,a[i].lx=-1,a[i].rx=-1;
            //对于不能覆盖完草坪上端的一个圆(例如样例1中的那个夹在草坪中间的圆) 肯定是不会选它的 
            else {
                a[i].lx=max (0.000000,(double)a[i].pos-sqrt((double)a[i].r*(double)a[i].r-(W*1.0/2.0)*(W*1.0/2.0)));
                a[i].rx=a[i].pos+sqrt((double)a[i].r*(double)a[i].r-(W*1.0/2.0)*(W*1.0/2.0));                    
            }
        }
 
        sort (a+1,a+n+1,e666);    
        
        int nx=1; 
        double s=0;//起点 
        bool F=true;//判断是否能覆盖完整个区间 
        int ans=0;//记录 
        
        while (nx<=n){
            ans++;
            double re=s;
            while (a[nx].lx<=re && nx<=n){//模板 
                if (a[nx].rx>=re)    s=max(s,a[nx].rx);
                nx++;
            }
            if (s>=L)    {break;}
            if (re==s)    {F=false;break;}//未更新,请画图____即当前区间与下个区间之间 一定有一段距离,不符合全部覆盖的要求,退出 
        }
        if (!F)    puts("0");
        else    printf("%d\n",ans);
    }
    return 0;
}

·例四：

题目描述：

　　某工厂收到了n个产品的订单，这n个产品分别在 A、B 两个车间加工，并且必须先在 A 车间加工后才可以到 B 车间加工。

某个产品i在 A，B 两车间加工的时间分别为Ai，Bi。怎样安排这个产品的加工顺序，才能使总的加工时间最短。

这里所说的加工时间是指：从开始加工第一个产品到最后所有的产品都已在 A，B 两车间加工完毕的时间。

代码实现：

#include<cstdio>
#include<iostream>

using namespace std;

int ans[1005],n,k,i,j,t,a[1005];
int b[1005],m[1005],s[1005];

void read()
{
    int i;
    scanf("%d",&n);
    for(i=1;i<=n;++i) scanf("%d",&a[i]);
    for(i=1;i<=n;++i) scanf("%d",&b[i]);
}

void solve()
{
    for(i=1;i<=n;++i){m[i]=min(a[i],b[i]);s[i]=i;}
    for(i=1;i<=n-1;++i)
        for(j=i+1;j<=n;++j)
            if(m[i]>m[j]){swap(m[i],m[j]);swap(s[i],s[j]);}
    k=0;t=n+1;
    for(i=1;i<=n;++i)
        if(m[i]==a[s[i]]){k++;ans[k]=s[i];}
        else{t--;ans[t]=s[i];}
    k=0;t=0;
    for(i=1;i<=n;++i)
    {
        k+=a[ans[i]];
        if(t<k) t=k;
        t+=b[ans[i]];
    }
    printf("%d\n",t);
    for(i=1;i<=n;++i) printf("%d ",ans[i]);
    printf("\n");
}

int main()
{
    read();
    solve();
    return 0;
}