清北学堂学习总结day3

小学知识总结

上午篇

•积性函数的卷积公式

　　（1）（f * g）( n ) = ∑(d|n) f( d ) x g ( n / d )

　　（2）代码实现

    LL f[N], g[N], h[N];
   void calc(int n) {
   for (int i = 1; i * i <= n; i++) {
   h[i * i] += f[i] * g[i];
   for (int j = i + 1; i * j <= n; j++)
   h[i * j] += f[i] * g[j] + f[j] * g[i];
   }
   } 

　　（3）例题

　　　　太难了就不发了QAQ

•组合数问题都是好题 / / 钟神的小学题

　　（1）加法原理和乘法原理

　　（2）加法原理：具有性质A的事件有m个，具有性质B的事件有n个，则具有性质A 或 性质B的事件有m+n个

　　（3）乘法原理：具有性质A的事件有m个，具有性质B的事件有n个，则具有性质A 及 性质B的事件有mn个

　　（4）例题：

　　　　　　•1、求小于10000的正整数中含有数字1的个数   （计数问题）

　　　　　　　　介是红题呀！！！   可是好像要手推QAQ

　　　　　　　　可以一位一位的看，分别讨论各位上含有数字1的个数，然后用加法原理，相加可得结果，具体过程就                          不写了，这里只提供思路

　　　　　　•2、n = 7³ * 11² * 13⁴，求n的因子个数

　　　　　　　　好像很水，可以用乘法原理，3 * 4 * 5 = ？？？ （数据太大，脑子不够用）

　　　　　　•3、书店有【日文书】* 5、【英文书】* 7、【中文书】* 10，问：取两册文字不同的书有多少种方案？取两                               册文字相同的书有多少种方案？随便取两册有多少种方案？

　　　　　　　　这道题留作思考题吧，比较综合（其实是懒得打了）

　　（5）排列组合

　　　　　　•1、这其实是两个不同的东西（说了句废话

　　　　　　•2、组合:（其实应该先讲排列

　　　　　　　　从n个数中选取r个元素，当不计顺序时，其方案数为：

　　　　　　　　

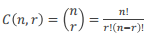
　　　　　　•3、排列：（其实应该用A

　　　　　　　　从n个元素中选取r个元素，当考虑顺序时，其方案数为：

　　　　　　　　

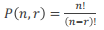
　　（6）例题：（当做练习题，有疑惑自己百度

　　　　　　•1、有5面颜色不同的旗帜，20种不同的盆花，排成两端是两面旗帜，中间是三盆花的形式，问有多少方案数？

　　　　　　•2、7男3女排队，要求头尾必须是男，且女不相邻，求方案数？

　　　　　　•3、求2000-7000的偶数中，由不同的数字组成的四位数的个数？

　　　　　　•4、5女7男选5个组成战队中路组团送，但是男A和女B不能同时选，问方案数？

　　　　　　•5、从1-300选3个数，使得它们的和能被3除尽，问方案数？

　　　　　　•6、红黄蓝绿旗帜各四面排成一列，问方案数？

　　　　　　•7、有n个不同元素，从中选r个，但是每个可以选多次（可重），求证：其方案数为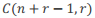

　　　　　　•8、有n个不同元素，从中选r个，但是选择的元素不能相邻，求证：其方案数为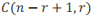

　　（7）组合数及其相关性质 ( 直接上图吧

　　　　　　

下午篇

　　（1）容斥原理

　　　　　　

　　　　　　可以结合韦恩图来表示

　　（2）例题：

　　　　　　•选修数学、物理、化学的各有170、130、120人，选修数学和物理有45人，选修数学和化学有20人， 选修物理和化学有22人，三修有3人，问总共有多少人？

 　　　　　　

 

PS：剩下的题就不发了，只是发了一些蒟有代表性的题（比较简单），难度较大的题就压根没整理