dp的优化[1]

本文将会简单介绍一下优化：

1. 改变状态的定义
2. 套用其他算法或数据结构
3. 斜率

problem 1

最长上升子序列，原序列$a$的长度为$n$，$n\le 10^5$。

idea 1 数据结构

最原始的做法，$f(i)$表示用第$i$做结尾的最长上升子序列。那么$f(i)=\underset{j<i,a_j<a_i}{\max }\{f(j)+1\}$。原始时间复杂度是$O(n^2)$。性能的瓶颈在转移时的枚举，每次的枚举都要查找$i$之前的所有位置，但是有用的却只有那些值小于$a_i$的那些。

因此需要一种数据结构，能够快速单点修改，快速查找前缀最大值，比如线段树。

每次转移查找该数据结构中$[1,a_i)$的最大值，得到$f(i)$之后将它加入到$a_i$所在的位置中，如果$a_i$的范围是整型范围的话，就需要使用离散化。

$dp$总体时间复杂度$O(n{\log }_{2}n)$

idea 2 改变状态

我们知道，如果子序列中第$i$个元素越小，那么后面可以容纳的元素应该会更多。

用$f(i,l)$表示考虑到原序列的第$i$个元素，子序列的长度为$l$的最后一个元素的最小值是多少，那么

$f(i,l)=\max \{\begin{array}{ll}{a}_i& f(i-1,l-1)<a_i<f(i-1,l-1)\\ f(i-1,l)& otherwise\end{array}$

在加维的路上越走越远

看起来复杂度似乎没什么变化，但是对于每一个$i$,从$1$到$l$的$f(i,\ast )$是单调不下降的（原因感性理解），所以每个i每次只能更新一个$l$。其他的是拷贝$i-1$的内容的，故此，我们，我们将第一维缩去，二分得到每个$a_i$可以到达的位置，然后更新数组。

int ans = 0;
f[0] = -INF;
for (int i = 1; i <= n; i++) {
    if (a[i] > f[ans]) f[++ans] = a[i];
    else {
        int pos = find(a[i]);
        f[pos] = a[i];
    }
}

problem 2

有$0$到$n$+1 共$n+2(n\le 10^7)$个位置，每个位置都有一个分数$a_i$，特别的，$a_0=a_{n+1}=0$，现在从0号位置出发，每次可以前进步数$c$，满足$s\le c\le t$,问到达$n+1$后得到的最大分数和.

idea 数据结构

按照原始思路,$f(i)$表示到达位置$i$后得到的最大分数和.那么

$f(i)=\underset{s\le j\le t,0\le i-j}{\max }\{f(i-j)\}+a_i$

这样显然会$TLE$,但是这是一个区间求最大值问题，可以使用线段树什么的，但由于$n$比较大，${\log }_{2}n$的数据结构依然会$TLE$，于是我们需要更快速的数据结构——单调队列，不是优先队列,这个队列实际上是一个栈还有队列的结合体，前段队列，后段栈，$STL$中叫$deque$。

先看看小例题

有一个序列$a$，长度$n$，要求计算出所有的$a[i,i+l-1]$的最大值。

simple：$a=\{1,6,3,4,8,7\}$, $l=3$

1. 首先加入第一个数1，同时记录他的位置,得到队列$\{(v:1,p:1)\}$

2. 接着加入第二个数6,发现队列中最后一个元素(目前也是第一个):$1$，比6要小，可以得知元素$1$已经没用了，因为后来的6比它要大，若两个都在查询区间中，答案肯定不会是1，而且1所在位置在6之前，往后的查询中不可能只出现1而不出现6。形象点来说：比你小（位置靠后），还比你强（值比你大），你就永远打不过他（不可能作为查询结果），那么得到队列$\{(v:6,p:2)\}$

3. 接着加入元素$3$，这个又怎么办呢，首先，如果这两个都在查询区间内，那么肯定是6作为答案，但是有可能有3在查询区间中，目前我们并不知道后面的书会怎样，所以3可能作为答案，所以3需要保留，得到队列$\{(v:6,p:2),(v:3,p:3)\}$

   这样的话，[1,3]的答案就是6了；

4. 接着到第4个元素4,遵循粗体字，我们将3舍去，得到队列$\{(v:6,p:2),(v:4,p:4)\}$

   得到答案6

5. 接着，我们发现，第一个元素的位置已经在之后的查询区间以外了，不可能作为答案，于是将第一个元素舍去（在实际问题中，可能一次要舍去多个元素）$\{(v:4,p:4)\}$

   接着得到元素8,于是序列如下$\{(v:8,p:5)\}$

   得到答案8

6. 得到元素7,序列如下$\{(v:8,p:5),(v:7,p:6)\}$

   得到答案8

7. 没有元素可以加入
   得到答案8

8. 队头元素不合法，去除序列如下$\{(v:7,p:6)\}$

   得到答案7

继续

那么原问题就可以用单调队列完成了，代码本人不想写（本人码风很差）

由于单调队列中的每个元素只会进出一次，所以总的时间复杂度为$O(n)$

problem 3

$N$个任务排成一个序列在一台机器上等待完成（顺序不得改变），这$N$个任务被分成若干批，每批包含相邻的若干任务。从时刻0开始，这些任务被分批加工，第$i$个任务单独完成所需的时间是$T_i$。在每批任务开始前，机器需要启动时间$S$，而完成这批任务所需的时间是各个任务需要时间的总和（同一批任务将在同一时刻完成）。每个任务的费用是它的完成时刻乘以一个费用系数$F_i$。请确定一个分组方案，使得总费用最小。

例如：$S=1$；$T=\{1,3,4,2,1\}$；$F=\{3,2,3,3,4\}$。如果分组方案是$\{1,2\}$、$\{3\}$、$\{4,5\}$，则完成时间分别为$\{5,5,10,14,14\}$，费用$C=\{15,10,30,42,56\}$，总费用就是$153$。

$\forall T_i,C_i>0$,$n\le 3\times 10^5$

idea 1

求出$T,C$的前缀和$sT,sC$，用$f(i,j)$表示前$i$个任务分成$j$批所需要的最小费用，那么:

$f(i,j)=\underset{0\le k<i}{\min }\{f(k,j-1)+(S\times j+s{T}_i)+(s{C}_i-s{C}_k)\}$

这样的话就是复杂度就是$O(n^3)$

idea 2

我们并不需要知道任务被分成了多少批，因为将这批任务对之后的任务的完成时间的影响都加起来，用$f(i)$表示前$i$个任务分成若干批后的最小费用，那么:$f(i)=\underset{0\le j<i}{\min }\{f(j)+s{T}_i\times (s{C}_i-s{C}_j)+S\times (s{C}_N-s{C}_j)\}$ 这样的话，就可以做到$O(n^2)$了，但是我们依然不能解决这个问题，

我们对转移方程做一下变化，将常数，和$i$有关，和$j$有关,和$i,j$有关的项分开：$f(i)=\underset{0\le j<i}{\min }\{f(j)-s{C}_j\times (s{T}_i+S)\}+s{T}_i\times s{C}_i+S\times s{C}_N$

然后将min去掉，得到$f(i)=f(j)-s{C}_j\times (s{T}_i+S)+s{T}_i\times s{C}_i+S\times s{C}_N$

设$y=f(j),k=s{T}_i+S,x=s{C}_j,C=s{T}_i\times s{C}_i+S\times s{C}_N$

那么上面的式子就可以表示成这个样子 : $f(i)=y-kx+C$。

然后移项:$y=kx+f(i)-C$

这个就很像在以$s{C}_j$为$x$轴，以$f(j)$为$y$轴的平面直角坐标系中的一次函数表达式了,而我们要让$f(i)$最小，那么就等价与让截距最小

来一个example。

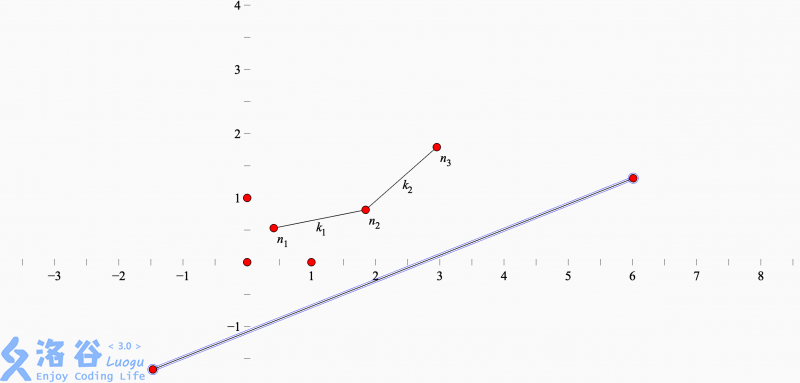
我们看看有什么情况下必然会取到某个点作为最优值。

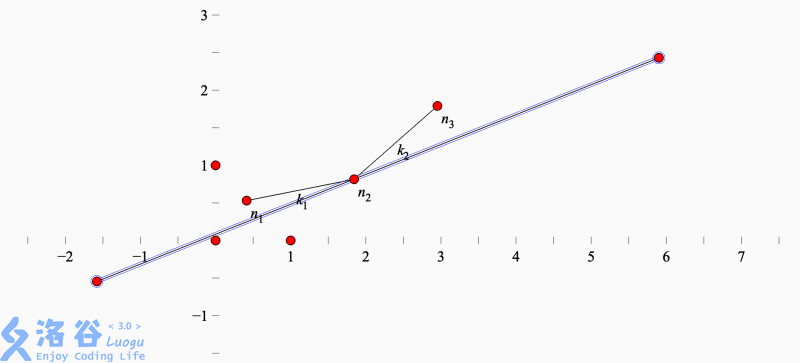
对于类似这样情况，最优值应该是和$n_2$有关的，而与他相关的斜率$k_1,k_2$以及$k$满足$k_1<k<k_2$

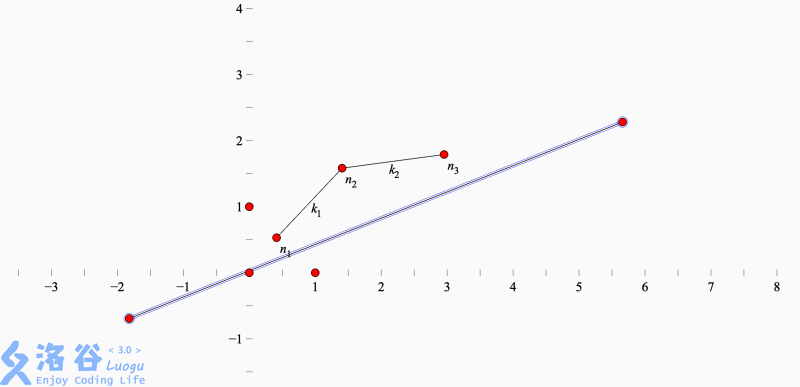
对于这种情况，最优值不会和$n_2$有关系，而此时$k_1>k_2$

所以，有可能贡献答案的点组成的序列$n_i$必须要满足$k_{i-1}<k_i$，在原题中就是$\frac{f(n_i)-f(n_{i-1})}{s{C}_{n_i}-s{C}_{n_{i-1}}}<\frac{f(n_{i+1})-f(n_i)}{s{C}_{n_{i+1}}-s{C}_{n_i}}$，而最优值的位置会把序列分成两半（长度可能不等），接着因为$s{C}_i$单调递增，所以新的点出现的位置应该是之前所有的点的右边，又因为$\forall T_i>0$，所以$s{T}_i$单调递增，所以求出的$k=S+s{T}_i$也是单调递增的，所找到的最优值的位置只可能越来越靠后，所以可以判定，分成两半的序列中，前半部分已经没用了，而最优值的位置应该是在后半部分的第一个。

于是我们用单调队列，每次转移时先去除斜率比$k=S+s{T}_i$小的元素，然后找到队首计算最优值，接着插入第$i$个元素。

code

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>

using namespace std;

const int maxn = 5e3 + 5;
int C[maxn], T[maxn], S, N;
int f[maxn], q[maxn], l = 1, r = 1;

void pop(int i) {
    while (l < r
        && f[q[l + 1]] - f[q[l]] < (S + T[i]) * (C[q[l + 1]] - C[q[l]]))
        l++;
}
void push(int i) {
    while (l < r
        && (f[q[r]] - f[q[r - 1]]) * (C[i] - C[q[r]]) >= (f[i] - f[q[r]]) * (C[q[r]] - C[q[r - 1]]))
        r--;
    q[++r] = i;
}

int main() {
    // freopen("testdata.in", "r", stdin);
    // freopen("testdata.out", "w", stdout);
    scanf("%d%d", &N, &S);
    for (int i = 1; i <= N; i++)
        scanf("%d%d", &T[i], &C[i]), 
        T[i] += T[i - 1], C[i] += C[i - 1];
    memset(f, 0x3f, sizeof(f));
    f[0] = q[1] = 0;
    for (int i = 1; i <= N; i++) {
        pop(i);
        f[i] = f[q[l]] - (S + T[i]) * C[q[l]] + T[i] * C[i] + S * C[N];
        push(i);
    }
    printf("%d\n", f[N]);
    return 0;
}