[整理]CSP-S 2023 题解

题简单还考稀烂，别学了。

T1 密码锁

观察数据范围，可以直接枚举密码。

#include<bits/stdc++.h>
#define ls (k<<1)
#define rs (k<<1|1)
#define nmid ((l+r)>>1)
#define tmid ((tr[k].l+tr[k].r)>>1)
#define x first
#define y second
#define INF 0x3f3f3f3f
#define rep(i, l, r) for(int (i)=(l); (i)<=(r); i++)
#define per(i, r, l) for(int (i)=(r); (i)>=(l); i--)
using namespace std;
inline void Read(int &x){
  char c=getchar(); int f=1;
  x=0;
  while(c<'0' or c>'9'){
    if(c=='-') f=-1;
    c=getchar();
  }
  while(c>='0' and c<='9'){
    x=(x<<3)+(x<<1)+c-'0';
    c=getchar();
  }
  x*=f;
}
int n;
int p[10], a[20][10];
int main(){
  Read(n);
  rep(i, 1, n) rep(j, 1, 5) Read(a[i][j]);
  int ans=0;
  rep(o, 0, 99999){
    p[1]=o%10, p[2]=o/10%10, p[3]=o/100%10;
    p[4]=o/1000%10, p[5]=o/10000%10;
    bool ff=1;
    rep(i, 1, n){
      int lst=-1, cnt=0, d=114514;
      rep(j, 1, 5){
        if(p[j]!=a[i][j]){
          if(lst==-1 and cnt==0){
            lst=j, cnt++, d=(a[i][j]-p[j]+10)%10;
          }else {
            if(lst!=j-1 or cnt>1){
              ff=0; break;
            }else {
              if((a[i][j]-p[j]+10)%10!=d){
                ff=0; break;
              }
              lst=i, cnt++;
            }
          }
        }
      }
      if(cnt==0) ff=0;
    }
    if(ff) ans++;
  }
  printf("%d\n", ans);
  return 0;
}

T2 消消乐

观察数据范围，我们需要一个 \(O(n\log n)\) 或 \(O(n)\) 的算法。首先考虑 DP，设 \(f_i\) 表示 \([1, i]\) 中有多少合法串，发现转移时会有重复，如 abbaabba。想想常见的去重手段，可以钦定从后往前依次消最短的，这样 abbaabba 就只会用两次 abba 消去。

然后考虑复杂度，我们需要快速求出以每个位置为右端点的最短合法串，记他的左端点为 \(\text{last}_i\)。这时考虑 \(\text{last}\) 的性质，我们顺着 \(\text{last}_{i-1}\) 往前跳，如果跳到和 \(s_i\) 相同的，就说明找到了一个合法串。如图所示：

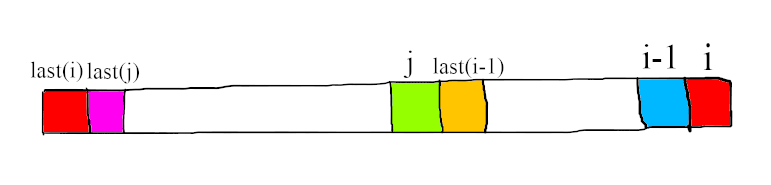
这样做的复杂度是多少呢？看似是 \(O(n^2)\) 的，实际上能过。据说实际是 \(O(|\Sigma|n)\) 的，证明后补。

#include<bits/stdc++.h>
#define eps 1e-10
#define INF 0x3f3f3f3f
#define rep(i, l, r) for(int i=(l); i<=(r); i++)
#define per(i, r, l) for(int i=(r); i>=(l); i--)
#define ls k<<1
#define rs k<<1|1
#define tmid ((tr[k].l+tr[k].r)>>1)
#define nmid ((l+r)>>1)
#define pub push_back
#define all(v) v.begin(), v.end()
#define pii pair<int, int>
#define mkp make_pair
#define x first
#define y second
using namespace std;
#define int long long
inline void Read(int &x){
  int f=1; x=0;
  char c=getchar();
  while(c<'0' || c>'9'){
    if(c=='-') f=-1;
    c=getchar();
  }
  while(c>='0' && c<='9'){
    x=(x<<3)+(x<<1)+c-'0', c=getchar();
  }
  x*=f;
}
const int N=2e6+10;
int n; char s[N];
// f[i]: good substrs ending with i
// lst[i]: [lst[i], i] is a minimum good substr
int f[N], lst[N];
signed main(){
  Read(n), scanf("%s", s+1);
  lst[1]=0, lst[2]=(s[1]==s[2]);
  rep(i, 3, n){
    int j=i-1;
    while(j>0 and s[j]!=s[i]){
      j=lst[j]-1;
    }
    if(j==-1) lst[i]=0;
    else lst[i]=j;
  }
  rep(i, 1, n){
    if(lst[i]>0) f[i]=f[lst[i]-1]+1;
  }
  int ans=0;
  rep(i, 1, n) ans+=f[i];
  printf("%lld\n", ans);
  return 0; 
}

T3 结构体

大模拟，由于数据小，直接写就能过。一定要贯彻简化、合并的思想，才不会写乱。另外，也需要注意信息存够，例如成员重名问题，可以通过多存一下所在结构体解决。

#include<bits/stdc++.h>
#define ls (k<<1)
#define rs (k<<1|1)
#define nmid ((l+r)>>1)
#define tmid ((tr[k].l+tr[k].r)>>1)
#define x first
#define y second
#define mkp make_pair
#define pub push_back
#define pss pair<string, string>
#define INF 0x3f3f3f3f
#define rep(i, l, r) for(int (i)=(l); (i)<=(r); i++)
#define per(i, r, l) for(int (i)=(r); (i)>=(l); i--)
using namespace std;
#define int long long
inline void Read(int &x){
  char c=getchar(); int f=1;
  x=0;
  while(c<'0' or c>'9'){
    if(c=='-') f=-1;
    c=getchar();
  }
  while(c>='0' and c<='9'){
    x=(x<<3)+(x<<1)+c-'0';
    c=getchar();
  }
  x*=f;
}
const int N=10010;
int n;
map<pss, string> typ;// type
map<string, int> siz, req;// size, requirement
map<string, vector<pair<pss, int> > > mem;// members
vector<pair<pss, int> > p;// memory pool
// query the address of lst.tar, lst is start from st
int Query(string lst, int st, string tar){
//  cout<<"Query: "<<lst<<" "<<st<<" "<<tar<<endl;
  int pos=-1;
  rep(i, 0, (int)tar.size()-1) if(tar[i]=='.'){
    pos=i; break;
  }
  if(pos==-1){
    int sft=-1;
    for(auto o: mem[lst]){
      if(o.x.y==tar){
        sft=o.y; break;
      }
    }
    return st+sft;
  }else {
    // seek for lst.newlst.newtar
    string newlst="", newtar="";
    rep(i, 0, pos-1) newlst+=tar[i];
    rep(i, pos+1, (int)tar.size()-1) newtar+=tar[i];
    int sft=-1;
    for(auto o: mem[lst]){
      if(o.x.y==newlst){
        sft=o.y; break;
      }
    }
    return Query(typ[mkp(lst, newlst)], st+sft, newtar);
  }
}
string QueryAddress(pair<pss, int> now, int addr){
  string tp=now.x.x, nm=now.x.y;
  int st=now.y;
  if(tp=="byte" or tp=="short" or tp=="int" or tp=="long"){
    return nm;
  }
  pair<pss, int> newnow; bool ff=0;
  for(auto o: mem[tp]){
    if(st+o.y<=addr and addr<=st+o.y+siz[o.x.x]-1){
      newnow=mkp(o.x, st+o.y), ff=1; break;
    }
  }
  if(!ff) return "ERR";
  string res=QueryAddress(newnow, addr);
  if(res=="ERR") return "ERR";
  return nm+"."+res;
}
signed main(){
  ios::sync_with_stdio(false);
  cin>>n;
  siz["byte"]=1, siz["short"]=2, siz["int"]=4, siz["long"]=8;
  req["byte"]=1, req["short"]=2, req["int"]=4, req["long"]=8;
  while(n--){
    int opt; cin>>opt;
    if(opt==1){
      string nm; int k; cin>>nm>>k;
      vector<pss > tmp; int mxreq=0;
      while(k--){
        string ti, ni;
        cin>>ti>>ni, tmp.pub(mkp(ti, ni)), typ[mkp(nm, ni)]=ti;
        mxreq=max(mxreq, req[ti]);
      }
      req[nm]=mxreq;
      // get size
      int lst=0;
      rep(idx, 0, (int)tmp.size()-1){
        pss o=tmp[idx];
        if(idx==0) lst=0;
        else {
          int newsiz=lst+siz[tmp[idx-1].x], len=req[o.x];
          lst=(newsiz+len-1)/len*len;
        }
        mem[nm].pub(mkp(o, lst));
      }
      int newsiz=lst+siz[tmp.back().x], len=mxreq;
      siz[nm]=(newsiz+len-1)/len*len;
      cout<<siz[nm]<<" "<<req[nm]<<endl;
    }else if(opt==2){
      //type / name
      string tp, nm; cin>>tp>>nm, typ[mkp("", nm)]=tp;
      if(p.empty()) p.pub(mkp(mkp(tp, nm), 0));
      else {
        int newsiz=p.back().y+siz[p.back().x.x], len=req[tp];
        newsiz=(newsiz+len-1)/len*len;
        p.pub(mkp(mkp(tp, nm), newsiz));
      }
      cout<<p.back().y<<endl;
    }else if(opt==3){
      string tar; cin>>tar;
      string lst="", newtar="";
      int pos=-1;
      rep(i, 0, (int)tar.size()-1) if(tar[i]=='.'){
        pos=i; break;
      }
      if(pos==-1){
        int st=0;
        for(auto o: p){
          if(o.x.y==tar){
            st=o.y; break;
          }
        }
        cout<<st<<endl;
        continue;
      }
      rep(i, 0, pos-1) lst+=tar[i];
      rep(i, pos+1, (int)tar.size()-1) newtar+=tar[i];
      int st=0;
      for(auto o: p){
        if(o.x.y==lst){
          st=o.y; break;
        }
      }
      cout<<Query(typ[mkp("", lst)], st, newtar)<<endl;
    }else {
      int addr; cin>>addr;
      pair<pss, int> now; bool ff=0;
      for(auto o: p){
        if(o.y<=addr and addr<=o.y+siz[o.x.x]-1){
          now=o, ff=1; break;
        }
      }
      if(!ff){
        cout<<"ERR"<<endl; continue;
      }
      cout<<QueryAddress(now, addr)<<endl;
    }
  }
  return 0;
}

T4 种树

首先看最短时间不好求，想到二分答案，转为判断某个时间是否可行。

然后由于树的种下时间不知道，我们需要反过来贪心地计算他长够高度需要的最短时间，然后判断能不能都满足。

最短时间仍然可以二分，计算比较简单，但要注意爆 long long 的问题。判断时，我们注意到由于每分钟都会种一棵树，所以总时间是 \(n\)，这样就可以枚举时间判断，如果需要在时间 \(i\) 之前种的树超过 \(i\) 个就不合法。

怎么表现树上限制呢？只需用孩子更新一下祖先即可。

需要注意 \(c_i\) 正负的讨论，列算式时也要小心。

#include<bits/stdc++.h>
#define eps 1e-10
#define INF 0x3f3f3f3f
#define rep(i, l, r) for(int i=(l); i<=(r); i++)
#define per(i, r, l) for(int i=(r); i>=(l); i--)
#define ls k<<1
#define rs k<<1|1
#define tmid ((tr[k].l+tr[k].r)>>1)
#define nmid ((l+r)>>1)
#define pub push_back
#define all(v) v.begin(), v.end()
#define pii pair<int, int>
#define mkp make_pair
#define x first
#define y second
using namespace std;
#define int long long
inline void Read(int &x){
  int f=1; x=0;
  char c=getchar();
  while(c<'0' || c>'9'){
    if(c=='-') f=-1;
    c=getchar();
  }
  while(c>='0' && c<='9'){
    x=(x<<3)+(x<<1)+c-'0', c=getchar();
  }
  x*=f;
}
const int N=1e5+10;
int n, a[N], b[N], c[N];
vector<int> e[N];
int ddl[N]; // i must be planted before ddl[i]
// x in [beg, ed], grow max(bi+x*ci, 1) a day
inline bool Calc(int ai, int bi, int ci, int beg, int ed){
  if(ci==0) return bi*(ed-beg+1)>=ai;
  if(ci>0){
    __int128 res=(__int128)(beg+ed)*(ed-beg+1)/2*ci;
    res+=(__int128)bi*(ed-beg+1);
    return res>=ai;
  }else {
    __int128 res=0;
    if(bi+beg*ci<=0) res=ed-beg+1;
    else if(bi+ed*ci>0) res=bi*(ed-beg+1)+(__int128)(beg+ed)*(ed-beg+1)/2*ci;
    else {
      int pos=(bi-1)/(-ci);
      res=bi*(pos-beg+1)+(__int128)(beg+pos)*(pos-beg+1)/2*ci+(ed-pos);
    }
    return res>=ai;
  }
}
void DFS(int u, int ff){
  for(int v: e[u]) if(v!=ff){
    DFS(v, u), ddl[u]=min(ddl[u], ddl[v]-1);
  }
}
int cnt[N];
bool Check(int tim){
  rep(i, 1, n){
    ddl[i]=0;
    int l=1, r=n;
    while(l<=r){
      int m=nmid;
      if(Calc(a[i], b[i], c[i], m, tim)) ddl[i]=m, l=m+1;
      else r=m-1;
    }
  }
  DFS(1, 0);
  rep(i, 1, n) if(ddl[i]<1) return 0;
  rep(i, 1, n) cnt[i]=0;
  rep(i, 1, n) cnt[ddl[i]]++;
  rep(i, 1, n){
    cnt[i]+=cnt[i-1];
    if(cnt[i]>i) return 0;
  }
  return 1;
}
signed main(){
  Read(n);
  rep(i, 1, n) Read(a[i]), Read(b[i]), Read(c[i]);
  rep(i, 2, n){
    int u, v; Read(u), Read(v);
    e[u].pub(v), e[v].pub(u);
  }
  int l=n, r=1e9, res=0;
  while(l<=r){
    int m=nmid;
    if(Check(m)) res=m, r=m-1;
    else l=m+1;
  }
  printf("%lld\n", res);
  return 0;
}