关于我第八天又抱灵了这档事

0.杂谈

过来之后没断网，不知道能苟到什么时候……
猫出题，打开一看又有字符串，直接报废。
尝试搜了一下样例，是 CF1063F

1.简易题解

A

题面见 CF722F。
对于每个 \(x\) 分别求解，问题即为关于时间 \(t\) 的 \(n\) 个同余方程的最长有解区间。
由于 \(k_i\le40\)，所以可以讨论 \(40\) 以内的每一个 \(p^a\)，维护模每个质数幂的限制。

B

题面见 CF1063F。
正解是 SAM？但是我显然不会，于是我们用哈希水这道题。
首先长度依次减一的性质很容易发现，然后又发现答案是 \(O(\sqrt{n})\) 级别的，那么可以考虑枚举这个答案。
然后考虑如何判定是否存在。可以从后往前枚举后缀 \(i\)，每次如果不重复就加入 \([i,i+ans-1]\) 这一段，然后查询是否存在 \([i+1,i+ans-1]\) 或 \([i,i+ans-2]\) 就行了。
每轮用到的哈希值是定长的，可以递推出来。由于出题人似乎没有刻意卡哈希，所以单哈希过了。

C

题面见 CF814E，二次加强后与原题面的区别是 \(n\le1000\)。
容易发现，这个图可以按照 BFS 树分层：

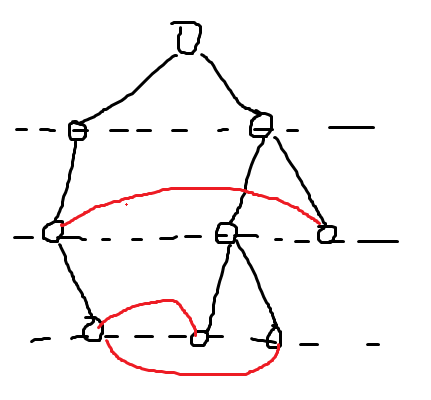
而 \(i\) 一定在 \(i-1\) 的同一层或下一层。
于是我们可以考虑按层 dp，设 \(f_{i,j,k}\) 为当前层 \(i\) 个点、上一层的二/三度点分别有 \(j,k\) 个。
转移方程如下：\(f_{i,j,k}=f_{i-1,j-1,k}\times j+f_{i-1,j+1,k-1}\times k\)。
方程的两部分分别表示连向了上一层的（原）一度点和二度点使它们变成二度点和三度点。
考虑 \(i=0\) 的情况，发现 \(f_{0,j,k}=f_{0,j-2,k}\times(j-1)+f_{0,j,k-1}\times k\)。
它表示的是平边的转移。
而 \(f_{0,0,k}=\sum\limits_{l=2}^{k-1}f_{0,0,k-l-1}\times\dbinom{k-1}l\times\dfrac{l!}2\)。
因为上层除去连上去的每个点连出了两条边，那么会形成环，我们枚举环的大小即可。
接下来考虑如何统计答案，设 \(g_{i,j}\) 表示枚举到第 \(i\) 个点、此时当前层有 \(j\) 个点的方案数。
那么 \(g_{i,j}=\sum\limits_{k=1}^{i-j}g_{i-j,k}f_{j,d,t}\)，其中 \(d,t\) 表示上一层的 \(k\) 个数中二/三度点的个数。
那么最终答案就是枚举最后一层的点 \(\sum\limits_{j=1}^{n-1}f_{0,d,t}g_{n,j}\)。
一次加强版的 \(n\le300\)，可以通过。
至于二次加强版，不会推式子，先咕着。

2.构造题选讲

1

题面见 AT4378。
构造方法是黑白染色，对于每个黑格所在主、副对角线放一个质数，空格子填上四周数字的 \(\text{lcm}+m\)。（\(m\) 随便选）
发现每个格子的数上界是很松的 \(10^{16}\)，调整一下可以通过。

2

构造方法：给每个拼图的两边赋值，使得值相同的能拼在一起。
这样我们将不同的值看作点，一块拼图看做边，现在需要将所有边划分为若干互不相交的路径，使得起点为正权、中点为负权，所以直接看度数就行了。
懒得写了