美好的第六天~不会做的题目~

0.杂谈

打开一看又是西江月，然后觉得自己要 WA 声一片/kk
看到了字符串，再次爆炸（赛后知道是论文题/jk）
T1 本来想硬推一下，但是脑力不足，然后又想部分分，状压一下发现假得不行（然后就没管了）
T3 空间限制 \(\text{8 MiB}\)，一看就很毒瘤，所以暴力滚蛋。
最终得分：\(0+0+0=0\)。

1.简易题解

A

题面见 CF838D。
类比 Parking 函数的处理方法，加一个物品合链成环。
每个人均匀随机一个方向和物品，方案数为 \(2^m(n+1)^m\)，而每个物品没有被拿走的概率都是 \(\dfrac{n-m+1}{n+1}\)，所以答案就是 \(2^m(n+1)^{m-1}(n-m+1)\)。考场上我这个傻逼没发现可以用概率做，所以说我自裁。

B

给出两个长度相同的 AGCT 字符串 \(S,T\)，求最长公共循环同构子序列。
实际上是求 \(S+S\) 的全体长度为 \(n\) 的子串与 \(T\) 的 LCS 最大值。
有一篇论文提到了它的 \(O(n^2)\) 做法（对于长度不相同的串是 \(O(nm)\)）。
先考虑如何求普通 LCS，我们把 dp 方程写成有向图的形式：

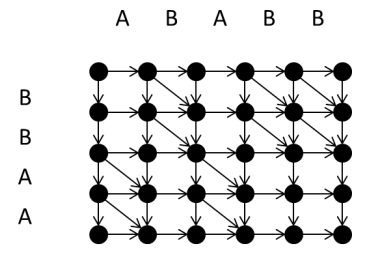
最后的答案就是这样的：

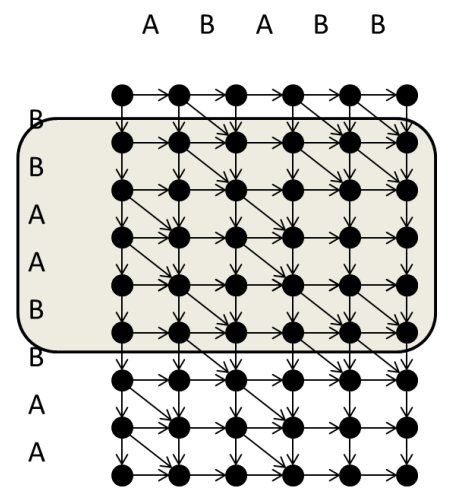
记 \(f_{i,j,k}=\text{LCS}(S[i,j],T[1,k])\)，那么由图显然有 \(f_{i-1,j,k}>f_{i-1,j-1,k}\Rightarrow f_{i,j,k}>f_{i,j-1,k}\)。
同理，\(f_{i,j,k}>f_{i,j,k-1}\Rightarrow f_{i-1,j,k}>f_{i-1,j,k-1}\)。
所以存在分界点 \(p_{k,j}\) 和 \(q_{k,j}\) 使得 \(f_{i,j,k}=f_{i,j-1,k}+[i\ge p_{k,j}]=f_{i,j,k-1}+[i<q_{k,j}]\)。
当 \(S_j\ne T_k\) 时，记 \(F=f_{i,j-1,k-1},P=p_{k-1,j},Q=q_{k,j-1}\)，那么若 \(P<Q\) 则 \(p_{k,j}=Q,q_{k,j}=P\)；若 \(P\ge Q\)，则 \(p_{k,j}=P,q_{k,j}=Q\)。
当 \(S_j=T_k\) 时，\(f_{i,j,k}=F+1\)，此时 \(p_{k,j}=Q,q_{k,j}=P\)。
借用老师的两张图：


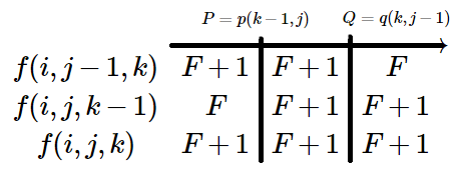
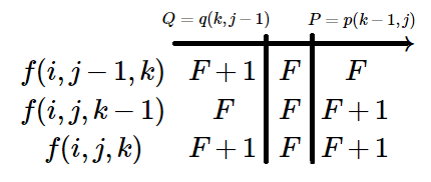
边界条件是 \(p_{0,j}=j+1,q_{0,j}=1\)，然后就可以递推出答案了。
但是并没有搞很懂，所以上面可能摘抄的有些问题（

C

题面见 LOJ6499。
考虑压位暴力。整块压位查一次 \(O\left(\dfrac nw\right)\)，散块直接查，可以取块长 \(\dfrac nw\)。
然后空间就炸了，但是我们可以用 st 表解决。
然后时间又炸了，考虑如何卡常。注意到只出现一次的数可以前缀和统计，然后有效值的种类数就下降到 \(\dfrac n2\)，可以通过。

2.不定方程与积性函数

1

题面见洛谷 P3306。
\(x_n\equiv x_0\pmod m\) 等价于 \(m|(a^n-1)x_0+b(1+a+\dots+a^{n-1})\)，\(a\ne1\) 时等价于 \((a-1)m|(a^n-1)((a-1)x_0+b)\)。
令 \(A=(a-1)m,B=(a-1)x_0+b\)，那么有 \(a^n\equiv1\pmod{\frac{A}{\gcd(A,B)}}\)，于是就可以解了。
需要注意特判。

2

设 \(f\) 为斐波那契数列，多次查询，每次给定 \(p,x\)，求最小正整数 \(n\) 使得 \(f_n\equiv x\pmod p\)。其中 \(p\equiv\pm1\pmod{10}\) 且 \(p\) 为质数。
发现 \(5\) 有二次剩余，所以直接写通项 \(x=f_n=\dfrac{1}{\sqrt{5}}\left(\phi^n-\hat{\phi}^n\right)\)，其中 \(\hat{\phi}=-\dfrac{1}{\phi}\)。
整理得 \((\phi^n)^2-\sqrt{5}x\phi^n-(-1)^n\equiv0\pmod p\)，即 \(\phi^n=\dfrac{\sqrt{5}x\pm\sqrt{5x^2+4(-1)^n}}{2}\)。
讨论 \(n\) 的奇偶性，然后二次剩余+离散对数就行了。

3

一个 \(r\times c\) 的矩形房间，从一角沿角平分线发射一束光，设光第一次反射到角落前的碰壁次数为 \(f_{r,c}\)，求 \(\sum_{r=1}^m\sum_{c=1}^nf_{r,c}\)。
把房间扩充，那么反射可以看成穿过，则 \(f_{r,c}=\dfrac{\text{lcm}(r,c)}{R}+\dfrac{\text{lcm}(r,c)}{c}-2=\dfrac{r+c}{\gcd(r,c)}-2\)。
所以暴力碾式子（以下设 \(m\le n\)）：

\[\begin{aligned} &\sum_{r=1}^m\sum_{c=1}^n(\dfrac{r+c}{\gcd(r,c)}-2)\\ =&-2mn+\sum_{d=1}^m\sum_{r=1}^m\sum_{c=1}^n[\gcd(r,c)=d]\dfrac{r+c}{d}\\ =&-2mn+\sum_{d=1}^m\sum_{i=1}^{\lfloor m/d\rfloor}\sum_{j=1}^{\lfloor n/d\rfloor}[\gcd(i,j)=1](i+j)\\ =&-2mn+\sum_{d=1}^m\sum_{i=1}^{\lfloor m/d\rfloor}\sum_{j=1}^{\lfloor n/d\rfloor}\sum_{t|\gcd(i,j)}\mu(t)(i+j)\\ =&-2mn+\sum_{d=1}^m\sum_{t=1}^{\lfloor m/d\rfloor}\mu(t)\sum_{i=1}^{\lfloor m/dt\rfloor}\sum_{j=1}^{\lfloor n/dt\rfloor}t(i+j)\\ =&-2mn+\sum_{d=1}^m\sum_{t|d}t\mu(t)\sum_{i=1}^{\lfloor m/d\rfloor}\sum_{j=1}^{\lfloor n/d\rfloor}(i+j)\\ =&-2mn+\sum_{d=1}^m\sum_{t|d}t\mu(t)\dfrac{\lfloor m/d\rfloor\lfloor n/d\rfloor(\lfloor m/d\rfloor+\lfloor n/d\rfloor-2)}{2} \end{aligned} \]

，碾完之后发现 \(\sum\limits_{t|d}t\mu(t)\) 是积性函数，线性筛处理出来后整除分块。